欧拉函数模板一:
求一个数的欧拉函数
ll Eoula(int n) { ll res = n; for (ll i = 2; i*i <= n; i++) { if (n % i == 0) { res = res / i * (i - 1);//先除防止数据溢出 while (n % i == 0)n /= i; } } if (n > 1)res = res / n * (n - 1); return res; }
欧拉函数模板二:
打表法:
const int maxn=1e6+100; const int mod=1000000007; int ol[maxn],prime[maxn],cnt=0; void oula(){//打表oula函数 ol[1]=1; for(int i=2;i<=42768;i++){ if(!ol[i]){ ol[i]=i-1; prime[++cnt]=i; } for(int j=1;j<=cnt&&i*prime[j]<=42768;j++){ if(i%prime[j]){ ol[i*prime[j]]=ol[i]*(prime[j]-1); } else{ ol[i*prime[j]]=ol[i]*prime[j]; break; } } } }
A题:找新朋友
A题就是一个模板题,就是求n的欧拉函数值
AC代码:

#pragma GCC optimize(1) #pragma GCC optimize(2) #pragma GCC optimize(3,"Ofast","inline") #include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<algorithm> using namespace std; typedef long long ll; template <typename Tp> void read(Tp &x){//read(n); x=0;char ch=1;int fh; while(ch!='-'&&(ch>'9'||ch<'0')){ ch=getchar(); } if(ch=='-'){ fh=-1;ch=getchar(); }else fh=1; while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+ch-'0';ch=getchar(); } x*=fh; } inline char read1()//字符串读入挂 { register char ch=getchar(); while(ch<'A'||ch>'M')ch=getchar(); return ch; } const int maxn=1e6+100; const int mod=1000000007; int ol[maxn],prime[maxn],cnt=0; int n; void oula(){ ol[1]=1; for(int i=2;i<=42768;i++){ if(!ol[i]){ ol[i]=i-1; prime[++cnt]=i; } for(int j=1;j<=cnt&&i*prime[j]<=42768;j++){ if(i%prime[j]){ ol[i*prime[j]]=ol[i]*(prime[j]-1); } else{ ol[i*prime[j]]=ol[i]*prime[j]; break; } } } } int main(){ oula(); int t; cin>>t; while(t--){ int n; cin>>n; cout<<ol[n]<<endl; } }
题目大意就是输入一个n求gcd(n,m)>1的m的个数,就是用n-oula(n)-1;

#pragma GCC optimize(1) #pragma GCC optimize(2) #pragma GCC optimize(3,"Ofast","inline") #include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<algorithm> using namespace std; typedef long long ll; template <typename Tp> void read(Tp &x){//read(n); x=0;char ch=1;int fh; while(ch!='-'&&(ch>'9'||ch<'0')){ ch=getchar(); } if(ch=='-'){ fh=-1;ch=getchar(); }else fh=1; while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+ch-'0';ch=getchar(); } x*=fh; } inline char read1()//字符串读入挂 { register char ch=getchar(); while(ch<'A'||ch>'M')ch=getchar(); return ch; } const int maxn=1e6+100; const int mod=1000000007; int ol[maxn],prime[maxn],cnt=0; void oula(){//打表oula函数 ol[1]=1; for(int i=2;i<=42768;i++){ if(!ol[i]){ ol[i]=i-1; prime[++cnt]=i; } for(int j=1;j<=cnt&&i*prime[j]<=42768;j++){ if(i%prime[j]){ ol[i*prime[j]]=ol[i]*(prime[j]-1); } else{ ol[i*prime[j]]=ol[i]*prime[j]; break; } } } } ll Eoula(int n) {//求φ(m/tmp) ll res = n; for (ll i = 2; i*i <= n; i++) { if (n % i == 0) { res = res / i * (i - 1);//先除防止数据溢出 while (n % i == 0)n /= i; } } if (n > 1)res = res / n * (n - 1); return res; } int main(){ ll n; while(cin>>n&&n){ ll sum=Eoula(n); cout<<n-sum-1<<endl; } }
求给定一个正整数N,计算小于N且与 N不互质的正整数之和。
若(a,n)=1,则(n−a,n)=1
证明:
(a,n)=(n−a,a)=(n−a,n)(a,n)=(n−a,a)=(n−a,n)(更相减损法)
由于gcd ( a , n ) = gcd ( n − a , n ) ,这说明不互质的数是成对出现的,且一对的和为n / 2,那么答案就是: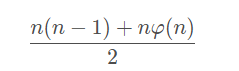

#pragma GCC optimize(1) #pragma GCC optimize(2) #pragma GCC optimize(3,"Ofast","inline") #include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<algorithm> using namespace std; typedef long long ll; template <typename Tp> void read(Tp &x){//read(n); x=0;char ch=1;int fh; while(ch!='-'&&(ch>'9'||ch<'0')){ ch=getchar(); } if(ch=='-'){ fh=-1;ch=getchar(); }else fh=1; while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+ch-'0';ch=getchar(); } x*=fh; } inline char read1()//字符串读入挂 { register char ch=getchar(); while(ch<'A'||ch>'M')ch=getchar(); return ch; } const int maxn=1e6+100; const int mod=1000000007; int ol[maxn],prime[maxn],cnt=0; void oula(){//打表oula函数 ol[1]=1; for(int i=2;i<=42768;i++){ if(!ol[i]){ ol[i]=i-1; prime[++cnt]=i; } for(int j=1;j<=cnt&&i*prime[j]<=42768;j++){ if(i%prime[j]){ ol[i*prime[j]]=ol[i]*(prime[j]-1); } else{ ol[i*prime[j]]=ol[i]*prime[j]; break; } } } } ll Eoula(int n) {//求φ(m/tmp) ll res = n; for (ll i = 2; i*i <= n; i++) { if (n % i == 0) { res = res / i * (i - 1);//先除防止数据溢出 while (n % i == 0)n /= i; } } if (n > 1)res = res / n * (n - 1); return res; } int main(){ ll n; //3 1 2 //4 1 2 3 while(cin>>n&&n){ ll ans=1ll*n*(n-1)/2-n*Eoula(n)/2; cout<<ans%mod<<endl; } }
就是求[a,b]之间的欧拉函数之和,打表法可以求

#pragma GCC optimize(1) #pragma GCC optimize(2) #pragma GCC optimize(3,"Ofast","inline") #include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<algorithm> using namespace std; typedef long long ll; template <typename Tp> void read(Tp &x){//read(n); x=0;char ch=1;int fh; while(ch!='-'&&(ch>'9'||ch<'0')){ ch=getchar(); } if(ch=='-'){ fh=-1;ch=getchar(); }else fh=1; while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+ch-'0';ch=getchar(); } x*=fh; } inline char read1()//字符串读入挂 { register char ch=getchar(); while(ch<'A'||ch>'M')ch=getchar(); return ch; } const int maxn=5e6+100; const int mod=1000000007; int ol[maxn],prime[maxn],cnt=0; void oula(){//打表oula函数 ol[1]=1; for(int i=2;i<=3000110;i++){ if(!ol[i]){ ol[i]=i-1; prime[++cnt]=i; } for(int j=1;j<=cnt&&i*prime[j]<=3000110;j++){ if(i%prime[j]){ ol[i*prime[j]]=ol[i]*(prime[j]-1); } else{ ol[i*prime[j]]=ol[i]*prime[j]; break; } } } } ll Eoula(int n) {//求φ(m/tmp) ll res = n; for (ll i = 2; i*i <= n; i++) { if (n % i == 0) { res = res / i * (i - 1);//先除防止数据溢出 while (n % i == 0)n /= i; } } if (n > 1)res = res / n * (n - 1); return res; } int main(){ int a,b; oula(); while(cin>>a>>b){ ll ans=0; for(int i=a;i<=b;i++){ ans+=ol[i]; } cout<<ans<<endl; } }
E题:E - GCD
题意:给定整数N和M,多少整数X满足1 <= X <= N和gcd(X,N)> = M。
假设X和N的最大公约数为d
gcd(N,X)>=m
gcd(p*d,q*d)>=m
所以p和q是互质的
所以就是找满足N=p*d,并且d>=m的p的欧拉函数之和(sqrt(N)的复杂度可以求)

#pragma GCC optimize(1) #pragma GCC optimize(2) #pragma GCC optimize(3,"Ofast","inline") #include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<algorithm> using namespace std; typedef long long ll; template <typename Tp> void read(Tp &x){//read(n); x=0;char ch=1;int fh; while(ch!='-'&&(ch>'9'||ch<'0')){ ch=getchar(); } if(ch=='-'){ fh=-1;ch=getchar(); }else fh=1; while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+ch-'0';ch=getchar(); } x*=fh; } inline char read1()//字符串读入挂 { register char ch=getchar(); while(ch<'A'||ch>'M')ch=getchar(); return ch; } const int maxn=1e6+100; const int mod=1000000007; int ol[maxn],prime[maxn],cnt=0; int n; void oula(){//打表oula函数 ol[1]=1; for(int i=2;i<=42768;i++){ if(!ol[i]){ ol[i]=i-1; prime[++cnt]=i; } for(int j=1;j<=cnt&&i*prime[j]<=42768;j++){ if(i%prime[j]){ ol[i*prime[j]]=ol[i]*(prime[j]-1); } else{ ol[i*prime[j]]=ol[i]*prime[j]; break; } } } } int Eoula(int n) {//求φ(m/tmp) int res = n; for (int i = 2; i*i <= n; i++) { if (n % i == 0) { res = res / i * (i - 1);//先除防止数据溢出 while (n % i == 0)n /= i; } } if (n > 1)res = res / n * (n - 1); return res; } int main(){ //假设他的最大公约数为d //gcd(n,x)>=m //gcd(p*d,q*d)>=m //所以p和q是互质的 //所以就是找满足n=p*d,并且d>=m的p的欧拉函数之和 int t; cin>>t; while(t--){ int n,m; cin>>n>>m; int ans=0; for(int i=1;i*i<=n;i++){ if(n%i==0){ if(i>=m){ ans+=Eoula(n/i); } if((n/i)>=m&&(n/i)!=i){ ans+=Eoula(i); } } } cout<<ans<<endl; } }
原根个数
给定一个奇素数,求他的原根的个数,其中,一个数n的原根是指一个小于n的正整数x,若有x^1mod n,x^2 mod n...x^n-1 mod n刚好是n-1的一个全排列,
那么就称x是n的一个原根。
解题思路:这里用到了两个定理,第一个是奇素数一定有原根,第二个是一个数n的原根的个数ans=euler(euler(n)),由于是一个奇素数,因此ans=euler(n-1)。

#pragma GCC optimize(1) #pragma GCC optimize(2) #pragma GCC optimize(3,"Ofast","inline") #include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<algorithm> using namespace std; typedef long long ll; template <typename Tp> void read(Tp &x){//read(n); x=0;char ch=1;int fh; while(ch!='-'&&(ch>'9'||ch<'0')){ ch=getchar(); } if(ch=='-'){ fh=-1;ch=getchar(); }else fh=1; while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+ch-'0';ch=getchar(); } x*=fh; } inline char read1()//字符串读入挂 { register char ch=getchar(); while(ch<'A'||ch>'M')ch=getchar(); return ch; } const int maxn=1e6+100; const int mod=1000000007; int ol[maxn],prime[maxn],cnt=0; void oula(){//打表oula函数 ol[1]=1; for(int i=2;i<=42768;i++){ if(!ol[i]){ ol[i]=i-1; prime[++cnt]=i; } for(int j=1;j<=cnt&&i*prime[j]<=42768;j++){ if(i%prime[j]){ ol[i*prime[j]]=ol[i]*(prime[j]-1); } else{ ol[i*prime[j]]=ol[i]*prime[j]; break; } } } } ll Eoula(int n) {//求φ(m/tmp) ll res = n; for (ll i = 2; i*i <= n; i++) { if (n % i == 0) { res = res / i * (i - 1);//先除防止数据溢出 while (n % i == 0)n /= i; } } if (n > 1)res = res / n * (n - 1); return res; } int main(){ ll n; while(cin>>n&&n){ cout<<Eoula(n-1)<<endl; } }
