gcd和lcm在分解质因子的应用

lcm:

传送门

找到以下代码的结果:

long long pairsFormLCM( int n ) {
    long long res = 0;
    for( int i = 1; i <= n; i++ )
        for( int j = i; j <= n; j++ )
           if( lcm(i, j) == n ) res++; // lcm means least common multiple
    return res;
}

代码的直接实现可能会超时。如果您分析代码，您将发现代码实际上计数lcm(i, j) = n和(i≤j)的对(i, j)的数量。

输入

输入以整数T(≤200)开始，表示测试用例的数量。

每一种情况都以包含整数n(1≤n≤1014)的行开始。

输出

对于每种情况，打印大小写和函数'pairsFormLCM(n)'返回的值

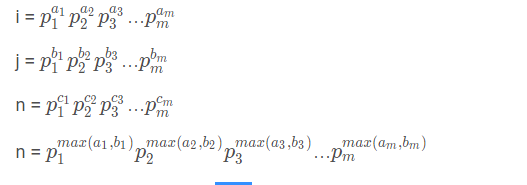
 lcm是max(a1,b1)的最大值，gcd是最小值min(a1,b1）

上面是lcm 的性质。 现在考虑怎么计算。
因为lcm是质因子的指数取max，那么也就是说。
对于某一个质因子px i,j里面 必然有一个指数要等于 n的指数 也就是cx。 另外一个呢,[0-cx] 任选一个都行，总共cx+1 种可能。
那么如果不考虑，i，j 的大小，即 j 可以小于 i，那么对于这一个质因子，方案数就是2*cx+1。

对于其中的一项pi^ai来说，选择的两个数之一必须包含它，另外一个随意。。

对于 ai == ei 时候， bi 可取 [0 ei] 共 1+ei 个情况

ai < ei 时 bi 只可取 ei , ai 可取 [0, ei) 共  ei 个情况

合起来共有 2ei+1 

都取max(a,b) 的时候算了1次，而且ab ba是一种情况，所以我们还需要 +1之后再/2（先/2的话会默认向下取整出现问题）

答案就显而易见了。

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll; 
const int maxn=1e7+100;
bool biaoji[maxn];
int prime[maxn/10];
int cnt=0; 
void inint(){
    for(int i=2;i<maxn;i++){
        if(!biaoji[i]) prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){
            biaoji[i*prime[j]]=1;
            if(i%prime[j]==0){
                break;
            } 
        }
    }
}
ll n;
ll t;
int main(){
    cin>>t;
    inint();
    int kase=1;
    while(t--){    
        scanf("%lld",&n);
        ll ans=1;
        for(int i=1;i<=cnt;i++){
            if(1ll*prime[i]*prime[i]>n){
                break;
            }
            ll p=0;
            while(n%prime[i]==0){
                n/=prime[i];
                p++;
            }
            if(p){ 
                ans*=(p*2+1); 
            } 
        }
        if(n>1){
            ans*=3;
        }
        printf("Case %d: %lld
",kase++,(ans+1)/2);
    }
}

​gcd

传送门

求满足条件的最大的指数p，使得a^p = x（a是整数）

Input

输入包含多组样例T（T<=50），每个样例包括一个整数x，x的范围在32位二进制数以内, 保证x的绝对值大于等于2。

Output

对于每个样例输出最大的指数p。

Sample Input

3

17

1073741824

25

Sample Output

Case 1: 1

Case 2: 30

Case 3: 2

x = p1^x1*p2^x2*p3^x3*...*ps^xs

x = b^p, x只有一个因子的p次幂构成

如果x = 12 = 2^2*3^1，要让x = b^p,及12应该是12 = 12^1

所以p = gcd(x1, x2, x3, ... , xs);

比如：24 = 2^3*3^1，p应该是gcd(3, 1) = 1,即24 = 24^1

         324 = 3^4*2^2,p应该是gcd(4, 2) = 2,即324 = 18^2

本题有一个坑，就是x可能为负数，如果x为负数的话，x = b^q, q必须使奇数，所以将x转化为正数求得的解如果是偶数的话必须将其一直除2转化为奇数

求x=bp中最大的p,x可能为负数。

因数分解，x=p1x1*p2x2*...*pnxn

                  x=(p1x1‘*p2x2‘*...*pnxn‘)q

  如果x是正数的话，那么这个q最大就是gcd(x1,x2...xn),也就是答案了。

  如果x是负数，那么q显然应该是个奇数，让求得的q不断/2直至为奇数即可。

  题目明明说了x的范围在32为之内搞不懂为什么开LL才能过c。

代码：

#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e5+100;
bool biaoji[maxn];
int prime[maxn];
int cnt=0; 
int p[maxn];
int c[maxn];
void inint(){
    for(int i=2;i<maxn;i++){
        if(!biaoji[i]) prime[++cnt]=i;
        for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){
            biaoji[i*prime[j]]=1;
            if(i%prime[j]==0){
                break;
            }
        } 
    }
}
int gcd(int a,int b){
    if(b==0){
        return a;
    }
    else{
        return gcd(b,a%b);
    }
} 
int main(){
    int t;
    ll n;//注意开ll因为负数会爆 
    inint();
    cin>>t;
    int kase=1;
    while(t--){
        cin>>n;
        int flag=0;
        if(n<0){
            flag=1;
            n=-n;
        }
        int cot=0;
        for(ll i=1;i<=cnt&&prime[i]*prime[i]<=n;i++){
            if(n%prime[i]==0){
                c[++cot]=0; 
                p[cot]=i;
                while(n%prime[i]==0){
                    c[cot]++;
                    n/=prime[i];
                }
            } 
        }
        if(n>1){
            c[++cot]=1;
            p[cot]=n;
        }
        int ans=c[1];
        for(int i=2;i<=cot;i++){
            ans=gcd(ans,c[i]);
        } 
        if(flag){
            while(ans%2==0){
                ans>>=1;
            }
        }
        printf("Case %d: %d
",kase++,ans);
    }
}