问题 A: 面积 (area)
编程计算在一个10*10的网格中,由 * 号围成的下列图形的面积。面积计算方法是统计 * 号所围成的闭合曲线中水平线和垂直线交点的数目。



如下图所示,在10*10的二维数组中,有 * 围住了15点,因此面积为15。


输入
一个10*10的网格。同行元素间用空格隔开。
1表示 *。
1表示 *。
输出
输出一个整数,表示答案。
样例输入 Copy
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 0 0 0
0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 1 0 0 1 0
0 0 1 0 0 0 1 0 1 0
0 1 0 1 0 1 0 0 1 0
0 1 0 0 1 1 0 1 1 0
0 0 1 0 0 0 0 1 0 0
0 0 0 1 1 1 1 1 0 0
0 0 0 0 0 0 0 0 0 0
样例输出 Copy
15
就是一个BFS;
#include<cstdio> #include<iostream> #include<algorithm> #include<map> #include <math.h> #include<bits/stdc++.h> using namespace std; typedef long long ll; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } const int INF=0x3f3f3f3f; const int maxn=1e5+100; int a[200][200]; struct node{ int x,y; }; int nx[4]={0,0,1,-1}; int ny[4]={1,-1,0,0}; void inint(){ for(int i=1;i<=10;i++){ for(int j=1;j<=10;j++){ cin>>a[i][j]; } } } void bfs(int u,int v){ queue<node>q; node temp,next; temp.x=u,temp.y=v; q.push(temp); while(!q.empty()){ temp=q.front(); for(int i=0;i<4;i++){ next.x=temp.x+nx[i]; next.y=temp.y+ny[i]; if(next.x>=0&&next.x<=11&&next.y>=0&&next.y<=11&&a[next.x][next.y]==0){ a[next.x][next.y]=1; q.push(next); } } q.pop(); } } int main(){ inint(); bfs(0,0); int num=0; for(int i=0;i<=11;i++){//扩大边界防止边界有1,使得队列停止 for(int j=0;j<=11;j++){ if(a[i][j]==0){ num++; } } } printf("%d",num); }
问题 B: 营救 (save)
这是一个BFS计数(板子题)
铁塔尼号遇险了!他发出了求救信号。距离最近的哥伦比亚号收到了讯息,时间就是生命,必须尽快赶到那里。
通过侦测,哥伦比亚号获取了一张海洋图。这张图将海洋部分分化成n*n个比较小的单位,其中用1标明的是陆地,用0标明是海洋。船只能从一个格子,移到相邻的四个格子。
为了尽快赶到出事地点,哥伦比亚号最少需要走多远的距离。
#include<iostream> #include<algorithm> #include<queue> using namespace std; typedef long long ll; const int maxn=1e3+100; int vis[maxn][maxn]; char a[maxn][maxn]; struct node{ int x; int y; int st; }; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; int n,sx,sy,ex,ey; int bfs(int x,int y){ queue<node>q; node no,nx; no.x=x; no.y=y; no.st=0; q.push(no); while(!q.empty()){ no=q.front(); q.pop(); for(int i=0;i<4;i++){ nx.x=no.x+dx[i]; nx.y=no.y+dy[i]; nx.st=no.st+1; if(nx.x<=0||nx.y<=0||nx.x>n||nx.y>n||a[nx.x][nx.y]=='1'||vis[nx.x][nx.y]==1)continue; vis[nx.x][nx.y]=1; if(nx.x==ex&&nx.y==ey){ return nx.st; } q.push(nx); } } } int main(){ cin>>n; for(int i=1;i<=n;i++){ scanf("%s",a[i]+1); } cin>>sx>>sy>>ex>>ey; int t=bfs(sx,sy); printf("%d ",t); }
问题 C: 最少转弯问题 (turn)
给出一张地图,这张地图被分为n*m(n,m≤100)个方块,任何一个方块不是平地就是高山。平地可以通过,高山则不能。现在你处在地图的(x1,y1)这块平地,问:你至少需要拐几个弯才能到达目的地(x2,y2)?你只能沿着水平和垂直方向的平地上行进,拐弯次数就等于行进方向的改变(从水平到垂直或从垂直到水平)的次数。例如:如图 8-6,最少的拐弯次数为5。
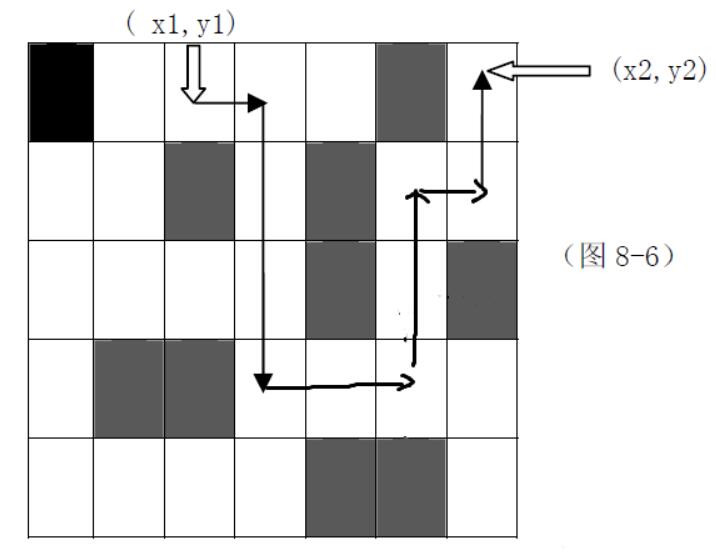
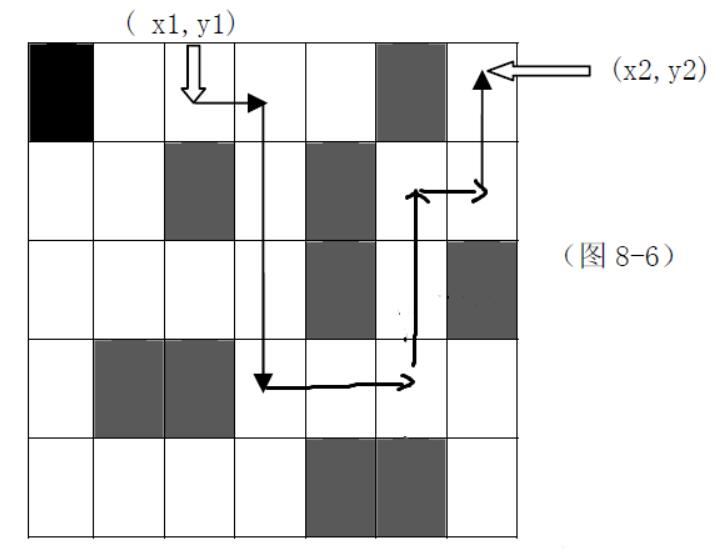


输入
输入将遵循以下格式:


a数组为整个地图地形描述(0:空地;1:高山)。


a数组为整个地图地形描述(0:空地;1:高山)。
样例输入 Copy
5 7
1 0 0 0 0 1 0
0 0 1 0 1 0 0
0 0 0 0 1 0 1
0 1 1 0 0 0 0
0 0 0 0 1 1 0
1 3 1 7
样例输出 Copy
5
就是拐一次弯之后,把这个方向上的点都标记上
这是我的代码
#include<iostream> #include<algorithm> #include<queue> using namespace std; const int maxn=5e3+100; char a[maxn][maxn]; int vis[maxn][maxn]; int dx[4]={0,0,1,-1}; int dy[4]={1,-1,0,0}; struct node{ int x,y,t; }; int n,m,sx,sy,ex,ey; int ans=0x3f3f3f; int f=0; void BFS(){ queue<node>q; node tmp,nxt; tmp.x=sx,tmp.y=sy,tmp.t=-1;//因为第一步不算 vis[tmp.x][tmp.y]=1; q.push(tmp); while(!q.empty()){ tmp=q.front(); q.pop(); nxt.t=tmp.t+1; for(int i=0;i<4;i++){//相当于拐了一次弯 int xx=tmp.x,yy=tmp.y; while(1){//把这一个方向的都标记了 xx=xx+dx[i],yy=yy+dy[i]; if(xx<0||xx>=n||yy<0||yy>=m){ break; } if(a[xx][yy]=='1') break; if(vis[xx][yy]) break; vis[xx][yy]=1; nxt.x=xx,nxt.y=yy; if(xx==ex&&yy==ey){ f=1; ans=min(ans,nxt.t); return ; } q.push(nxt); } } } } int main(){ cin>>n>>m>>sx>>sy>>ex>>ey; for(int i=0;i<n;i++){ scanf("%s",a[i]); } BFS(); if(f){ cout<<ans<<endl; } else{ cout<<-1<<endl; } }
问题 F: Heartlessly 的三角形
Heartlessly有一个填满了数字的三角形。这个三角形一共有n层,其中第i层共有i个数,且第1个数和第i个数均为i。其余的数中,第j个数是上一层中第j−1个数和第j个数的和。请你求出Heartlessly的三角形中第x层到第y层所有数的和,对1e9+7取模,一共有m个询问。
输入
第一行,输入两个正整数n,m,表示三角形的层数和询问个数。
接下来m行,每行两个正整数x,y,表示一次询问。
接下来m行,每行两个正整数x,y,表示一次询问。
输出
共m行,每行一个整数,表示每组询问的答案,对1e9+7取模。
样例输入 Copy
5 3
1 2
1 5
3 5
样例输出 Copy
5
83
78
提示
样例解释
当 n = 5 时,Heartlessly 的三角形为:
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5
对于 45% 的数据,n, m ≤ 1e3 ;
对于 70% 的数据,n ≤ 1e3 ;
对于 95% 的数据,n ≤ 1e5 ;
对于 100% 的数据,n ≤ 1e18 , m ≤ 105 , 1 ≤ x ≤ y ≤ n 。
当 n = 5 时,Heartlessly 的三角形为:
1
2 2
3 4 3
4 7 7 4
5 11 14 11 5
对于 45% 的数据,n, m ≤ 1e3 ;
对于 70% 的数据,n ≤ 1e3 ;
对于 95% 的数据,n ≤ 1e5 ;
对于 100% 的数据,n ≤ 1e18 , m ≤ 105 , 1 ≤ x ≤ y ≤ n 。
N很大
所以要找规律(其实是通过oeis),前N行的和为3*(2^n-1) - 2*n
通过前缀和的思想
#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int mod=1e9+7; ll qpow(ll a,ll b){ ll ans=1; while(b){ if(b&1){ ans=(ans*a)%mod; } a=(a*a)%mod; b/=2; } return ans; } //3*(2^n-1) - 2*n. int main(){ ll n,m; ll a,b; cin>>n>>m; while(m--){ scanf("%lld%lld",&a,&b); a--; ll ans1=((3*(qpow(2,b)-1)%mod)%mod+mod-(2*b)%mod)%mod; ll ans2=((3*(qpow(2,a)-1)%mod)%mod+mod-(2*a)%mod)%mod; printf("%lld ",(ans1-ans2+mod)%mod); } }
问题 G: Heartlessly 的魔法石
Heartlessly 有 n 个魔法石,每个魔法石都有对应的魔法值(用正整数 a i 表示)。Heartlessly把它们按魔法值从小到大排成一行,并分成 k 组,每组魔法石产生的能量为组中最大的魔法值减去最小的魔法值。你能求出这些魔法石产生的最小能量和最大能量分别是多少吗?
输入
第一行,输入两个正整数n,k,分别表示魔法石数量和分组数量。
第二行,输入正整数a1∼an,表示每个魔法石对应的魔法值。
第二行,输入正整数a1∼an,表示每个魔法石对应的魔法值。
输出
第一行,输出最小能量和最大能量,中间用空格隔开。
样例输入 Copy
8 3
2 3 5 7 11 13 17 19
样例输出 Copy
9 14
提示
样例解释
最小值:[2,3,5,7],[11,13],[17,19]
最大值:[2],[3,5],[7,11,13,17,19]
对于40%的数据,n≤15,ai≤100;
对于70%的数据,n≤103,ai≤106;
对于另外10%的数据,k=1;
对于另外10%的数据,k=n;
对于100%的数据,k≤n≤105,ai≤109,保证ai单调不减。
最小值:[2,3,5,7],[11,13],[17,19]
最大值:[2],[3,5],[7,11,13,17,19]
对于40%的数据,n≤15,ai≤100;
对于70%的数据,n≤103,ai≤106;
对于另外10%的数据,k=1;
对于另外10%的数据,k=n;
对于100%的数据,k≤n≤105,ai≤109,保证ai单调不减。
这个题其实很简单就是把差值找出来,如果要分成m端,所以要删除m-1个
只需要把差值排个序,输出最大值的时候只需要删除差值的最小的m-1个,然后把剩下的加起来
输出最小的时候只需要删除最大的m-1个,让后把剩下的加起来
#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1e6+1000; ll a[maxn]; ll b[maxn]; int main(){ int n,m; cin>>n>>m; for(int i=1;i<=n;i++){ cin>>a[i]; } for(int i=2;i<=n;i++){ b[i-1]=(a[i]-a[i-1]); } sort(b+1,b+n); int nn=n-1; int z=m-1; ll ans1=0; ll ans2=0; for(int i=z+1;i<=nn;i++){ ans1+=b[i]; } for(int i=1;i<=nn-z;i++){ ans2+=b[i]; } cout<<ans2<<" "<<ans1<<endl; }
问题 E: 优秀的拆分
一般来说,一个正整数可以拆分成若干个正整数的和。例如,1=1,10=1+2+3+4等。
对于正整数n的一种特定拆分,我们称它为“优秀的”,当且仅当在这种拆分下,n被分解为了若干个不同的2的正整数次幂。注意,一个数x能被表示成2的正整数次幂,当且仅当x能通过正整数个2相乘在一起得到。
例如,10=8+2=23+21是一个优秀的拆分。但是,7=4+2+1=22+21+20就不是一个优秀的拆分,因为1不是2的正整数次幂。
现在,给定正整数n,你需要判断这个数的所有拆分中,是否存在优秀的拆分。若存在,请你给出具体的拆分方案。
对于正整数n的一种特定拆分,我们称它为“优秀的”,当且仅当在这种拆分下,n被分解为了若干个不同的2的正整数次幂。注意,一个数x能被表示成2的正整数次幂,当且仅当x能通过正整数个2相乘在一起得到。
例如,10=8+2=23+21是一个优秀的拆分。但是,7=4+2+1=22+21+20就不是一个优秀的拆分,因为1不是2的正整数次幂。
现在,给定正整数n,你需要判断这个数的所有拆分中,是否存在优秀的拆分。若存在,请你给出具体的拆分方案。
输入
输入只有一行,一个正整数n,代表需要判断的数。
输出
如果这个数的所有拆分中,存在优秀的拆分。那么,你需要从大到小输出这个拆分中的每一个数,相邻两个数之间用一个空格隔开。可以证明,在规定了拆分数字的顺序后,该拆分方案是唯一的。
若不存在优秀的拆分,输出“-1”(不包含双引号)。
若不存在优秀的拆分,输出“-1”(不包含双引号)。
样例输入 Copy
【样例1】
6
【样例2】
7
样例输出 Copy
【样例1】
4 2
【样例2】
-1
提示
样例1解释
6=4+2=22+21是一个优秀的拆分。注意,6=2+2+2不是一个优秀的拆分,因为拆分成的3个数不满足每个数互不相同。
对于20%的数据,n≤10。
对于另外20%的数据,保证n为奇数。
对于另外20%的数据,保证n为2的正整数次幂。
对于80%的数据,n≤1024。
对于100%的数据,1≤n≤1×107。
6=4+2=22+21是一个优秀的拆分。注意,6=2+2+2不是一个优秀的拆分,因为拆分成的3个数不满足每个数互不相同。
对于20%的数据,n≤10。
对于另外20%的数据,保证n为奇数。
对于另外20%的数据,保证n为2的正整数次幂。
对于80%的数据,n≤1024。
对于100%的数据,1≤n≤1×107。
只需要判断二进制就行,如果把他的二进制弄出来,输出就行,
#include<iostream> #include<algorithm> #include<cstring> using namespace std; const int maxn=6e5+100; int a[maxn]; int n; int qpow(int a,int b){ int ans=1; while(b){ if(b&1){ ans=ans*a; } a=a*a; b/=2; } return ans; } int main(){ cin>>n; int cnt=0; while(n){ if(n%2){ a[++cnt]=1; } else{ a[++cnt]=0; } n/=2; } if(a[1]==1){ printf("-1 "); } else{ for(int i=cnt;i>=1;i--){ if(a[i]==1){ cout<<qpow(2,i-1)<<" "; } } } }
问题 F: 直播获奖
NOI2130即将举行。为了增加观赏性,CCF决定逐一评出每个选手的成
绩,并直播即时的获奖分数线。本次竞赛的获奖率为w%,即当前排名前w%的选手的最低成绩就是即时的分数线。
更具体地,若当前已评出了p个选手的成绩,则当前计划获奖人数为max(1,⌊p×w%⌋),其中w是获奖百分比,⌊x⌋表示对x向下取整,max(x,y)表示x和y中较大的数。如有选手成绩相同,则所有成绩并列的选手都能获奖,因此实际获奖人数可能比计划中多。
作为评测组的技术人员,请你帮CCF写一个直播程序。
绩,并直播即时的获奖分数线。本次竞赛的获奖率为w%,即当前排名前w%的选手的最低成绩就是即时的分数线。
更具体地,若当前已评出了p个选手的成绩,则当前计划获奖人数为max(1,⌊p×w%⌋),其中w是获奖百分比,⌊x⌋表示对x向下取整,max(x,y)表示x和y中较大的数。如有选手成绩相同,则所有成绩并列的选手都能获奖,因此实际获奖人数可能比计划中多。
作为评测组的技术人员,请你帮CCF写一个直播程序。
输入
第1行两个正整数n,w。分别代表选手总数与获奖率。
第2行有n个非负整数,依次代表逐一评出的选手成绩。
第2行有n个非负整数,依次代表逐一评出的选手成绩。
输出
只有一行,包含n个非负整数,依次代表选手成绩逐一评出后,即时的获奖分数线。相邻两个整数间用一个空格分隔。
样例输入 Copy
【样例1】
10 60
200 300 400 500 600 600 0 300 200 100
【样例2】
10 30
100 100 600 100 100 100 100 100 100 100
样例输出 Copy
【样例1】 200 300 400 400 400 500 400 400 300 300 【样例2】 100 100 600 600 600 600 100 100 100 100
提示


注意,在第9名选手的成绩评出之后,计划获奖人数为5人,但由于有并列,因此实际会有6人获奖。


对于所有测试点,每个选手的成绩均为不超过600的非负整数,获奖百分比w是一个正整数且1≤w≤99。
在计算计划获奖人数时,如用浮点类型的变量(如C/C++中的float、double,Pascal中的real、double、extended等)存储获奖比例w%,则计算5×60%时的结果可能为3.000001,也可能为2.999999,向下取整后的结果不确定。因此,建议仅使用整型变量,以计算出准确值。
问题 H: 方格取数
设有n×m的方格图,每个方格中都有一个整数。现有一只小熊,想从图的左上角走到右下角,每一步只能向上、向下或向右走一格,并且不能重复经过已经走过的方格,也不能走出边界。小熊会取走所有经过的方格中的整数,求它能取到的整数之和的最大值。
输入
第1行两个正整数n,m。
接下来n行每行m个整数,依次代表每个方格中的整数。
接下来n行每行m个整数,依次代表每个方格中的整数。
输出
一个整数,表示小熊能取到的整数之和的最大值。
样例输入 Copy
【样例1】
3 4
1 -1 3 2
2 -1 4 -1
-2 2 -3 -1
【样例2】
2 5
-1 -1 -3 -2 -7
-2 -1 -4 -1 -2
样例输出 Copy
【样例1】 9 【样例2】 -10
着个取数和其他的不一样,就是这个可以向上取
只需要设置三个数组就可以了
注意要先转移列,就是转移down数组的时候先转倒着转移
#include<iostream> #include<algorithm> using namespace std; const int maxn=1e3+100; const int INF=0x3f3f3f3f; typedef long long ll; ll up[maxn][maxn]; ll down[maxn][maxn]; ll le[maxn][maxn]; ll a[maxn][maxn]; int main(){ int n,m; cin>>n>>m; for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ cin>>a[i][j]; le[i][j]=-0x3f3f3f3f; down[i][j]=-0x3f3f3f3f; up[i][j]=-0x3f3f3f3f; } } le[1][1]=down[1][1]=up[1][1]=a[1][1]; for(int j=1;j<=m;j++){ for(int i=1;i<=n;i++){ if(i!=1){ up[i][j]=max(le[i-1][j],up[i-1][j])+a[i][j]; } if(j!=1){ le[i][j]=max(le[i][j-1],max(up[i][j-1],down[i][j-1]))+a[i][j]; } } for(int i=n-1;i>=1;i--){ down[i][j]=max(le[i+1][j],down[i+1][j])+a[i][j]; } } printf("%lld ",max(le[n][m],up[n][m])); }
问题 I: 约会序列
众所周知,HYF有很多小姊妹。
HYF的小姊妹军团共有N个人,他每天选择一个不同的MM约会。现在HYF想把未来的N天里要约会的MM做一个计划……
首先,他按照自己的标准把N个MM分成A等~Z等,当然A等是质量最好的,Z等是质量最差的(可怜的Z等MM……),然后把她们随机地排成一个队列,比如ACDBCB。HYF决定每次选择队列最前或最后的MM约会,约过的MM就从队列中删去,这样就得到一个长度为N的约会序列。不同的选择方式会得到不同的约会序列,贪心的HYF当然希望先约质量高的MM啦!所以他希望得到所有约会序列中字典序最小的那个。
请你写一个程序帮他确定这样的约会序列。
HYF的小姊妹军团共有N个人,他每天选择一个不同的MM约会。现在HYF想把未来的N天里要约会的MM做一个计划……
首先,他按照自己的标准把N个MM分成A等~Z等,当然A等是质量最好的,Z等是质量最差的(可怜的Z等MM……),然后把她们随机地排成一个队列,比如ACDBCB。HYF决定每次选择队列最前或最后的MM约会,约过的MM就从队列中删去,这样就得到一个长度为N的约会序列。不同的选择方式会得到不同的约会序列,贪心的HYF当然希望先约质量高的MM啦!所以他希望得到所有约会序列中字典序最小的那个。
请你写一个程序帮他确定这样的约会序列。
输入
第一行一个正整数N,表示一共N个MM
接下来N行,每行一个大写字母,表示队列中第i个MM的级别
接下来N行,每行一个大写字母,表示队列中第i个MM的级别
输出
一行一个长度为N的字符串,表示约会序列中字典序最小的那个。
样例输入 Copy
6
A
C
D
B
C
B
样例输出 Copy
ABCBCD
提示
30%的数据,N<=20
60%的数据,N<=100
100%的数据,N<=2000
60%的数据,N<=100
100%的数据,N<=2000
题意就是说,给你一个序列,你可以从两边取数,就是两边取最小的那个就行,如果说一样大,就在向里枚举一个
#include<iostream> #include<algorithm> using namespace std; const int maxn=1e6+100; char a[maxn]; int n; char b[maxn]; int main(){ cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; } int l=1,r=n; int cnt=0; while(r>=l){ if(a[l]<a[r]){ b[++cnt]=a[l]; l++; } else if(a[l]>a[r]){ b[++cnt]=a[r]; r--; } else{ int flag=0; int ll=l+1,rr=r-1; while(rr>=ll){ if(a[ll]<a[rr]){ flag=1; break; } if(a[ll]>a[rr]){ flag=0; break; } ll++; rr--; } if(flag==0){ b[++cnt]=a[r]; r--; } else{ b[++cnt]=a[l]; l++; } } } for(int i=1;i<=n;i++){ cout<<b[i]; } }
问题 J: 直角三角形
在平面直角坐标系上有N个点。
编写程序,统计出这N个点能构成多少个两直角边分别平行于坐标轴的直角三角形。
编写程序,统计出这N个点能构成多少个两直角边分别平行于坐标轴的直角三角形。
输入
输入共有两行:
第1行:输入一个整数N,(3≤N≤500,000);
第2行到N+1行:每行两个正整数X,Y(1≤X,Y≤500,000),代表点的坐标。
第1行:输入一个整数N,(3≤N≤500,000);
第2行到N+1行:每行两个正整数X,Y(1≤X,Y≤500,000),代表点的坐标。
输出
输出只有一行,
输出直角三角形的个数。
输出直角三角形的个数。
样例输入 Copy
【样例1】
3
4 2
2 1
1 2
【样例2】
6
10 10
20 10
10 20
20 20
30 20
30 30
样例输出 Copy
【样例1】
0
【样例2】
8
提示
对于全部40%的数据,保证N≤100;
对于全部70%的数据,保证N≤10,000;
对于全部的数据,保证N≤500,000;


对于全部70%的数据,保证N≤10,000;
对于全部的数据,保证N≤500,000;
这个题很简单,哎当时没想起来,还是大佬告诉我的
就是把每一个横纵坐标记录一下,
在枚举一下每一个点,权值就是(xx[a[i].x]-1)*(yy[a[i].y-1)
至于为什么是这样,自己画图看看
#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1e6+100; struct node{ int x,y; }a[maxn]; int xx[maxn]; int yy[maxn]; int main(){ int n; cin>>n; for(int i=1;i<=n;i++){ cin>>a[i].x>>a[i].y; xx[a[i].x]++; yy[a[i].y]++; } ll ans=0; for(int i=1;i<=n;i++){ ans+=1ll*(xx[a[i].x]-1)*(yy[a[i].y]-1); } cout<<ans<<endl; }
问题 B: 打包
某个工厂生产出的产品都要被打包放入正四棱柱的盒子内。所有盒子的高度都为h,但底面的尺寸不同,可以为11,22,33,44,55,或66,如图所示。
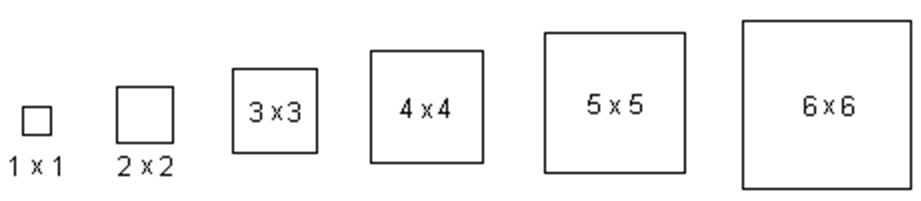
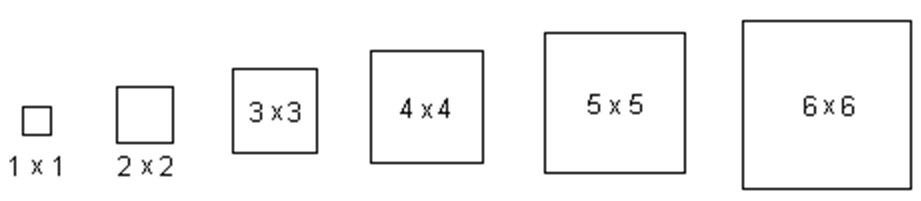 这些盒子将被放入高度为h,底面尺寸为66的箱子里,送到消费者手中。为了降低运送成本,工厂希望尽量减少箱子的数量。如果有一个好的算法,能使箱子的数量降到最低,这将给工厂节省不少资金。请你写一个这样的程序。
这些盒子将被放入高度为h,底面尺寸为66的箱子里,送到消费者手中。为了降低运送成本,工厂希望尽量减少箱子的数量。如果有一个好的算法,能使箱子的数量降到最低,这将给工厂节省不少资金。请你写一个这样的程序。

 这些盒子将被放入高度为h,底面尺寸为66的箱子里,送到消费者手中。为了降低运送成本,工厂希望尽量减少箱子的数量。如果有一个好的算法,能使箱子的数量降到最低,这将给工厂节省不少资金。请你写一个这样的程序。
这些盒子将被放入高度为h,底面尺寸为66的箱子里,送到消费者手中。为了降低运送成本,工厂希望尽量减少箱子的数量。如果有一个好的算法,能使箱子的数量降到最低,这将给工厂节省不少资金。请你写一个这样的程序。输入
六个非负整数a1, a2, a3, a4, a5, a6。它们分别为底面尺寸为11,22,33,44,55,66的盒子的个数。每两个数之间有一个空格。
输出
一个数B,即箱子的最少个数。
例如a1, a2, a3, a4, a5, a6分别为0, 0, 4, 0, 0, 1时,B=2;又例如a1, a2, a3, a4, a5, a6分别为7, 5, 1, 0, 0, 0时,B=1。如图所示。
例如a1, a2, a3, a4, a5, a6分别为0, 0, 4, 0, 0, 1时,B=2;又例如a1, a2, a3, a4, a5, a6分别为7, 5, 1, 0, 0, 0时,B=1。如图所示。


样例输入 Copy
0 0 4 0 0 1
样例输出 Copy
2
这个题当时没有数据
就是贪心的思路

不知道代码对不对
#include<iostream> #include<algorithm> using namespace std; int a[10]; int main(){ for(int i=1;i<=6;i++){ cin>>a[i]; } int ans=a[6]; if(a[5]!=0){//放5 int t=a[1]; if(a[1]!=0){ while(1){ a[5]--; a[1]-=11; ans++; if(a[5]==0||a[1]<=0){ break; } } if(a[1]<0){ a[1]=0; } if(a[5]>0){ ans+=a[5]; } } else{ ans+=a[5]; } } if(a[4]!=0){//放4 if(a[2]!=0){ int p=a[2]/5; int z=a[2]%5; if(p==a[4]){//正好 ans+=a[4]; a[2]=z; } else if(p<a[4]){//a[2]多 a[2]-=a[4]*5; ans+=a[4]; } else{//a[4]多 ans+=p; a[4]-=p; //装1 while(a[4]){ a[4]--; a[1]-=20; ans++; if(a[4]<0||a[1]<0){ break; } } if(a[1]<0){ a[1]=0; } if(a[4]>0){ ans+=a[4]; } } } else{ while(1){ ans++; a[1]-=20; a[4]--; if(a[4]<0||a[1]<0){ break; } } if(a[1]<0){ a[1]=0; } if(a[4]>0){ ans+=a[4]; } } } if(a[3]!=0){//放3 int flag=a[3]%4; if(flag==0) ans+=a[3]/4; else { ans+=a[3]/4+1; if(flag==1) { if(a[2]>5) a[2]-=5; else a[2]=0; if(a[1]>7) a[1]-=7; else a[1]=0; } if(flag==2) { if(a[2]>3) a[2]-=3; else a[2]=0; if(a[1]>6) a[1]-=6; else a[1]=0; } if(flag==3) { if(a[2]>1) a[2]-=1; else a[2]=0; if(a[1]>5) a[1]-=5; else a[1]=0; } } a[3]=0; } if(a[2]!=0){ int flag=a[2]%9; if(flag==0) ans+=a[2]/9; else { ans+=a[2]/9+1; if(a[1]>(36-(flag*4))) a[1]-=(36-(flag*4)); else a[1]=0; } a[2]=0; } if(a[1]){ int flag=a[1]%36; if(flag==0) ans+=a[1]/36; else ans+=a[1]/36+1; a[1]=0; } cout<<ans<<endl; }
代码2

#pragma GCC optimize(2) #include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=1e6+7; const int mod=1e9+7; ll m,n,i,j; ll ans; ll a[10]; int main() { for(ll i=1;i<=6;i++) cin>>a[i]; for(ll i=6;i>=1;i--) { if(a[i]==0) continue; if(i==6) { ans+=a[i]; a[i]=0; } if(i==5) { ans+=a[i]; for(ll j=a[i];j>=1;j--) { if(a[1]>11) a[1]-=11; else { a[1]=0; break; } } a[i]=0; } if(i==4) { ll cnt=0; ans+=a[i]; for(ll j=a[i];j>=1;j--) { if(a[2]>5) a[2]-=5; else { cnt=((5-a[2])+5*(a[i]-j-1))*4; a[2]=0; break; } } if(a[1]>cnt) a[1]-=cnt; else a[1]=0; a[i]=0; } if(i==3) { ll flag=a[i]%4; if(flag==0) ans+=a[i]/4; else { ans+=a[i]/4+1; if(flag==1) { if(a[2]>5) a[2]-=5; else a[2]=0; if(a[1]>7) a[1]-=7; else a[1]=0; } if(flag==2) { if(a[2]>3) a[2]-=3; else a[2]=0; if(a[1]>6) a[1]-=6; else a[1]=0; } if(flag==3) { if(a[2]>1) a[2]-=1; else a[2]=0; if(a[1]>5) a[1]-=5; else a[1]=0; } } a[i]=0; } if(i==2) { ll flag=a[i]%9; if(flag==0) ans+=a[i]/9; else { ans+=a[i]/9+1; if(a[1]>(36-(flag*4))) a[1]-=(36-(flag*4)); else a[1]=0; } a[i]=0; } if(i==1) { ll flag=a[i]%36; if(flag==0) ans+=a[i]/36; else ans+=a[i]/36+1; a[i]=0; } //cout<<a[1]<<" "<<a[2]<<endl; } cout<<ans<<endl; return 0; }
问题 E: 巨石阵
大嘴猴在森林里发现了一个神奇的排成一排的巨石阵。每晚在每块巨石上都会出现若干根好吃的香蕉,当太阳升起时,所有香蕉就会消失。大嘴猴发现一个规律,如果它拿走相邻两块巨石上的香蕉,那么巨石阵很久都不会出产香蕉。大嘴猴想知道,在每晚都能吃到香蕉的情况下,一晚能拿走的最多的香蕉数量。
输入
输入共两行
第一行1个正整数n,表示巨石的数量第二行n个非负整数,以空格分隔,表示每块巨石上的香蕉数量stone[i]
第一行1个正整数n,表示巨石的数量第二行n个非负整数,以空格分隔,表示每块巨石上的香蕉数量stone[i]
输出
输出共一行
第一行1个整数,表示大嘴猴一晚最多能拿走的香蕉数量
第一行1个整数,表示大嘴猴一晚最多能拿走的香蕉数量
样例输入 Copy
【样例1】
4
5 3 7 2
【样例2】
6
3 9 7 2 5 1
样例输出 Copy
【样例1】
12
【样例2】
15
提示
样例1解释:拿走1号巨石上的香蕉 (香蕉数量 = 5) ,然后拿走3号巨石上的香蕉 (香蕉数量 = 7)。一晚能拿走香蕉的最高数量 = 5 + 7 = 12 。
样例2解释:拿走1号巨石上的香蕉(香蕉数量 = 3), 然后拿走3号巨石上的香蕉 (香蕉数量 = 7),然后拿走5号巨石上的香蕉 (香蕉数量 = 5)。一晚能拿走香蕉的最高数量 = 3 + 7 + 5 = 15 。
数据范围与约定0<n≤100,0≤stone[i]≤400
样例2解释:拿走1号巨石上的香蕉(香蕉数量 = 3), 然后拿走3号巨石上的香蕉 (香蕉数量 = 7),然后拿走5号巨石上的香蕉 (香蕉数量 = 5)。一晚能拿走香蕉的最高数量 = 3 + 7 + 5 = 15 。
数据范围与约定0<n≤100,0≤stone[i]≤400
刚好前天做了一个查不多的dp
就是dp[i][0]指的时前i个并且第i个不取的最大值
所以说dp[i][0]=max(dp[i-1][1],dp[i-1][0])
就是dp[i][1]指的时前i个并且第i个取的最大值
所以说dp[i][1]=dp[i-1][0]+a[i]
最后输出max(dp[n][1],dp[n][0])
#include<iostream> #include<algorithm> using namespace std; const int maxn=1e3+100; int dp[maxn][2]; int a[maxn]; int main(){ int n; cin>>n; for(int i=1;i<=n;i++){ cin>>a[i]; } for(int i=1;i<=n;i++){ dp[i][1]=dp[i-1][0]+a[i]; dp[i][0]=max(dp[i-1][0],dp[i-1][1]); } cout<<max(dp[n][0],dp[n][1])<<endl; }
问题 F: 二师兄的纪录片
二师兄护送师傅取经成功之后,成了名人,他决定重新把取经的路再走一遍,并且拍摄一部纪录片宣传路上的风光。
从东土大唐到天竺的地图,是正方形的,城市坐落在 N 行 N 列的方形地图上。地图从位置(1,1)排列到位置(N,N)。地图上每一个格子是一座城市,上下左右直接相邻的城市之间可以一天到达。
有 P 座城市住着野蛮人(野蛮城市),他们只吃红烧肉。一天三顿红烧肉,连早餐都吃红烧肉。二师兄是出家人,决定不去这些城市。
另有 Q 座城市(友好城市)希望二师兄帮他们多宣传城市风光,所以给二师兄提供一个优惠条件:如果二师兄在这座城市(X)停留三天,就可以在第四天派专机把二师兄送到另外一座城市 Y。从城市 X 飞到城市 Y 可以瞬间完成,即:二师兄在到达X城市后,可以选择四天后到达Y城市。当然,二师兄也可以选择只在X城市停留一天,然后访问X城市直接相邻的城市。
已知长安城位于地图的(1,1)位置,目的地灵山位于地图的 (N,N)位置。每一个友好城市只能直飞到另外一个城市。
请求出二师兄从长安到达灵山最少需要多少天。
从东土大唐到天竺的地图,是正方形的,城市坐落在 N 行 N 列的方形地图上。地图从位置(1,1)排列到位置(N,N)。地图上每一个格子是一座城市,上下左右直接相邻的城市之间可以一天到达。
有 P 座城市住着野蛮人(野蛮城市),他们只吃红烧肉。一天三顿红烧肉,连早餐都吃红烧肉。二师兄是出家人,决定不去这些城市。
另有 Q 座城市(友好城市)希望二师兄帮他们多宣传城市风光,所以给二师兄提供一个优惠条件:如果二师兄在这座城市(X)停留三天,就可以在第四天派专机把二师兄送到另外一座城市 Y。从城市 X 飞到城市 Y 可以瞬间完成,即:二师兄在到达X城市后,可以选择四天后到达Y城市。当然,二师兄也可以选择只在X城市停留一天,然后访问X城市直接相邻的城市。
已知长安城位于地图的(1,1)位置,目的地灵山位于地图的 (N,N)位置。每一个友好城市只能直飞到另外一个城市。
请求出二师兄从长安到达灵山最少需要多少天。
输入
输入数据第一行有三个整数,分别是 N,P,Q。
整数之间用空格分开。城市坐标系X轴向下,起点为1,Y 轴向右,起点为1。
数据接下来的 P 行,每行两个整数 a,b,代表某一个野蛮城市的坐标 (a,b)。
位置信息 (a,b) 表示在 X-Y 坐标系中的位置。
再接下来的 Q 行,每行四个整数,代表友好城市 X 的坐标和从X能直飞的城市 Y 的坐标。
整数之间用空格分开。城市坐标系X轴向下,起点为1,Y 轴向右,起点为1。
数据接下来的 P 行,每行两个整数 a,b,代表某一个野蛮城市的坐标 (a,b)。
位置信息 (a,b) 表示在 X-Y 坐标系中的位置。
再接下来的 Q 行,每行四个整数,代表友好城市 X 的坐标和从X能直飞的城市 Y 的坐标。
输出
输出数据一行,表示二师兄从长安去往灵山最少需要多少天。
如果从长安到达不了灵山,则输出-1。
二师兄在长安出发那天记为第1天,到达灵山那天的日期就是输出数据。
如果从长安到达不了灵山,则输出-1。
二师兄在长安出发那天记为第1天,到达灵山那天的日期就是输出数据。
样例输入 Copy
【样例1】
5 7 0
1 2
2 4
3 2
3 4
4 2
4 4
5 4
【样例2】
9 27 1
1 2
1 6
2 4
2 6
2 8
3 2
3 4
3 6
3 8
4 2
4 4
4 6
4 8
5 4
5 6
5 8
6 4
6 6
6 8
7 4
7 6
7 8
8 4
8 6
8 8
9 4
9 8
6 2 8 9
样例输出 Copy
【样例1】
11
【样例2】
12
提示
样例1解释样例数据后面的解释说明当中,“.”代表可以访问的普通城市,“#”代表野蛮城市。“1”代表X城市和能从“1”直飞的城市Y。
原地图:
原地图:

样例1原地图.png


到达目的地的走法:


样例2解释样例数据后面的解释说明当中,“.”代表可以访问的普通城市,“#”代表野蛮城市。“1”代表X城市和能从“1”直飞的城市Y。
原地图:

走法说明:走到 6 2 点的时候,穿越到 8 9 点。



这个题就是一个带传送门的BFS但是我不会,我用最短路跑到
跑最短路的时候就是说,把每一个点都编上号,在每一个点向四周建图
#include<iostream> #include<algorithm> #include<cstring> using namespace std; const int INF=0x3f3f3f3f; const int maxn=2e3+100; const int maxx=1e6+1000; typedef long long ll; int a[maxn][maxn]; int s[maxn][maxn]; int n,p,q; int L=0; struct node{ int e,next; int w; }edge[maxx]; int cnt=0; int head[maxx],vis[maxx]; int dis[maxx]; void add(int u,int v,int w){ edge[cnt].e=v; edge[cnt].w=w; edge[cnt].next=head[u]; head[u]=cnt++; } void di(int s){ for(int i=0;i<=L;i++) dis[i]=INF,vis[i]=0; dis[s]=0; while(1){ int k=-1; ll minl=INF; for(int i=1;i<=L;i++){ if(!vis[i]&&minl>dis[i]){ k=i; minl=dis[i]; } } if(k==-1) break; vis[k]=1; for(int i=head[k];~i;i=edge[i].next){ int e=edge[i].e; if(dis[e]>dis[k]+edge[i].w){///松弛操作 也叫更新操作 dis[e]=dis[k]+edge[i].w; } } } } int main(){ memset(head,-1,sizeof(head)); cin>>n>>p>>q; for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ a[i][j]=++L; } } int x1,y1,x2,y2; for(int i=1;i<=p;i++){ cin>>x1>>y1; s[x1][y1]=1; } for(int i=1;i<=q;i++){ cin>>x1>>y1>>x2>>y2; add(a[x1][y1],a[x2][y2],4); } for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ if(s[i][j]==1){ continue; } if(i-1>=1&&s[i-1][j]!=1){ add(a[i][j],a[i-1][j],1); add(a[i-1][j],a[i][j],1); } if(j-1>=1&&s[i][j-1]!=1){ add(a[i][j],a[i][j-1],1); add(a[i][j-1],a[i][j],1); } if(s[i+1][j]!=1){ add(a[i][j],a[i+1][j],1); add(a[i+1][j],a[i][j],1); } if(s[i][j+1]!=1){ add(a[i][j],a[i][j+1],1); add(a[i][j+1],a[i][j],1); } } } di(1); if(dis[a[n][n]]!=INF) cout<<dis[a[n][n]]+1<<endl; else{ cout<<-1<<endl; } }
问题 G: 算术 (math)
若是万一琪露诺进行攻击,什么都好,冷静地说些话题来吸引她,对方表现出兴趣的话,那就慢慢地提问。随后,在她考虑答案的时候,趁机逃吧。就算是很简单的问题,她一定也答不上来。——「求闻史记」
那么你就恰好遭受到了琪露诺的攻击,在危机之下,你丢出了这样一个问题:
有A+B个数字,每个数字为1-9中的一个。将这A+B个数字按位次拼接成两个十进制数,一个恰好有A位,另一个恰好有B位,使得这两个数的乘积之和最大。
那么显而易见你成功脱离了危险,之后你开始思考如何解决你提出的问题。
那么你就恰好遭受到了琪露诺的攻击,在危机之下,你丢出了这样一个问题:
有A+B个数字,每个数字为1-9中的一个。将这A+B个数字按位次拼接成两个十进制数,一个恰好有A位,另一个恰好有B位,使得这两个数的乘积之和最大。
那么显而易见你成功脱离了危险,之后你开始思考如何解决你提出的问题。
输入
第一行,一个整数T ,表示有T组询问。
对于每一行询问,第一行:A,B。
接下来一行,9个整数;分别代表1-9的个数,保证个数和为A+B。
对于每一行询问,第一行:A,B。
接下来一行,9个整数;分别代表1-9的个数,保证个数和为A+B。
输出
对于每一组询问,回答一个整数,表示能得到最大的成绩之和
样例输入 Copy
1
2 7
1 1 1 1 1 1 1 1 1
样例输出 Copy
840414816
提示
样例解释:最大值为96×8754321



这个题一看就是大数+贪心
首先你先从9到0遍历数组找到第一个是s[i]为奇数的位数tag,
然后还是倒着从9到0遍历,比较一下num1和num2(填数的数组的大小),如果num1小就加入到aa,如果num2小就加入到bb中,
如果num1==num2的话如果i<tag就添加到bb中,否则就添加到aa中,
因为是如果添加到aa中aa是短的那个,aa*bb才会最大(这个我也不理解)
#include<iostream> #include<algorithm> #include<vector> #include<cstring> using namespace std; const int maxn=1e5+1000; int s[maxn]; string mult(string A,string B){ int x[maxn],y[maxn],z[maxn<<1]; string c; memset(x,0,sizeof(x)); memset(y,0,sizeof(y)); memset(z,0,sizeof(z)); for(int i=A.size()-1,cnt=0;i>=0;i--) x[cnt++]=A[i]-'0'; for(int i=B.size()-1,cnt=0;i>=0;i--) y[cnt++]=B[i]-'0'; for(int i=0;i<A.size();i++) for(int j=0;j<B.size();j++) z[i+j]+=x[i]*y[j]; for(int i=0;i<maxn*2;i++){ if(z[i]>=10){ z[i+1]=z[i+1]+z[i]/10; z[i]=z[i]%10; } } int cot=maxn*2-1; while(z[cot]==0) cot--; while(cot>=0) c.push_back(z[cot--]+'0'); return c; } int main(){ int t; cin>>t; while(t--){ string aa,bb; int a,b; cin>>a>>b; if(a>b){ swap(a,b); } for(int i=1;i<=9;i++){ cin>>s[i]; } int tag=-1; for(int i=9;i>=0;i--){ if(s[i]&1){ tag=i; break; } } int i; int num1=0; int num2=0; int flag=0; for(i=9;i>=1;i--){ if(!s[i]){ continue; } if(!flag&&i<tag){ flag=1; } while(s[i]>0){ s[i]--; if(num1==num2&&!flag){ aa+=(i+'0'); num1++; } else if(num1==num2&&flag){ bb+=(i+'0'); num2++; } else{ if(num1<num2){ aa+=i+'0'; num1++; } else{ bb+=i+'0'; num2++; } } if(num1==a){ break; } } if(num1==a){ break; } } while(i){ if(!s[i]) { i--; continue; } s[i]--; bb+=i+'0'; } cout<<aa<<" "<<bb<<endl; string p=mult(aa,bb); cout<<p<<endl; } }

