剑指：数组中的逆序对

题目描述

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007

输入描述:

题目保证输入的数组中没有的相同的数字

数据范围：

对于%50的数据,size<=10^4

对于%75的数据,size<=10^5

对于%100的数据,size<=2*10^5

示例1

输入

1,2,3,4,5,6,7,0

输出

7

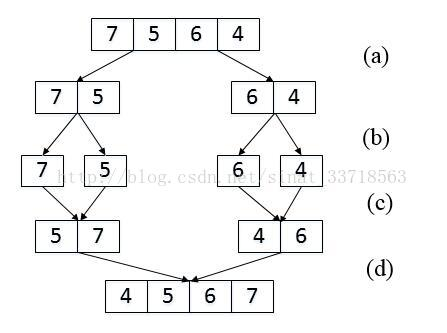
解：

如：

(a) 把长度为4的数组分解成两个长度为2的子数组；

(b) 把长度为2的数组分解成两个成都为1的子数组；

(c) 把长度为1的子数组 合并、排序并统计逆序对 ；

(d) 把长度为2的子数组合并、排序，并统计逆序对；

import java.util.Arrays;

public class Solution {

     public static int InversePairs(int [] array) {
        if(array==null||array.length==0)
        {
            return 0;
        }
        
//        int[] copy = new int[array.length];
//        for(int i=0;i<array.length;i++)
//        {
//            copy[i] = array[i];
//        }
        int[] copy = Arrays.copyOf(array, array.length);
        int count = InversePairsCore(array,copy,0,array.length-1);//数值过大求余
        return count;   
     }

    private static int InversePairsCore(int[] array, int[] copy, int l, int r) {
        if(l==r){
            return 0;
        }
        int mid = l + ((r-l)>>1);
        int lCount = InversePairsCore(array,copy, l, mid)%1000000007;
        int rCount = InversePairsCore(array,copy, mid+1, r)%1000000007;
        int count = 0;
        int i=mid;
        int j=r;
        int locCopy = r;
        while(i>=l && j>mid){
            if(array[i]>array[j]){
                count += j-mid; //此注意边界
                copy[locCopy--] = array[i--];
                if(count>=1000000007)//数值过大求余
                {
                    count%=1000000007;
                }
            }else{
                copy[locCopy--] = array[j--];
            }
        }
        
        while(i>=l){
            copy[locCopy--] = array[i--];
        }
        while(j>mid){
            copy[locCopy--] = array[j--];
        }
        
        for(int s=l; s<=r; s++){
            array[s] = copy[s];
        }
        
        return (lCount+rCount+count)%1000000007;
    }


    public static void main(String[] args) {
        int[] arr = {1,5,0,3,2};
        int res = InversePairs(arr);
        System.out.println(res);
    }
}