补码乘法 & 波兹乘法器

1. 补码数

正数表示：

$ N = sum_{i=0}^{i=n-1}2^{i} $

负数表示

$ N = -[1+sum_{i=0}^{n-1}(1-a_i)2^i] $

经过推到合并，将an符号项加入，可以写为：

$ N = -a_n2^n+sum_{i=0}^{n-1}a_i2^i $

因而，两数相乘，可以用如下式子表示：

$ P = ( -y_n2^n+sum_{i=0}^{n-1}y_i2^i)( -a_x2^n+sum_{i=0}^{n-1}x_i2^i)) $ 

2. 减少部分积的数目

首先我们讨论通常情况下的乘法器原理。

如下示例：

　　　　　 0 0 1 0 1 1  y
                0 1 0 0 1 1  x
                0 0 1 0 1 1
              0 0 1 0 1 1
            0 0 0 0 0 0
          0 0 0 0 0 0
        0 0 1 0 1 1     
        0 0 1 1 0 1 0 0 0 1

在该系统中，通过移位并相加的方法得到最终的结果。中间的每个横行就是部分积。部分积的个数与x的位数相同。

此运算为模2的运算。如果采用高基运算，即可减少部分积的数目。

模4的运算，对于Y而言，可以分为0Y, 1Y, 2Y, 3Y，但是3Y为高阶项，比较难以实现，于是考虑只用0Y, 1Y, 2Y实现模4运算。

由此出现了波兹编码。

3. 波兹编码

编码的方式是每个block里面3个数，并且会有overlaps，如下所示：

编码表如下：

Block	Partial Product
000	0
001	1 * Multiplicand
010	1 * Multiplicand
011	2 * Multiplicand
100	-2 * Multiplicand
101	-1 * Multiplicand
110	-1 * Multiplicand
111	0

 这里有个疑问，为什么001，010的partial product是一样的呢？

对LSB和MSB的处理：

LSB可以往后补0，MSB可以往前补0。

4. 波兹编码乘法器的计算示例：

（1）

　　　　　 0 0 1 0 1 1  , multiplicand
                0 1 0 0 1 1  , multiplier
                   1   1  -1  , booth encoding of multiplier
	1 1 1 1 1 1 0 1 0 0  , negative term sign extended
            0 0 1 0 1 1
        0 0 1 0 1 1
                  0 0 0 0 1  , error correction for negation
        0 0 1 1 0 1 0 0 0 1  , discarding the carried high bit

 

（2） 

　　　　　 0 1 1 0 0 1  , multiplicand
                1 0 0 1 1 1  , multiplier
              1  -2   2  -1  , booth encoding of multiplier
	1 1 1 1 1 0 0 1 1 0  , negative term sign extended
    0 0 0 0 1 1 0 0 1 0
    1 1 0 0 1 1 0 1
    0 1 1 0 0 1
          0 0 0 0 1          , error correction for negation
                  0 0 0 0 1  , error correction for negation
    0 0 1 1 1 1 0 0 1 1 1 1  , discarding the carried high bit

 注意这里乘数的最高位是1，因此需要前面补0。并且有两个负值，因此需要进行相应位数的两次error correction。

5. 波兹编码的实现

有一种实现方式如图所示。

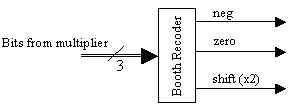
neg为符号位，zero为系数1，shift为系数2。

 

参考：

http://www.geoffknagge.com/fyp/booth.shtml