毕设需要,在蛮早之前就写了这题,没时间记录一下,在这里学到的。
这个是大家耳熟能详的一个方法,用射线法去判断点是否在一个简单多边形内(边不自交,不论凹凸),如果是凸的话,可以有有向面积法,对于凹的还有累积度数法、编码法什么的,具体见计算机图形或是算法相关书籍,不赘述了。
后面加了个数论题,关乎于一个结论,在这里学到的,问说有多少个正整数不能表示成px+py的形式(x>=0,y>=0,p,q是素数且p!=q)。
1 点在多边形内的判断(射线法)
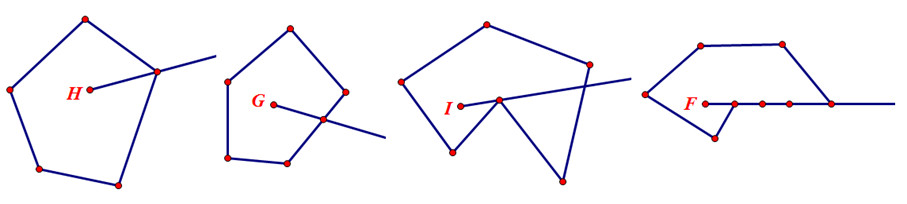
对于相交,考虑下面几个图:
射线经过多边形的情况就这四种,第一种与点相交,第二种与边相交,与点相交可能还在内部,与边相交可能和边重合。对于第1、3、4个,可以用一种巧妙的技巧来处理下,可以使得判断变得简单,就是枚举边的时候,如果边的起始点在射线上的话,就不考虑该边,因此对于有公共顶点的两条边,就不会重复计算两次了,对于有点在射线上的话,如果两边的点在射线异端的话,就统计该店,否则不统计,累计后,判断统计的次数是奇数次,就说明是在多边形内部,否则就不在。对于第四中情况,上边的处理,等同于把中间的那些边都砍掉,退化成第一种的情况了。所以,说白了,就第一种和第二种两种情况,大致算法如下:
1. 枚举边
1.1. if 如果射线和线段直接相交,统计
1.2. elseif 如果射线和有向线段的起始点相交,就continue
1.3. elseif 如果射线和有向线段的终点相交的话,判断两端的点,如果在异侧,就统计
2. 判断统计数的奇偶
题目在这里,代码如下:
/*
判断点是否在多边形内
*/
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <set>
#include <stdio.h>
#include <math.h>
using namespace std;
const int MAX = 100;
const double INF = 1e9;
const double EPS = 1e-6;
//是点也是向量
class CPoint
{
public:
double x, y;
public:
CPoint() {}
CPoint(double _x, double _y)
: x(_x), y(_y) {}
CPoint operator - (CPoint& t) { return CPoint(t.x - x, t.y - y); }
CPoint operator + (CPoint& t) { return CPoint(t.x + x, t.y + y); }
double ChaJi(CPoint t) { return x * t.y - t.x * y; }
double NeiJi(CPoint t) { return x * t.x + y * t.y; }
};
class CLine
{
public:
CPoint x, y;
public:
CLine() {}
CLine(CPoint _x, CPoint _y)
: x(_x), y(_y) {}
double GetMinX() { return min(x.x, y.x); }
double GetMaxX() { return max(x.x, y.x); }
double GetMinY() { return min(x.y, y.y); }
double GetMaxY() { return max(x.y, y.y); }
};
class CPolygon
{
public:
CPoint point[MAX];
CLine line[MAX];
int line_num;
public:
void SetLineByPoint()
{
for(int i = 0; i < line_num; i++)
{
line[i] = CLine(point[i], point[(i + 1) % line_num]);
}
}
bool JudgePointIn(CPoint x)
{
int cnt = 0;
CLine dq = CLine(x, CPoint(INF, x.y));
for(int i = 0; i < line_num; i++)
{
if(PointOnLine(x, line[i])) return true;
if(LineXiangJiao(line[i], dq)) cnt++;
else
{
if(PointOnLine(line[i].x, dq)) continue;
else if(PointOnLine(line[i].y, dq)
&& !OnTheSameSide(line[i].x, line[(i + 1) % line_num].y, dq)) cnt++;
//else if(PointOnLine(line[i].y, dq)
// && PointOnLine(line[(i + 1) % line_num].y, dq)
// && !OnTheSameSide(line[i].x, line[(i + 2) % line_num].y, dq)) cnt++;
}
}
if(cnt & 1) return true;
else return false;
}
//精度控制
bool IsZero(double x) { return fabs(x) < EPS ? true : false; }
bool BigThanZero(double x) { return x >= EPS ? true : false; }
bool SmaThanZero(double x) { return x <= -EPS ? true : false; }
//判断点是否在线段上
bool PointOnLine(CPoint x, CLine L)
{
CPoint da = L.x - x;
CPoint db = L.y - x;
if(IsZero(da.ChaJi(db)) && SmaThanZero(da.NeiJi(db))) return true;
else return false;
}
//两条线段相交,不包括端点
bool LineXiangJiao(CLine x, CLine y)
{
//包围盒测试
if(x.GetMaxX() < y.GetMinX() ||
x.GetMaxY() < y.GetMinY() ||
x.GetMinX() > y.GetMaxX() ||
x.GetMinY() > y.GetMinY()) return false;
if(!OnTheSameSide(x.x, x.y, y) &&
!OnTheSameSide(y.x, y.y, x)) return true;
else return false;
}
//判断x,y是否在L的同侧
bool OnTheSameSide(CPoint x, CPoint y, CLine L)
{
CPoint da, db, dc;
da = L.y - L.x;
db = x - L.x;
dc = y - L.x;
if(SmaThanZero(da.ChaJi(db) * da.ChaJi(dc))) return false;
else return true;
}
};
int main()
{
int n, c = 0;
while(scanf("%d", &n), n)
{
CPolygon m_Polygon;
m_Polygon.line_num = n;
for(int i = 0; i < n; i++)
{
double x, y;
scanf("%lf%lf", &x, &y);
m_Polygon.point[i] = CPoint(x, y);
}
m_Polygon.SetLineByPoint();
//CPoint o;
//scanf("%lf%lf", &o.x, &o.y);
int p, q;
scanf("%d%d", &p, &q);
printf("Pilot %d\n", ++c);
if(m_Polygon.JudgePointIn(CPoint(0, 0)))
printf("The pilot is in danger!\nThe secret number is %d.\n", (p - 1) * (q - 1) / 2);
else printf("The pilot is safe.\n");
printf("\n");
}
}
2 有多少个正整数不能表示为px+py的形式
趁这次机会,把以前学习的一些数论知识重新看了下,觉得比之前深入理解了些。
2.1 最大公约数
求最大公约数GCD(a, b),现在都能背着写出来了,但让我去推导,因为没有了解到本质,所以也不会对复杂度分析,就是常说的“只知其然,不知其所以然”,了解到算法的本质,才可以做到较好的灵活应用,为己所用,现在能记得以前学的东西里面,很大很大的一部分都是来自于推导也说明了这点。
GCD(a, b) = GCD(b, a % b) ,这里假设a > b,因为如果a < b的话,一次GCD之后,就变成了a > b,然后就一直这样下去。把该等式证明后,相信代码就好写了,就是把这两个偏序的数,一致的不断的变小(引自Crazyb0y的话),把规模缩小到可解,然后回朔就是。
我证明这个的方法比较笨,显得臃肿,就是分别证明GCD(a, b) | GCD(b, a % b)和GCD(b, a % b) | GCD(a, b)。这个过程就不详述了,说明其中一个证明过程,记g = GCD(a, b), a > b,然后证g | a % b,因为a = b * x + r, 0 <= r < b,r就是a % b,因为g | a, g | b,所以a = g * d1, b = g * d2,d1, d2 >= 1,a % b = r = a – b * x = g * d1 – g * d2 * x = g * (d1 – d2 * x),所以g | r = (a % b)。
这个求最大公约数的算法就叫做辗转相除法(Euclidean Algorithm),然后这里简单分析它的复杂度(来自Crazyb0y的集训队论文),考虑(a, b) –> (b, a % b)这样一个步骤,它把a变成了a % b,然后下次用同样的手法处理了b,如果b <= a / 2,则a % b < a / 2,如果b > a / 2,则a % b <= a – b < a / 2,所以它把一个数给砍半了,所以复杂度就为log(max(a, b)),就是logN级别的了。
2.2 ax+by=g
将辗转相除法扩展一下就是扩展欧几里得算法(Extended Euclidean Algorithm),下面说明下,如何求出该类方程的一组解。
ax + by = g, g = gcd(a, b),对该方程做下变形,目标是把系数做成辗转相除法中的方法,让它变小,到可解的时候,解出解后回朔,下面用到的除法是正除以。
(a / b * b + a % b)x + by = g => b(a / b * x + y) + (a % b)x + = g
设x’ = a / b * x + y, y’ = x然后递归求出右边等式bx’ + (a % b)y’ = g的解,根据x’,y’求出x,y即可,当a % b = 0的时候,(x’,y’)=(1,0)便是一组解。
下面贴一下欧几里得算法和扩展欧几里得算法的代码:
#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <set>
#include <stdio.h>
#include <math.h>
using namespace std;
int Euclidean_Algorithm(int a, int b) //辗转相除法
{
if(b == 0) return a;
else return Euclidean_Algorithm(b, a % b); //使得a > b
}
void Extended_Euclidean_Algorithm(int a, int b, int& x, int& y) //ax+by=gcd(a,b)=g
{
if(b == 0)
{
x = 1;
y = 0;
return;
}
int xx, yy;
Extended_Euclidean_Algorithm(b, a % b, xx, yy);
x = yy;
y = xx - a / b * yy;
}
int main()
{
int a, b;
while(scanf("%d%d", &a, &b))
{
int x, y;
Extended_Euclidean_Algorithm(a, b, x, y);
printf("%d %d %d\n", Euclidean_Algorithm(a, b),
x, y);
}
}
下面就是关于这道数论的证明,参考这儿:
证明,如果GCD(p, q) = 1,p>=1,q>=1,则不能表示为px+qy,x>=0,y>=0的非负整数有(p-1)*(q-1)/2个,下面一步一步证明,下面的变量如无特别说明,都是整数,
(1) 不能表示为px+qy,x>=0,y>=0,(p,q)=1,p>=1,q>=1的最大正整数是pq-p-q;
先证明pq-p-q不能表示为所述形式:
假设能表示,则pq-p-q=px+qy,
则p(q-1-x)=q(y+1),
则q | (q-1-x), p | (y+1)
则q | (1+x),因为q(y+1)>0,所以q-1-x>0,所以1<=x+1<=q-1,所以产生矛盾,pq-p-q不能表示为上述形式。
再证明pq-p-q是最大的:
先看这样的一个序列1p,2p,3p,…,(q-1)p,这q个数%p后的值是在{0,1,2,q-1}中,因为如果有两个是相等的,设ip=jp(mod q),0<=i<j<=q-1,则(j-i)p%q=0,则(j-i)%q=0,而0<j-i<=q-1,所以产生矛盾,说明上述是正确的。
同理n-1p,n-2p,n-3p,…,n-(q-1)p,这个序列也是一样,所以设(n-up)%q=0,则n=up+vq,u∈[0,q-1],
n=up+vq>pq-p-q,则vq>pq-p-q-up>=pq-p-q-pq+p,推出v>-1,即v>=0,说明对于n是能表示为上述形式的。
(2) 对于任意一个非负整数n,都可表示为n=px+qy,的形式,其中x∈[0, q – 1],y为整数即可;
这个在(1)中已经给出证明,按照那种方法就可以构造出来,这里可以如此调整出来,
知道n=px+qy=p(x-tq)+q(y+tp),可以通过调整x-tq,把它调整至[0,q-1]这个区间内。
(3) m=pq-p-q,对于n和m-n,n∈[0, m],n和m-n这两个数,有且仅有一个能表示为px+qy的形式,(p,q)=1,p>=1,q>=1,x>=0,y>=0;
对于n和m-n都想表示成那种形式,为使u1,u2,v1,v2属于[0,+∞)为此,
n=pu1+qv1, m-n=pu2+qv2,这里u1,u2∈[0, q-1],因为pu1+qv1<=pq-p-q,所以pu1<=pq-p-q-qv1<=pq-p,所以u1<=q-1,同理u2。
所以pq-p-q=pu1+pu2+qv1+qv2,则p(q-1-u1-u2)=q(v1+v2+1),
所以p | (v1+v2+1), q | (q-1-u1-u2),
所以q | (u1+u2+1),因为1<=u1+u2<=2q-1,所以u1+u2+1=q,所以v1+v2=-1,所以v1,v2不能同时>=0,也不能同时<0。只能一个符合要求,一个不符合要求。
(4) 不能表示为px+qy,x>=0,y>=0,(p,q)=1,p>=1,q>=1的整数有(p-1)*(q-1)/2个。
对于[0, pq-p-q]这个区间的pq-p-q+1个数(偶数),能进行和为pq-p-q的配对,共有(p-1)*(q-1)/2对,这些对里面,有且仅有一个是能表示为,另一个是不能表示的,而对于n>pq-p-q,前面已经证明是可以表示为的,所以不能表示为的,共有(p-1)*(q-1)/2个。