ALS分解

1.交替交替最小二乘应该来说是一种优化策略，用来对矩阵进行近似分解

　　

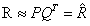
 　　其中，P矩阵维度：N*K；Q矩阵维度：M*K。前者为User在K维潜因子空间的表示；后者为Item在K维潜因子空间的表示。

2.预测评分，或者説近似评分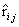为

　　

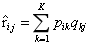
3.损失函数为平方误差+L2正则项，其中是真实值。

　　

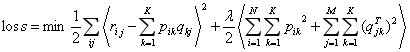
4.交替迭代

• 对P，Q随机初始化

• 固定q，对p求偏导，并令导数为0。其中。

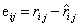　　for k in K:(K为隐因子大小)：

　　　　，即所有用户i评过的项目j（所有项目j上的隐因子k综合起来）

　　最终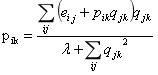，，依次得到所有用户对隐类的偏好。

• 同样，固定p，求q，令导数为0。

 　　

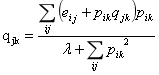
　　迭代执行p和q，固定q⁰，用q⁰求p⁰；固定p⁰，用p⁰求q¹如下迭代下去直到误差小于阈值或达到最大迭代次数。

5.程序，完整程序(数据movielens,100k),https://github.com/jiangnanboy/recommendation_methods/blob/master/com/sy/reco/recommendation/matrix_factorization/als.py

import numpy as np
import math

#这里使用als交替最小二乘求解U,I矩阵
class ALS():
    '''
     初始化ratingMatrix,F, λ
    ratingMatrix:评分矩阵
    F:隐因子数目
    λ:正则化参数，以防过拟合
    '''
    def __init__(self, ratingMatrix, F, λ):
        self.ratingMatrix = ratingMatrix
        self.F = F
        self.λ = λ

    #对U,I矩阵初始化，随机填充，根据经验随机数与1/sqrt(F)成正比
    def __initPQ(self,userSum,itemSum):
        self.U=np.zeros((userSum,self.F))
        self.I=np.zeros((itemSum,self.F))
        for i in range(userSum):
            self.U[i]=[np.random.random()/math.sqrt(self.F) for x in range(self.F)]
        for i in range(itemSum):
            self.I[i]=[np.random.random()/math.sqrt(self.F) for x in range(self.F)]

    #使用交替二乘迭代训练分解，max_iter:迭代次数
    def iteration_train(self,max_iter):
        userSum = len(self.ratingMatrix)  # 用户个数
        itemSum = len(self.ratingMatrix[0])  # 项目个数
        self.__initPQ(userSum,itemSum)#初始化U,I矩阵
        for step in range(max_iter):
            #这时固定self.I，求解self.U
            for user in range(userSum):
                for f in range(self.F):
                    sum_1=0.
                    sum_2=0.
                    for item in range(itemSum):
                        if self.ratingMatrix[user,item]>0:
                            eui=self.ratingMatrix[user,item]-self.predict(user,item)#误差
                            sum_1+=(eui+self.U[user,f]*self.I[item,f])*self.I[item,f]
                            sum_2+=self.I[item,f]**2
                    sum_2+=self.λ
                    self.U[user,f]=sum_1/sum_2
            #这里固定self.U，求解self.I
            for item in range(itemSum):
                for f in range(self.F):
                    sum_1=0.
                    sum_2=0.
                    for user in range(userSum):
                        if self.ratingMatrix[user,item]>0:
                            eui=self.ratingMatrix[user,item]-self.predict(user,item)#误差
                            sum_1+=(eui+self.U[user,f]*self.I[item,f])*self.U[user,f]
                            sum_2+=self.U[user,f]**2
                    sum_2+=self.λ
                    self.I[item,f]=sum_1/sum_2
        return np.round(np.dot(self.U, self.I.T), 0)  # 返回全部，两个矩阵相乘



    #预测打分，用户的行与项目的列
    def predict(self,user,item):
        I_T=self.I.T#项目矩阵转置
        pui=np.dot(self.U[user,:],I_T[:,item])
        return pui