[Python数据挖掘]第5章、挖掘建模（下）

 四、关联规则

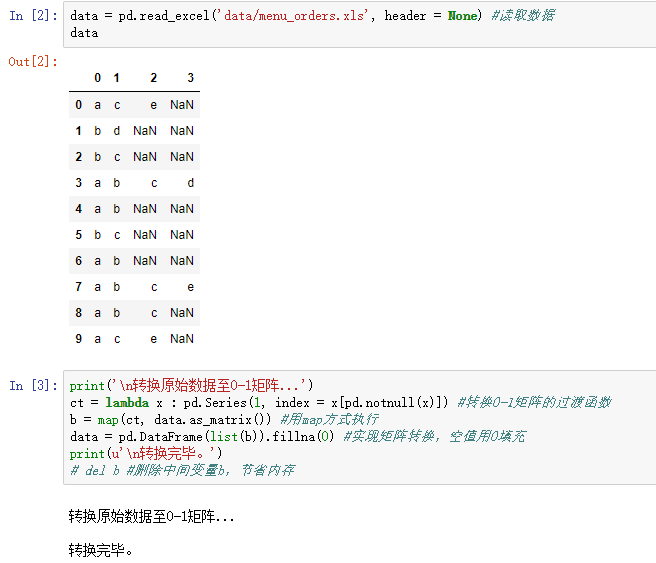
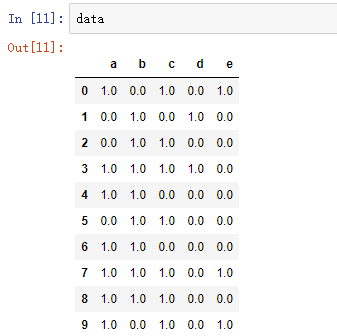
Apriori算法代码（被调函数部分没怎么看懂）

from __future__ import print_function
import pandas as pd

#自定义连接函数，用于实现L_{k-1}到C_k的连接
def connect_string(x, ms):
  x = list(map(lambda i:sorted(i.split(ms)), x))
  l = len(x[0])
  r = []
  for i in range(len(x)):
    for j in range(i,len(x)):
      if x[i][:l-1] == x[j][:l-1] and x[i][l-1] != x[j][l-1]:
        r.append(x[i][:l-1]+sorted([x[j][l-1],x[i][l-1]]))
  return r

#寻找关联规则的函数
def find_rule(d, support, confidence, ms = u'--'):
  result = pd.DataFrame(index=['support', 'confidence']) #定义输出结果
  
  support_series = 1.0*d.sum()/len(d) #支持度序列
  column = list(support_series[support_series > support].index) #初步根据支持度筛选
  k = 0
  
  while len(column) > 1:
    k = k+1
    print(u'
正在进行第%s次搜索...' %k)
    column = connect_string(column, ms)
    print(u'数目：%s...' %len(column))
    sf = lambda i: d[i].prod(axis=1, numeric_only = True) #新一批支持度的计算函数
    
    #创建连接数据，这一步耗时、耗内存最严重。当数据集较大时，可以考虑并行运算优化。
    d_2 = pd.DataFrame(list(map(sf,column)), index = [ms.join(i) for i in column]).T
    
    support_series_2 = 1.0*d_2[[ms.join(i) for i in column]].sum()/len(d) #计算连接后的支持度
    column = list(support_series_2[support_series_2 > support].index) #新一轮支持度筛选
    support_series = support_series.append(support_series_2)
    column2 = []
    
    for i in column: #遍历可能的推理，如{A,B,C}究竟是A+B-->C还是B+C-->A还是C+A-->B？
      i = i.split(ms)
      for j in range(len(i)):
        column2.append(i[:j]+i[j+1:]+i[j:j+1])
    
    cofidence_series = pd.Series(index=[ms.join(i) for i in column2]) #定义置信度序列
 
    for i in column2: #计算置信度序列
      cofidence_series[ms.join(i)] = support_series[ms.join(sorted(i))]/support_series[ms.join(i[:len(i)-1])]
    
    for i in cofidence_series[cofidence_series > confidence].index: #置信度筛选
      result[i] = 0.0
      result[i]['confidence'] = cofidence_series[i]
      result[i]['support'] = support_series[ms.join(sorted(i.split(ms)))]
  
  result = result.T.sort_values(['confidence','support'], ascending = False) #结果整理，输出
  print(u'
结果为：')
  print(result)
  return result

## 上面部分可以封装在一个类中，然后在下面的主程序中直接调用find_rule函数

data = pd.read_excel('data/menu_orders.xls', header = None) #读取数据
print(u'
转换原始数据至0-1矩阵...')
ct = lambda x : pd.Series(1, index = x[pd.notnull(x)]) #转换0-1矩阵的过渡函数
b = map(ct, data.as_matrix()) #用map方式执行
data = pd.DataFrame(list(b)).fillna(0) #实现矩阵转换，空值用0填充
print(u'
转换完毕。')
del b #删除中间变量b，节省内存

support = 0.2 #最小支持度
confidence = 0.5 #最小置信度
ms = '---' #连接符，默认'--'，用来区分不同元素，如A--B。需要保证原始表格中不含有该字符

find_rule(data, support, confidence, ms)

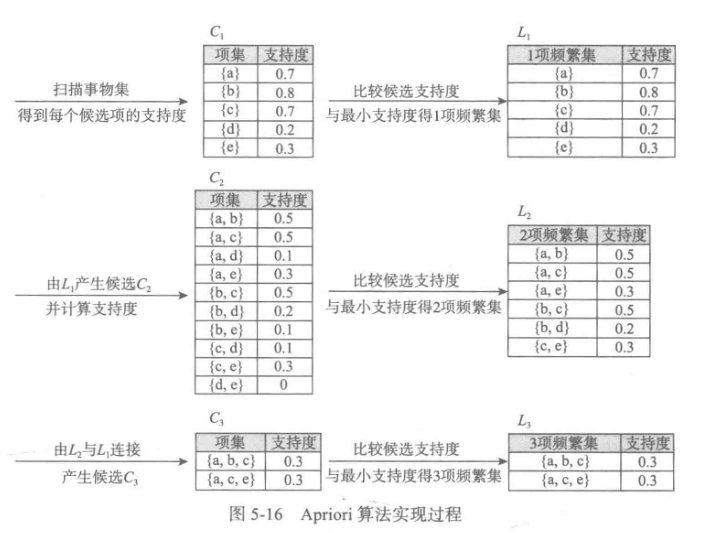
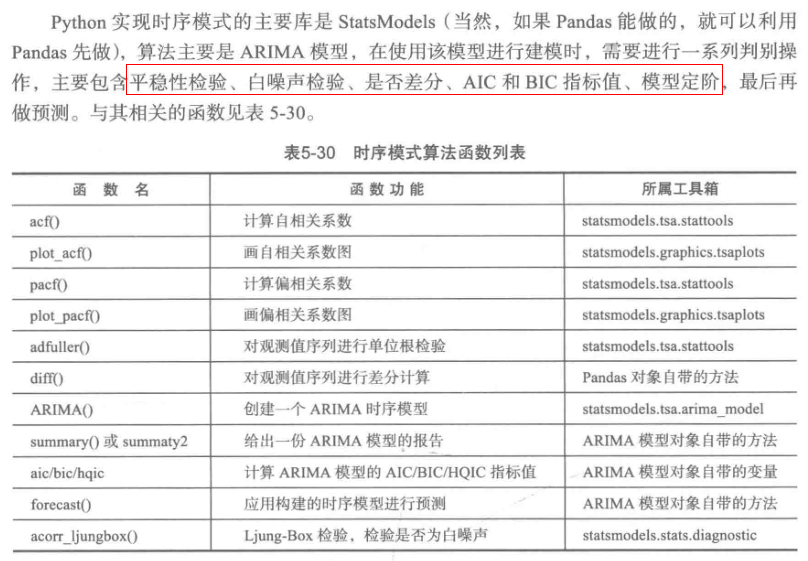
五、时序模式

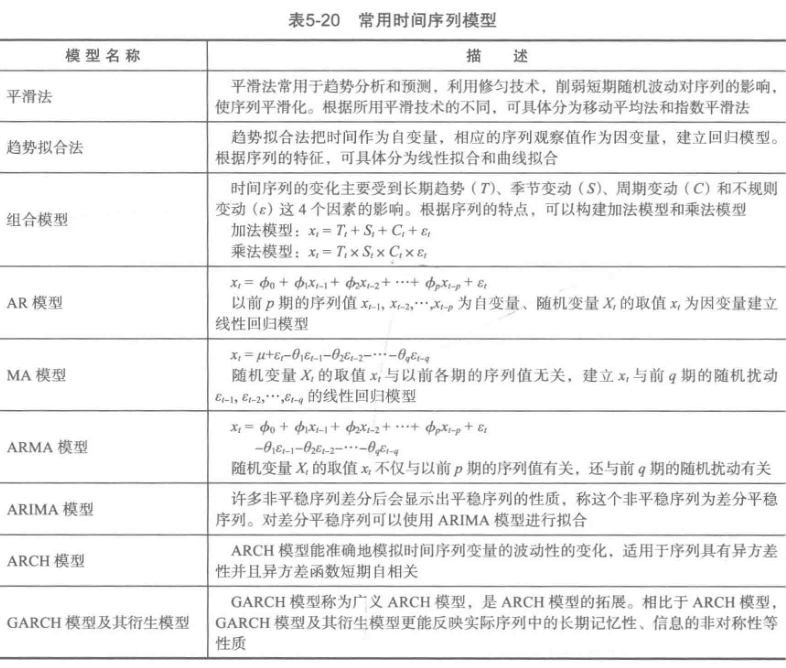
以下代码全程懵逼

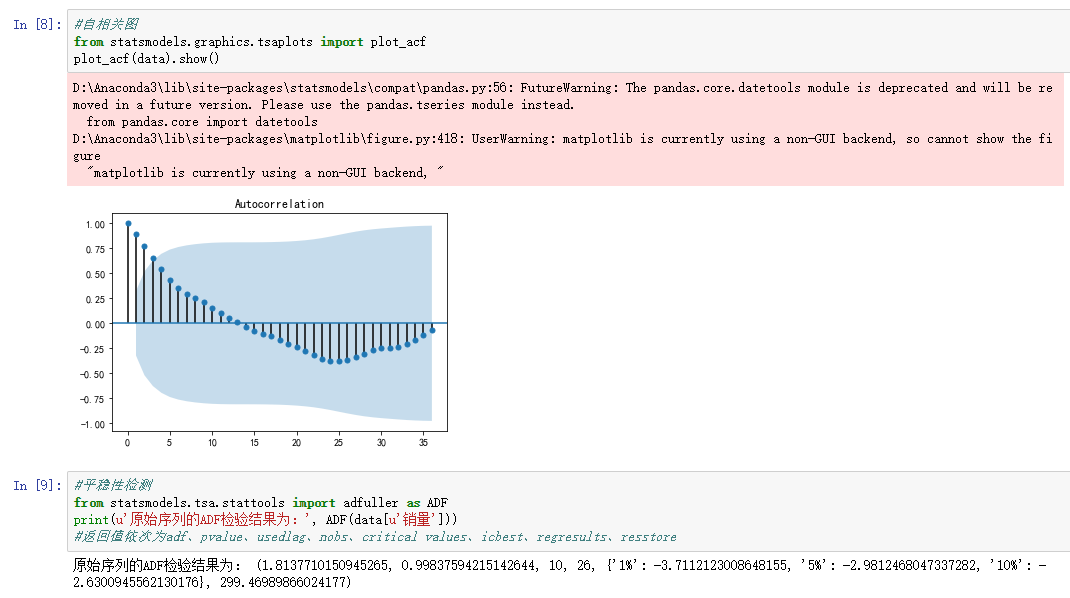
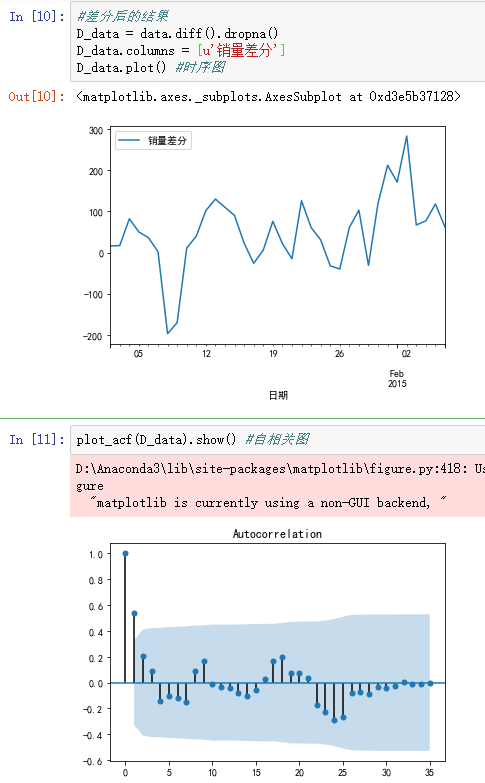
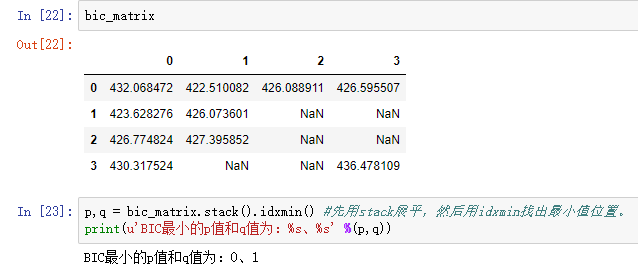
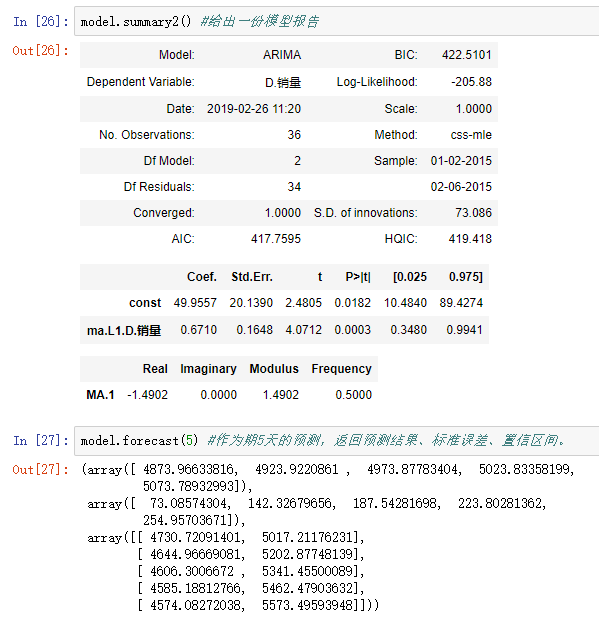
#arima时序模型
import matplotlib.pyplot as plt
import pandas as pd 
%matplotlib inline 
plt.rcParams['axes.unicode_minus']=False  #正常显示负号

#读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel('data/arima_data.xls', index_col = u'日期')
forecastnum = 5

#时序图
data.plot()

#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).show()

#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为：', ADF(data[u'销量']))
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

#差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #时序图
plot_acf(D_data).show() #自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).show() #偏自相关图
print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分'])) #平稳性检测

#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) #返回统计量和p值


from statsmodels.tsa.arima_model import ARIMA

data[u'销量'] = data[u'销量'].astype(float)
#定阶
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
  tmp = []
  for q in range(qmax+1):
    try: #存在部分报错，所以用try来跳过报错。
      tmp.append(ARIMA(data, (p,1,q)).fit().bic)
    except:
      tmp.append(None)
  bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix) #从中可以找出最小值

p,q = bic_matrix.stack().idxmin() #先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s、%s' %(p,q)) 
model = ARIMA(data, (p,1,q)).fit() #建立ARIMA(0, 1, 1)模型
model.summary2() #给出一份模型报告
model.forecast(5) #作为期5天的预测，返回预测结果、标准误差、置信区间。

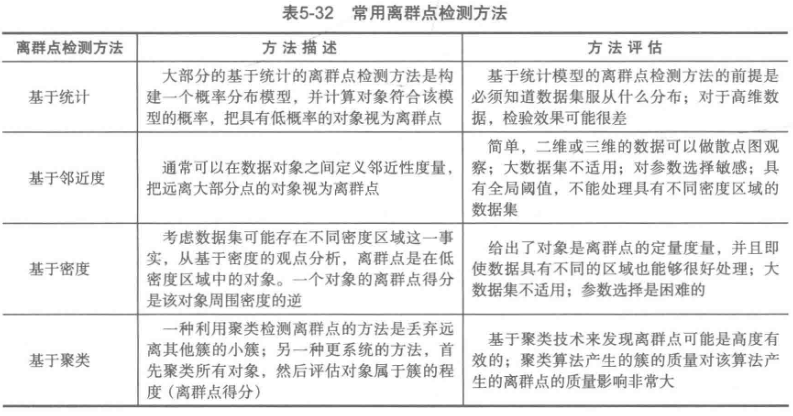
六、离群点检测

 

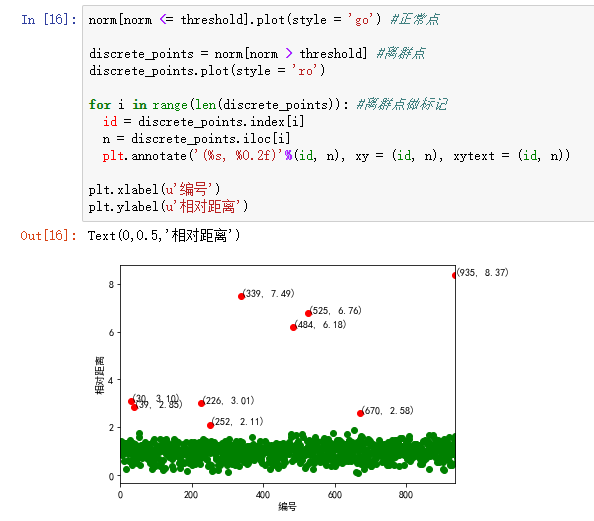
#使用K-Means算法聚类消费行为特征数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
%matplotlib inline 
plt.rcParams['axes.unicode_minus']=False  #正常显示负号

#参数初始化
k = 3 #聚类的类别
threshold = 2 #离散点阈值
iteration = 500 #聚类最大循环次数

data = pd.read_excel('data/consumption_data.xls', index_col = 'Id') #读取数据
data_zs = 1.0*(data - data.mean())/data.std() #数据标准化

model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration) #分为k类，并发数4
model.fit(data_zs) #开始聚类

#标准化数据及其类别
r = pd.concat([data_zs, pd.Series(model.labels_, index = data.index)], axis = 1)  #每个样本对应的类别
r.columns = list(data.columns) + [u'聚类类别'] #重命名表头

norm = []
for i in range(k): #逐一处理
  norm_tmp = r[['R', 'F', 'M']][r[u'聚类类别'] == i]-model.cluster_centers_[i]
  norm_tmp = norm_tmp.apply(np.linalg.norm, axis = 1) #求出绝对距离
  norm.append(norm_tmp/norm_tmp.median()) #求相对距离并添加
norm = pd.concat(norm) #合并

norm[norm <= threshold].plot(style = 'go') #正常点
discrete_points = norm[norm > threshold] #离群点
discrete_points.plot(style = 'ro')
for i in range(len(discrete_points)): #离群点做标记
  id = discrete_points.index[i]
  n = discrete_points.iloc[i]
  plt.annotate('(%s, %0.2f)'%(id, n), xy = (id, n), xytext = (id, n))
plt.xlabel(u'编号')
plt.ylabel(u'相对距离')
plt.show()

七、小结