概率是从高中就开始学习的内容,自然语言处理的学习中概率是常用的数学知识之一,但毕业多年,日常的工作学习中也很少用到,忘记了大半,也借此机会将基础知识复习一下。
概率:什么是概率?简单的理解,某一系列事件中某一事件发生的频率,或一系列事件中某一事件发生的可能性。
联合概率: P(AB),代表A和B都发生的可能性,就是联合概率。
条件概率:当某些事件发生时其它事件也发生的概率。我们将事件 B 发生时事件 A 也发生的条件概率写为 P(A | B)。设A,B 是两个事件,且A不是不可能事件,则称为在事件A发生的条件下,事件B发生的条件概率。

例:求一个月中阴天后下雨的概率P(雨/阴)
已知:一个月中阴天的天数大概有5天P(阴)=1/6,阴天且下雨的天数为4天P(阴.雨)=2/15
P(阴)=1/6,P(阴.雨)=2/15
P(雨/阴)= P(阴.雨)/P(阴)=4/5
相依事件与独立事件:如果一个事件的概率不以任何方式影响另一个事件,则该事件被称为独立事件,反之则为相依事件。P(A | B) = P(A)。这就意味着事件 A 独立于事件 B。
贝叶斯概率论(贝叶斯定理)
贝叶斯可以作为一种理解概率的替代方法。贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。

例:
求一个月中阴天后下雨的概率P(雨/阴)
已知:一个月中阴天的天数大概有5天P(阴)=1/6,下雨天大概有6天P(雨)=1/5,在下雨前天阴的概率为P(阴/雨)=4/5,那么:P(雨/阴)= P(阴/雨)* P(雨)/ P(阴)=1/5*4/5 / 1/6=24/25=96%
连续和离散概率分布
概率分布可分为两种:离散分布用于处理具有有限值的随机变量,如投掷硬币和伯努利分布的情形。离散分布是由所谓的概率质量函数(PMF)定义的,连续分布用于处理连续的(理论上)有无限数量的值的随机变量。想想用声音传感器测量的速度和加速度。连续分布是由概率密度函数(PDF)定义的。
这两种分布类型在数学处理上有所不同:通常连续分布使用积分 ∫ 而离散分布使用求和Σ。以期望值为例:
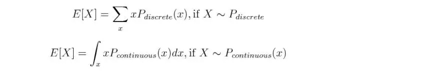
离散型随机变量分布常见的有伯努利分布(Bernoulli Distribution)、二项分布(Binomial Distribution)、泊松分布(Poisson Distribution)等,而常见的连续型随机变量分布包括均匀分布(Uniform Distribution)、指数分布(Exponential Distribution)、正态分布等。
1、伯努利分布
从最简单的分布伯努利分布开始。
伯努利分布只有两种可能的结果,1(成功)和0(失败)。因此,具有伯努利分布的随机变量X可以取值为1,也就是成功的概率,可以用p来表示,也可以取值为0,即失败的概率,用q或1-p来表示。
概率质量函数由下式给出:px(1-p)1-x, 其中x € (0, 1)。它也可以写成:
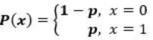
伯努利分布的随机变量X的期望值如为:
E(X) = 1*p + 0*(1-p) = p
随机变量与二项分布的方差为:
V(X) = E(X²) – [E(X)]² = p – p² = p(1-p)
2、二项分布
掷硬币时,当掷完第一次,我们可以再掷一次,也就是存在多个伯努利试验。第一次为正不代表以后也会为正。那么设一个随机变量 X,它表示我们投掷为正面的次数。X 可能会取什么值呢?在投掷硬币的总次数范围内可以是任何非负整数。
如果存在一组相同的随机事件,即一组伯努利试验,在上例中为连续掷硬币多次。那么某随机事件出现的次数即概率服从于二项分布,也称为多重伯努利分布。
任何一次试验都是互相独立的,前一次试验不会影响当前试验的结果。两个结果概率相同的试验重复 n 次的试验称为多次伯努利试验。二项分布的参数为 n 和 p,n 是试验的总次数,p 是每一次试验的成功概率。
根据以上所述,一个二项分布的性质为:
1. 每一次试验都是独立的;
2. 只有两个可能的结果;
3. 进行 n 次相同的试验;
4. 所有试验中成功率都是相同的,失败的概率也是相同的。
二项分布的数学表达式为:

3、泊松分布
如果你在一个呼叫中心工作,一天内会接到多少次呼叫呢?多少次都可能!在呼叫中心一天能接到多少次呼叫可以用泊松分布建模。这里有几个例子:
1. 一天内医院接到的紧急呼叫次数;
2. 一天内地方接到的偷窃事件报告次数;
3. 一小时内光顾沙龙的人数;
4. 一个特定城市里报告的自杀人数;
5. 书的每一页的印刷错误次数。
现在你可以按相同的方式构造很多其它的例子。泊松分布适用于事件发生的时间和地点随机分布的情况,其中我们只对事件的发生次数感兴趣。泊松分布的主要特点为如下:
1. 任何一个成功事件不能影响其它的成功事件;
2. 经过短时间间隔的成功概率必须等于经过长时间间隔的成功概率;
3. 时间间隔趋向于无穷小的时候,一个时间间隔内的成功概率趋近零。
在泊松分布中定义的符号有:
λ是事件的发生率;
t 是事件间隔的长度;
X 是在一个时间间隔内的事件发生次数。
设 X 是一个泊松随机变量,那么 X 的概率分布称为泊松分布。以µ表示一个时间间隔 t 内平均事件发生的次数,则 µ=λ*t;
X 的概率分布函数为:

泊松分布的概率分布图示如下,其中µ为泊松分布的参数:
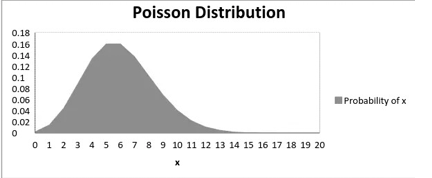
下图展示了均值增加时的分布曲线的变化情况:
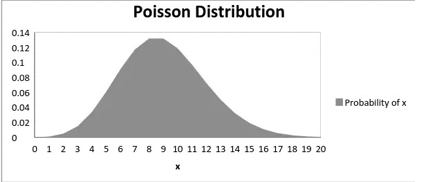
如上所示,当均值增加时,曲线向右移动。泊松分布的均值和方差为:
均值:E(X) = µ
方差: Var(X) = µ
4、均匀分布
对于投骰子来说,结果是1到6。得到任何一个结果的概率是相等的,这就是均匀分布的基础。与伯努利分布不同,均匀分布的所有可能结果的n个数也是相等的。
花店每天销售的花束数量是均匀分布的,最多为40,最少为10。我们来计算一下日销售量在15到30之间的概率。
日销售量在15到30之间的概率为(30-15)*(1/(40-10)) = 0.5
同样地,日销售量大于20的概率为 = 0.667
5、指数分布
在深度学习中,我们经常会需要一个在 x=0 处取得边界点 (sharp point) 的分布。为了实现这一目的,我们可以使用指数分布(exponential distribution):
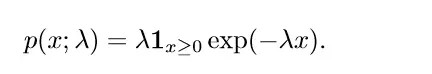
指数分布使用指示函数 (indicator function)1x≥0,以使当 x 取负值时的概率为零。
其中 λ >0 为概率密度函数的参数。随机变量 X 服从于指数分布,则该变量的均值可表示为 E(X) = 1/λ、方差可以表示为 Var(X) = (1/λ)^2。如下图所示,若λ较大,则指数分布的曲线下降地更大,若λ较小,则曲线越平坦。如下图所示:
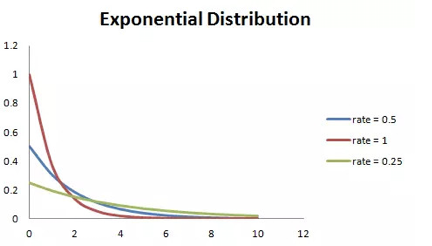
以下是由指数分布函数推导而出的简单表达式:
P{X≤x} = 1 – exp(-λx),对应小于 x 的密度函数曲线下面积。
P{X>x} = exp(-λx),代表大于 x 的概率密度函数曲线下面积。
P{x1<X≤ x2} =exp(-λx1)-exp(-λx2),代表 x1 点和 x2 点之间的概率密度函数曲线下面积。
6、正态分布(高斯分布)
最常用的分布就是正态分布(normal distribution),也称为高斯分布(Gaussian distribution)。因为该分布的普遍性,尤其是中心极限定理的推广,一般叠加很多较小的随机变量都可以拟合为正态分布。正态分布主要有以下几个特点:
1. 所有的变量服从同一均值、方差和分布模式。
2. 分布曲线为钟型,并且沿 x=μ对称。
3. 曲线下面积的和为 1。
4. 该分布左半边的精确值等于右半边。
正态分布和伯努利分布有很大的不同,然而当伯努利试验的次数接近于无穷大时,他们的分布函数基本上是相等的。
若随机变量 X 服从于正态分布,那么 X 的概率密度可以表示为:
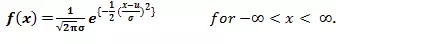
随机变量 X 的均值可表示为 E(X) = µ、方差可以表示为 Var(X) = σ^2。其中均值µ和标准差σ为高斯分布的参数。
随机变量 X 服从于正态分布 N (µ, σ),可以表示为:
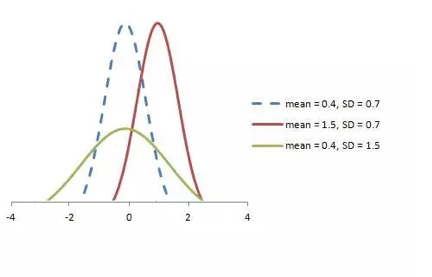
标准正态分布可以定义为均值为 0、方差为 1 的分布函数,以下展示了标准正态分布的概率密度函数和分布图:

参考:
https://36kr.com/p/5094400
https://www.cnblogs.com/coloz/p/10709824.html