一、什么是德.摩根定律
德摩根定律有多种形式,在集合中的形式如下:

我们可以用生活中的例子也来理解该定理,假设某学校举办运动会,(A) 代表“去跑步”的同学,(B) 代表“去跳远”的同学,(Acup B) 表示“去跑步或跳远”的同学,所以有:

而(A cap B) 表示“既跑步又跳远”,所以有:

二、怎么记忆摩根定律
理解归理解,德摩根定律看上去还是有点复杂,可以通过下面方法来记忆,就是头顶上的帽子断开时,中间的符号要翻转:
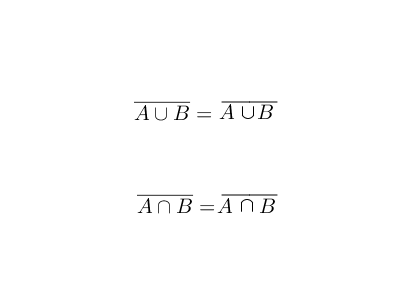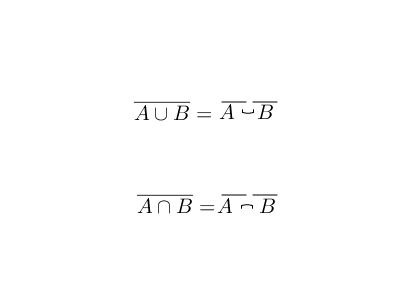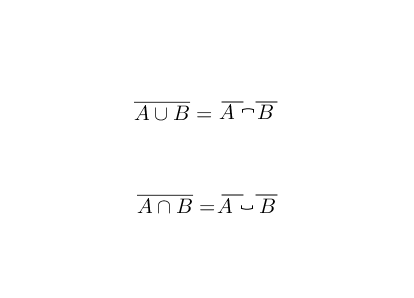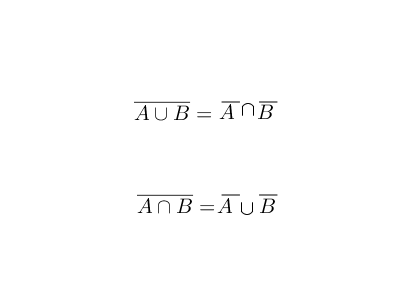
德摩根定律拓展到多个事件上也是成立的,记忆方法也是一样的:

三、小试牛刀
化简下面的逻辑表达式:
1、 ((A+B)(A+C))
(=AA+AC+AB+BC) 分配律
(=A+AC+AB+BC) (AA=A)
(=A(1+C+B)+BC) 反向使用分配律
(=A+BC) (A+1=1)
结论:((A+B)(A+C)=A+BC)
2、(AB+overline AC+BC)
(=AB+ overline AC+BC(A+ overline A)) 依据:(A+ overline A =1)
(=AB+ overline AC+ ABC+overline ABC) 分配律
(=AB+ABC+overline AC+overline ABC) 结合律
(=AB(1+C) + overline AC(1+B)) 反向分配律
(=AB+ overline AC) (A+1=1)
结论:(AB+overline AC+BC = AB+ overline AC)
3、(overline {A overline B +overline {AC}})
(=(overline A + B)(A+C)) 摩根定律
(=overline AA+ overline A C+ AB+BC) 分配律
(=AB+ overline AC+BC) (A overline A=0)
(=AB+ overline AC+BC(A+ overline A)) 依据:(A+ overline A =1)
(=AB+ overline AC+ ABC+overline ABC) 分配律
(=AB+ABC+overline AC+overline ABC) 结合律
(=AB(1+C) + overline AC(1+B)) 反向分配律
(=AB+ overline AC) (A+1=1)
结论:(overline {A overline B +overline {AC}} = AB+ overline AC)
4、(!((x<=0 || x>5) && (y<=0 || y>10))
设(X= (x<=0)),(Y=(x>5)),(A=(y=0)),(B=(y>10))
原式=(overline{(X+Y)(A+B)})
(=overline{X+Y}+ overline {A+B}) 摩根定律
(=overline X cdot overline Y + overline A cdot overline B) 摩根定律
也就是(x>0 && x<=5 || y>0 & & y<=10)