P2638 安全系统

题目传送门

一、问题重述

有两种球，分别是黑球（信号 0）和 红球（信号 1），相同类别的球之间没有区别。现在有 (n) 个各不相同的盒子（储存区），要把 (a) 个黑球和 (b) 个红球放进这些盒子里,求方案总数。

每个盒子可以装任意多球，也可以不装。并且以上 (a+b)个球不需要全部放进盒子里，甚至可以不放任何球进盒子里。

二、问题分析

• 可以全部放入箱子，也可以不全部放入箱子，也可以全都不放入箱子，这样不好讨论。我们思考在确定黑球和红球数量下的求法：
  (f(n,i,j))代表在(n)个箱子，(i)个黑球，(j)个红球的情况。其中 (0<=i<=a,0<=j<=b);
  所有情况的办法和就是答案：加法原理！
  (ans= f(n,0,0)+f(n,0,1)+...+f(n,0,b)+f(n,1,0)+f(n,1,1)+...+f(n,1,b) +... +f(n,a,0)+f(n,a,1)+...+f(n,a,b))

数学公式描述：

$large ans= sumlimits_{i=0}^asumlimits_{j=0}^bf(n,i,j)$

• 如果我们知道(f(n,i,j))怎么求，就可以通过双重循环得到结果 。

  讨论一下(f(n,i,j))这一表示法怎么求，注意：红球和黑球的放法是不相关的，就是乘法原理(f(n,i,j)=g(n,i)*g(n,j))

  那么(g(n,i))怎么求呢？换句人话就是 在(n)个盒子里放(i)个黑球，有几种放法。

插板法

因为每个盒子里可以选择放，也可以选择不放，不好直接想，我们退一步，先想一下每个盒子至少放一个的情况下，有多少种放法，再考虑迁移到这个问题上来。

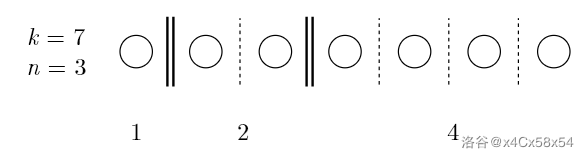
每个盒子里至少放一个黑球，(k)个黑球有(k-1)个缝隙，需要放入(n-1)个插板，就是(large C_{k-1}^{n-1})

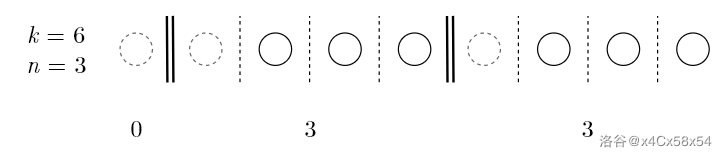
那如果可以不放呢？就是假设再有(n)个黑球，每个箱子里放一个，用完再取走。就是(k+n)个黑球，(k+n-1)个缝隙，还是(n-1)个插板，方案数就是(large C_{k+n-1}^{n-1})

• 核心代码：

    for(int i = 0; i <= a; i++)
        for(int j = 0; j <= b; j++)
            ans += C[n+i-1][n-1] * C[n+j-1][n-1];

• 再来看一下数据范围。这里的组合数需要算到多大呢？容易看出最大总元素数（就是(C) 的那个下标）是 (n+max(a, b)-1)。
  根据题给范围，我们最多需要算到(C(49,k)).可以验证，这不需要高精度，但是一定要开 (unsigned long long)！切记！

三、完整代码

#include <bits/stdc++.h>

//https://www.luogu.com.cn/blog/x4Cx58x54/solution-p2638
//经典题

using namespace std;
typedef unsigned long long ULL;
int n, a, b;
ULL ans;

//求组合数的优化后办法
//优点：从1开始除和乘，可以防止过早溢出和除法除不尽
ULL C(int n, int m) {
    ULL sum = 1;
    for (int i = 1; i <= m; i++)
        sum = sum * (n - m + i) / i;
    return sum;
}

int main() {
    cin >> n >> a >> b;
    for (int i = 0; i <= a; i++)
        for (int j = 0; j <= b; j++)
            ans += C(n + i - 1, n - 1) * C(n + j - 1, n - 1);

    cout << ans << endl;
    return 0;
}