AcWing 849. Dijkstra求最短路 I

题目传送门

一、算法思路

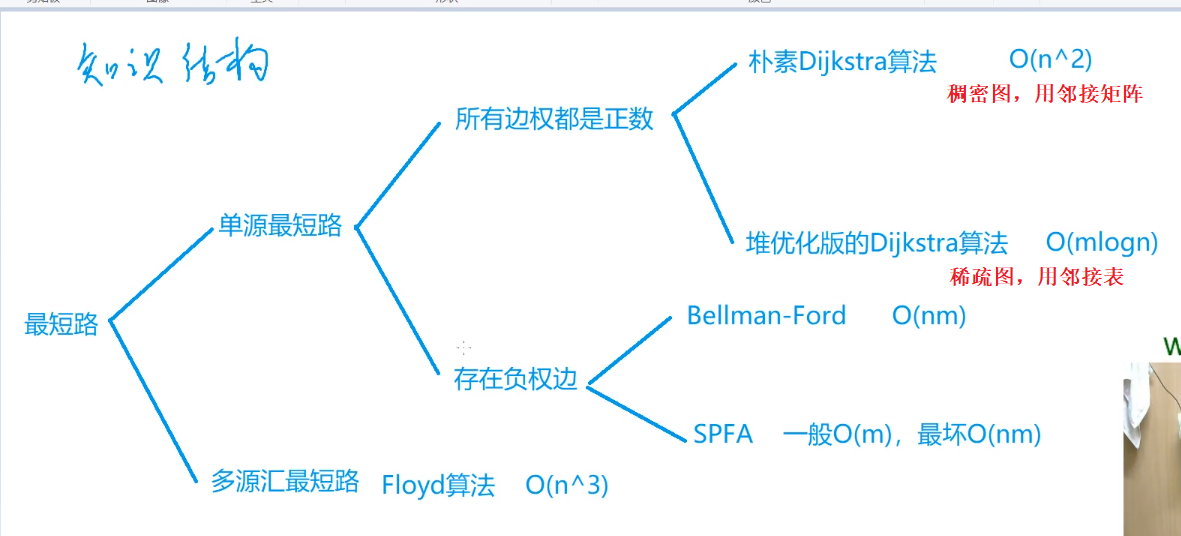
(Dijkstra) 的整体思路比较清晰,即进行(n)次迭代去确定每个点到起点的最小值,最后输出的终点的即为我们要找的最短路的距离。

按照这个思路除了存储图外我们还需要存储两个量:

dist[n]   //用于存储每个点到起点的最短距离
st[n]     //用于在更新最短距离时 判断当前的点的最短距离是否确定 是否需要更新

每次迭代的过程中我们都先找到当前未确定的最短距离的点中距离最短的点,（至于为什么是这样那么这就涉及到(Dijkstra)算法的具体数学证明了 有兴趣的同学可以百度一下）

int t=-1;                                 //将t设置为-1 因为Dijkstra算法适用于不存在负权边的图
for(int j=1;j<=n;j++){
    if(!st[j]&&(t==-1||dist[t]>dist[j])    //该步骤即寻找还未确定最短路的点中路径最短的点
        t=j;
}

通过上述操作当前我们的(t)代表就是剩余未确定最短路的点中路径最短的点,而与此同时该点的最短路径也已经确定我们将该点标记:

st[t]=true;

然后用这个去更新其余未确定点的最短距离

for(int j=1;j<=n;j++)
    dist[j]=min(dist[j],dist[t]+g[t][j]);

//这里可能有同学要问j如果从1开始的话 会不会影响之前已经确定的点的最小距离
//但其实是不会 因为按照我们的Dijkstra算法的操作顺序 先确定最短距离的点的距离已经比后确定的要小 所以不会影响
//当然你也可以在循环判断条件里加上if(!st[i])
//这里j从1开始只是为了代码的简洁

进行(n)次迭代后最后就可以确定每个点的最短距离,然后再根据题意输出相应的要求的最短距离。

二、C++ 代码

#include <bits/stdc++.h>

using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 510;//500个点，开大一点，用邻接矩阵来写，稠密图
int n, m;

int g[N][N];  // 稠密图,邻接矩阵
int dist[N];  // 记录每个节点距离起点的距离
bool st[N];   // true表示已经确定最短路 属于s集合

// 求1号点到n号点的最短路，如果不存在则返回-1
int dijkstra() {
    //所有节点距离起点的距离初始化为无穷大
    memset(dist, 0x3f, sizeof dist);
    //起点距离自己的距离为零
    dist[1] = 0;
    // n-1次循环，而非n次循环(因为1节点自身已确定)
    for (int i = 1; i <= n - 1; i++) {
        // 在还未确定最短路的点中，寻找距离最短的点
        int t = -1;
        //-1代表首个未使用过的点，是不是最短不知道，先放里，作为首个猴王,后面如果有距离更短的会替换掉。
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        // 用t更新其他点的距离
        for (int j = 1; j <= n; j++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
        //加入到s集合中
        st[t] = true;
    }
    // 如果起点到达不了n号节点，则返回-1
    if (dist[n] == INF) return -1;
    // 返回起点距离n号节点的最短距离
    return dist[n];
}

int main() {
    //输入优化
    ios::sync_with_stdio(false);
    cin >> n >> m;
    //初始化
    memset(g, 0x3f, sizeof g);
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c); //图中可能存在重边和自环.如果存在重边，那么以最小的那条为最终的数据
    }
    //调用迪卡斯彻算法
    int t = dijkstra();
    printf("%d
", t);
    return 0;
}