一、题目描述
给定 (n) 个 (0) 和 (n) 个 (1),它们将按照某种顺序排成长度为 (2n) 的序列,求它们能排列成的所有序列中,能够满足任意前缀序列中 (0) 的个数都不少于 (1) 的个数的序列有多少个。答案对 (10^9+7) 取模。
数据范围:(1≤n≤10^5)
组合计数,卡特兰数
二、解题思路
将 (01) 序列置于坐标系中,起点定于原点。若 (0) 表示向右走,(1) 表示向上走,那么任何前缀中 (0) 的个数不少于 (1) 的个数就转化为,路径上的任意一点,横坐标大于等于纵坐标。题目所求即为这样的合法路径数量。
下图中,表示从 ((0,0)) 走到 ((n,n)) 的路径,在绿线及以下表示合法,若触碰红线即不合法。
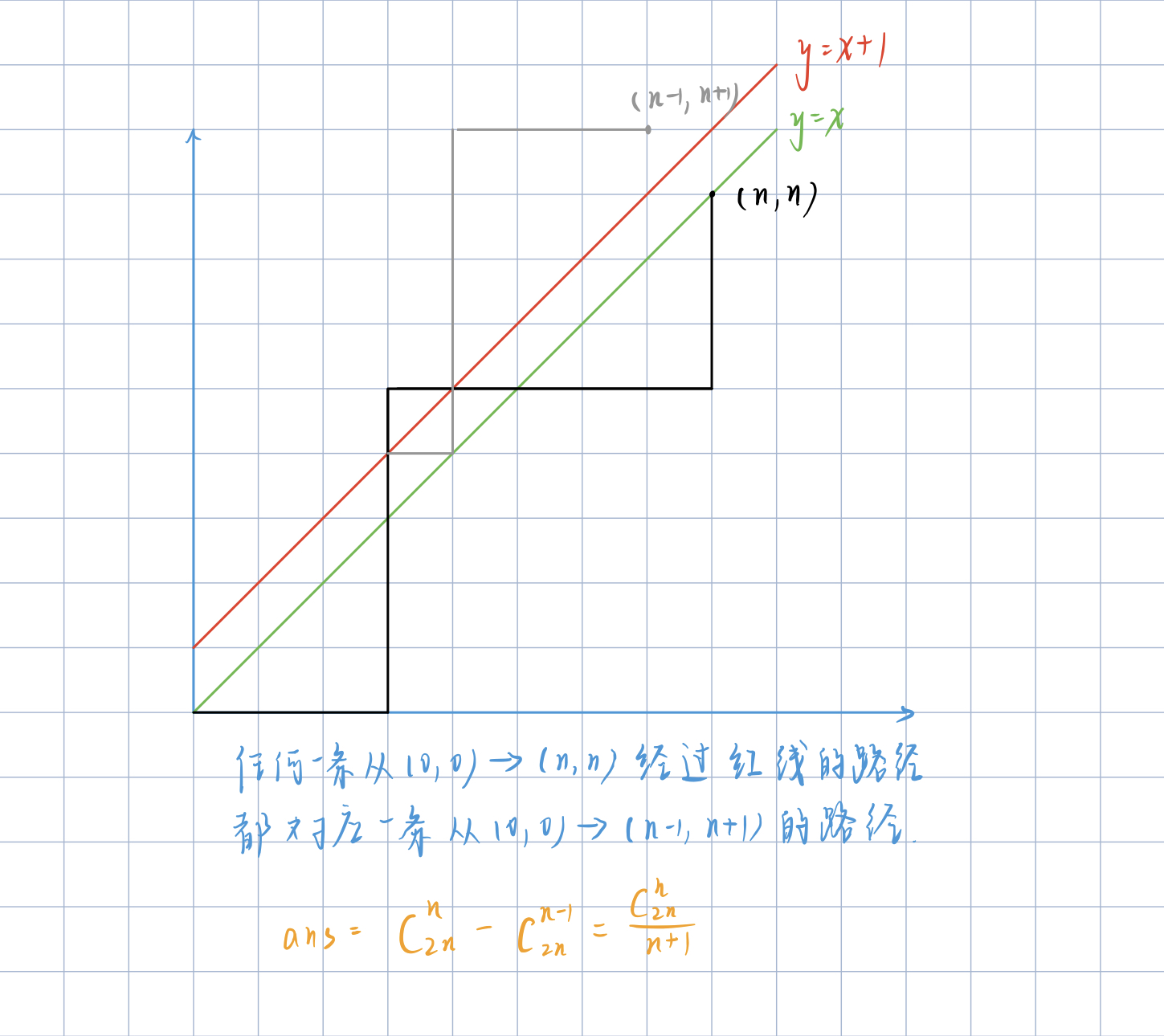
由图可知,任何一条不合法的路径(如黑色路径),都对应一条从 ((0,0)) 走到 ((n−1,n+1)) 的一条路径(如灰色路径)。而任何一条 ((0,0)) 走到 ((n−1,n+1)) 的路径,也对应了一条从 ((0,0)) 走到 ((n,n)) 的不合法路径。
答案如图,即卡特兰数。
三、举个栗子
假设(n=6):
1、方案总数
从((0,0))到((6,6))共有多少种走法
因为从((0,0))到((6,6)) 共需要向上共走(6)步,向右共走(6)步,一共(12)步。
每步两种选择,向上或向右,共(2)种选择。
如果在其中某(6)个步骤中选择向上走,那么剩下的(6)个步骤就是向右走。
向上走的方案数就是(LARGE C_{12}^6),向上的方案数定了,其它的步骤只能是向右的,最终的方案数是(LARGE C_{12}^6) 。
2、红线的用途
红线是根据题目要求的画出来的,也是卡特兰数的精华。在红线以下的路径是合法的,红线就是高压线,不能超过红线!因为题目要求任何时刻,(0)要比(1)多,也就是向右的个数要比向上的多!绿色线是相等,一旦达到或超过红线,都是不可以的!
比如上面图中的黑色线,就是一条不符合要求的线,因为有部分超过了红线。 如果我们计算出来有多少条这样的黑线,从总数中减出去,就是合法的方案数。
3、黄线的数量计算
每一条黑线,一旦越过红线的部分,都可以根据红线做轴对称,画出对称的灰线。这样,所有到((6,6))的黑线,都可以找到一条到((5,7))的灰线,换句话说,我们只要计算出从((0,0))到((5,7))的方案数,也就是到((0,0))到((6,6))的越红线(也就是黑线)的方案数个数。从((0,0))到((5,7))的方案数:(LARGE C_{12}^5)
4、合法方案数
(C_{12}^{6} - C_{12}^{5})
这是以((6,6))为例子,泛化后就是 $ LARGE C_{2n}^{n} - C_{2n}^{n-1}= frac{C_{2n}^{n}}{n+1}$
$ large = frac{2n imes (2n-1) imes ... imes (n+1) }{n imes (n-1) imes (n-2) imes ... imes 1} mod (m) imes inv(n+1)$
$ = 2n imes (2n-1) imes ... imes (n+1) imes inv(n+1) imes inv(n) imes inv(n-1) imes inv(n-2) imes ... mod(m)$
四、C++ 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod = 1e9 + 7;
int n;
int qmi(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = (LL) res * a % mod;
b >>= 1;
a = (LL) a * a % mod;
}
return res;
}
int main() {
//优化输入
ios::sync_with_stdio(false);
cin >> n;
int res = 1;
//计算C(2n,n) mod 1e9+7
for (int i = 2 * n; i > n; i--) res = (LL) res * i % mod;
for (int i = n + 1; i; i--) res = (LL) res * qmi(i, mod - 2) % mod;
cout << res << endl;
return 0;
}
五、记忆卡特兰数特征
数列的前几项为:(1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862)