一、核心思想
1、先放横着的,再放竖着的。
2、总方案数等于只放横着的小方块的合法方案数。
为什么呢?因为如果把横着的全部放完之后,其它的空用竖着的来放就行啦。如果横的放完了,竖着的方案数是唯一的。
那如何判断方案是否合法?
当前摆完横着的小方块之后,所有剩余的位置,如果能填充满竖着的小方块就是合法,否则不合法。进一步思考知道:可以按列来看,每一列只要所有连续的空着的小方块个数是偶数个,就可以用竖着的去填充满。如果存在奇数个连续空着的小方块,必然填充不满。
二、状态表示
这是一道动态规划的题目,并且是一道状态压缩的\(dp\):用一个\(N\)位的二进制数,每一位表示一个物品,\(0/1\)表示不同的状态。因此可以用\(0 → 2^N − 1\) ( \(N\) 二 进 制 对 应 的 十 进 制 数 )中的所有数来枚举全部的状态。
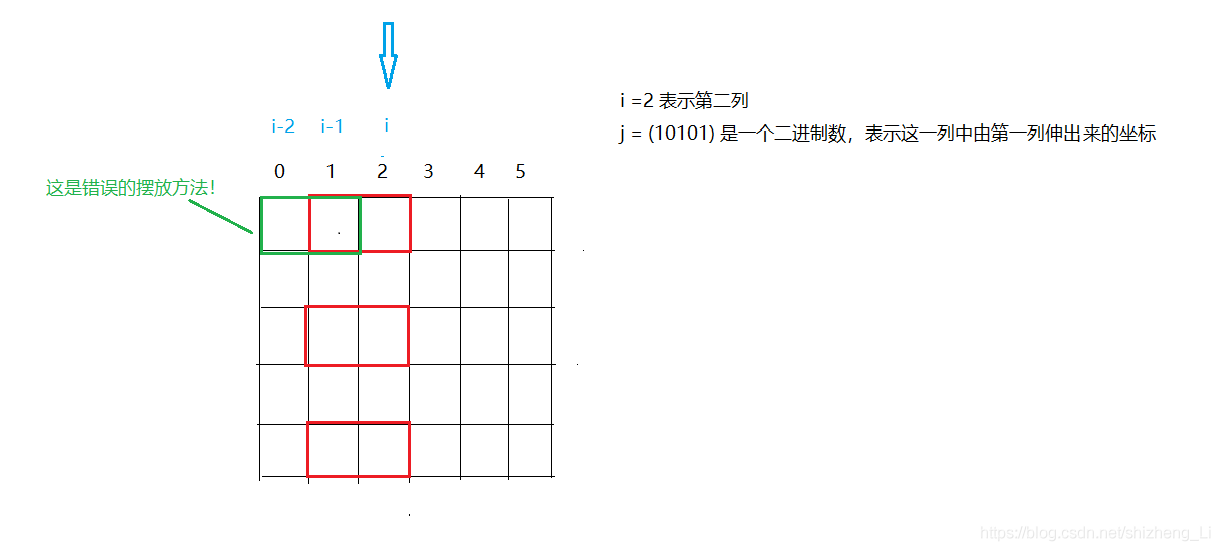
\(f[i][j]\) 表示:已经将前 \(i -1\) 列摆好,且从第\(i − 1\)列伸出到第\(i\)列的状态是\(j\)的所有情况。其中\(j\)是一个二进制数,用来表示哪一行的小方块是横着放的,其位数和棋盘的行数一致。 请看下面的释义:

解释:上图中 \(i=2\),\(j =10101\)(二进制数,但是存的时候用十进制 ) 所以这里的\(f[i][j]\) 表示的是所有前\(i-1\)列摆完之后,从第 \(i-1\)列伸到第\(i\)列的状态是\(10101\)(第\(1\)行伸出来,第\(3\)行伸出来,第\(5\)行伸出来,其他行没伸出来)的方案数。
三、状态转移
第\(i-1\)列的某种状态,与第\(i\)列的某种状态之间,是可能存在转换关系的,也可能是不存在转换关系的。
讨论一下什么情况下会不存在转换关系:
(1)、状态冲突
如果\(i-2\)想在当前行“伸出”一个小方格,而\(i-1\)列也想向下一列“伸出”一个小方格,就是冲突。
对应的代码为(i & j ) ==0 ,表示 \(i\)和\(j\)没有\(1\)位相同,即没有\(1\)行有冲突。此处的位运算大大提高了两种状态冲突检测的效率!,如果不用位运算,循环一个是跑不了的!
(2)、后序状态无效
是不是状态不冲突就可以转化了呢?不是的,举个栗子吧:两种状态不冲突:
\(i-2\)列有一个状态:\(00100\),\(i-1\)列有一个状态:\(01010\),它们两个之间是没有重叠的,不违反上面的第一条规则,但依然是有问题的:
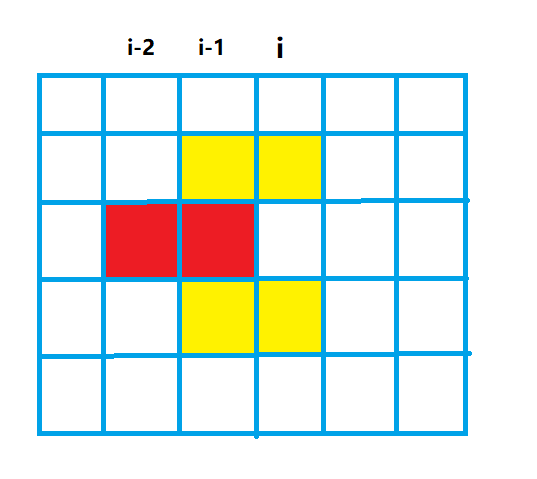
它会造成\(i-1\) 列无法继续用竖着的小方格填充满!!!
那该如何避免这个问题呢?其实就是“尝试”两个状态叠加后再判断目标状态是不是满足连续奇数个\(0\)。
四、实现代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 12;
const int M = 1 << N;
int n, m;
LL f[N][M]; //动态规划的状态数组
vector<int> state[M];//对于每个状态而言,能转转移到它的状态有哪些,预处理一下(二维数组)
int st[M]; //某种状态是否合法,就是是不是存在奇数个连续0
int main() {
//优化输入
ios::sync_with_stdio(false);
while (cin >> n >> m, n || m) {
//预处理1:计算每个二进制描述态是否合法,有奇数个连续0非法
for (int i = 0; i < 1 << n; i++) {
int cnt = 0; //连续0的个数
st[i] = 1; //默认此态是合法的
for (int j = 0; j < n; j++)//遍历此状态的每一个二进制位
if (i >> j & 1) { //如果本位是1
if (cnt & 1) {
st[i] = 0;//此时,连续0发生了中断,需要判断是不是奇数个连续0
break;
}
//重新开始计数
cnt = 0;
} else cnt++;//连续0个数++
//最后一个cnt++后,依然可能有连续奇数个0
if (cnt & 1) st[i] = 0;
}
//预处理2:枚举每个状态而言,它可能是从哪些有效状态转化而来
for (int i = 0; i < 1 << n; i++) {
//多组数据,每次预处理时清空一下
state[i].clear();
//状态i中以从哪些状态转化而来?
for (int j = 0; j < 1 << n; j++)
if ((i & j) == 0 && st[i | j])
state[i].push_back(j);
}
//多组数据,每次清零
memset(f, 0, sizeof f);
//动态规划
f[0][0] = 1;//出发点只有一种方案
//遍历每一列
for (int i = 1; i <= m; i++)
//遍历第i列的所有状态j
for (int j = 0; j < 1 << n; j++)
//遍历第i-1列的所有状态k
for (auto k: state[j])
f[i][j] += f[i - 1][k];
//输出结果
cout << f[m][0] << endl;
}
return 0;
}
五、代码解读
1、预处理非奇数连续零状态
#include <bits/stdc++.h>
using namespace std;
const int N = 12;
int st[N];
int n = 5;
int main() {
//计算每个二进制描述态是否合法,有奇数个连续0非法
for (int i = 0; i < 1 << n; i++) {
int cnt = 0; //连续0的个数
st[i] = 1; //默认此态是合法的
for (int j = 0; j < n; j++)//遍历此状态的每一个二进制位
if (i >> j & 1) { //如果本位是1
if (cnt % 2) st[i] = 0;//此时,连续0发生了中断,需要判断是不是奇数个连续0
//重头计数
cnt = 0;
//本状态判断完毕,已经判断为非法状态,不必继续
continue;
} else cnt++;//连续0个数++
//最后一段二进制位0的个数是否为奇数
if (cnt % 2) st[i] = 0;
//输出每个状态是否合法
for (int j = 0; j < n; j++) {
printf("%d ", i >> j & 1);
}
printf(" 是否合法:%d\n", st[i]);
}
return 0;
}
2、预处理状态之间转化关系
(1) i & j ==0 同一列的每一行都不能同时探出小方格,那样会有重叠。
(2) 解释一下st[i | j]
已经知道\(st[]\)数组表示的是这一列有没有连续奇数个\(0\)的情况,我们要考虑的是第\(i-1\)列(第\(i-1\)列是这里的主体)中从第\(i-2\)列横插过来的,还要考虑自己这一列(\(i-1\)列)横插到第\(i\)列的,比如 第\(i-2\)列插过来的是\(k=10101\),第\(i-1\)列插出去到第\(i\)列的是 \(j =01000\),那么合在第\(i-1\)列,到底有多少个\(1\)呢?自然想到的就是这两个操作共同的结果:两个状态或。 j | k = 01000 | 10101 = 11101,最终的这个状态叠加和,是用来检查是不是存在奇数个\(0\)的期待状态值。
3、最终方案数
总共\(m\)列,我们假设列下标从\(0\)开始,即第\(0\)列,第\(1\)列……,第\(m-1\)列。根据状态表示\(f[i][j]\) 的定义,我们答案是什么呢? 请读者返回定义处思考一下。答案是\(f[m][0]\), 意思是前\(m-1\)列全部摆好,且从第\(m-1\)列到\(m\)列状态是\(0\)(意即从第\(m-1\)列到第\(m\)列没有伸出来的)的所有方案,即整个棋盘全部摆好的方案。