一、题目解析
题目描述
给定 \(n\) 个正整数:\(a_1,a_2,⋯,a_n\)
从中选出若干个数,使得他们的和为 \(m\)
求最终的 方案数
分析
对于本题我们可以把每个 正整数 看作是一个 物品
正整数 的值就是 物品 的 体积
我们方案选择的 目标 是最终 体积 恰好为 \(m\) 时的 方案数
于是本题就变成了** 01背包求解方案数** 的问题了
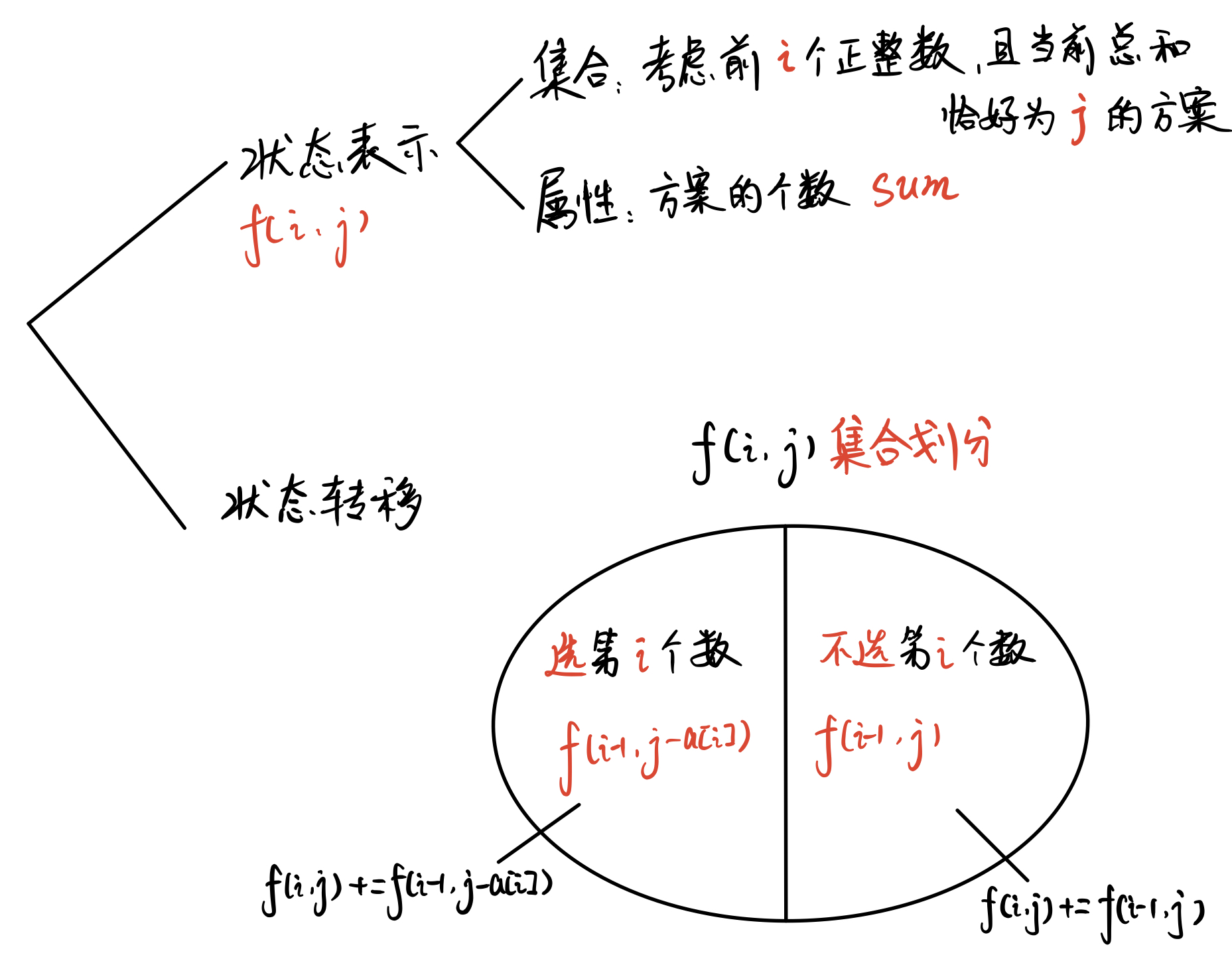
闫氏DP分析法
初始状态:f[0][0]
目标状态:f[n][m]
时间复杂度:\(O(n×m)\)
二、二维实现代码
#include <bits/stdc++.h>
using namespace std;
/**
二维数组+动态规划
状态转移方程:
1. 不选i:f[i][j] = f[i-1][j]
2. 选i: f[i][j] = f[i-1][j-v[i]]
所以总的方案数就1和2的和,注意:因为体积为0时,即j=0时,是存在一种方案的:f[0][0] = 1
*/
const int N = 110;
const int M = 10010;
int n, m;
int a[N];
int f[N][M];
int main() {
cin >> n >> m;
f[0][0] = 1;
for (int i = 1; i <= n; i++) {
cin >> a[i];
for (int j = 0; j <= m; j++) {
//不管能不能选,都可以从上一个状态继承过来
f[i][j] = f[i - 1][j];
//如果可选,还要增加另一些状态的方案数
if (j >= a[i]) f[i][j] += f[i - 1][j - a[i]];
}
}
//输出结果
printf("%d", f[n][m]);
return 0;
}
三、一维实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
int n, m;
int a[N];
int f[N];//在前i个物品,体积是j的情况下,恰好装满的方案数
int main() {
cin >> n >> m;
//体积恰好j, f[0]=1, 其余是0
f[0] = 1;
for (int i = 1; i <= n; i++) {
cin >> a[i];
for (int j = m; j >= a[i]; j--)
f[j] += f[j - a[i]];
}
printf("%d", f[m]);
return 0;
}