一、题目解析
物品个数为 \(n\),总体积为\(m\),初步识别是一个 背包问题
观察到每个物品有 数量限制,断定该题是 多重背包问题
本题是一道 多重背包 的裸题
不多废话,我们直接上 闫氏DP分析法
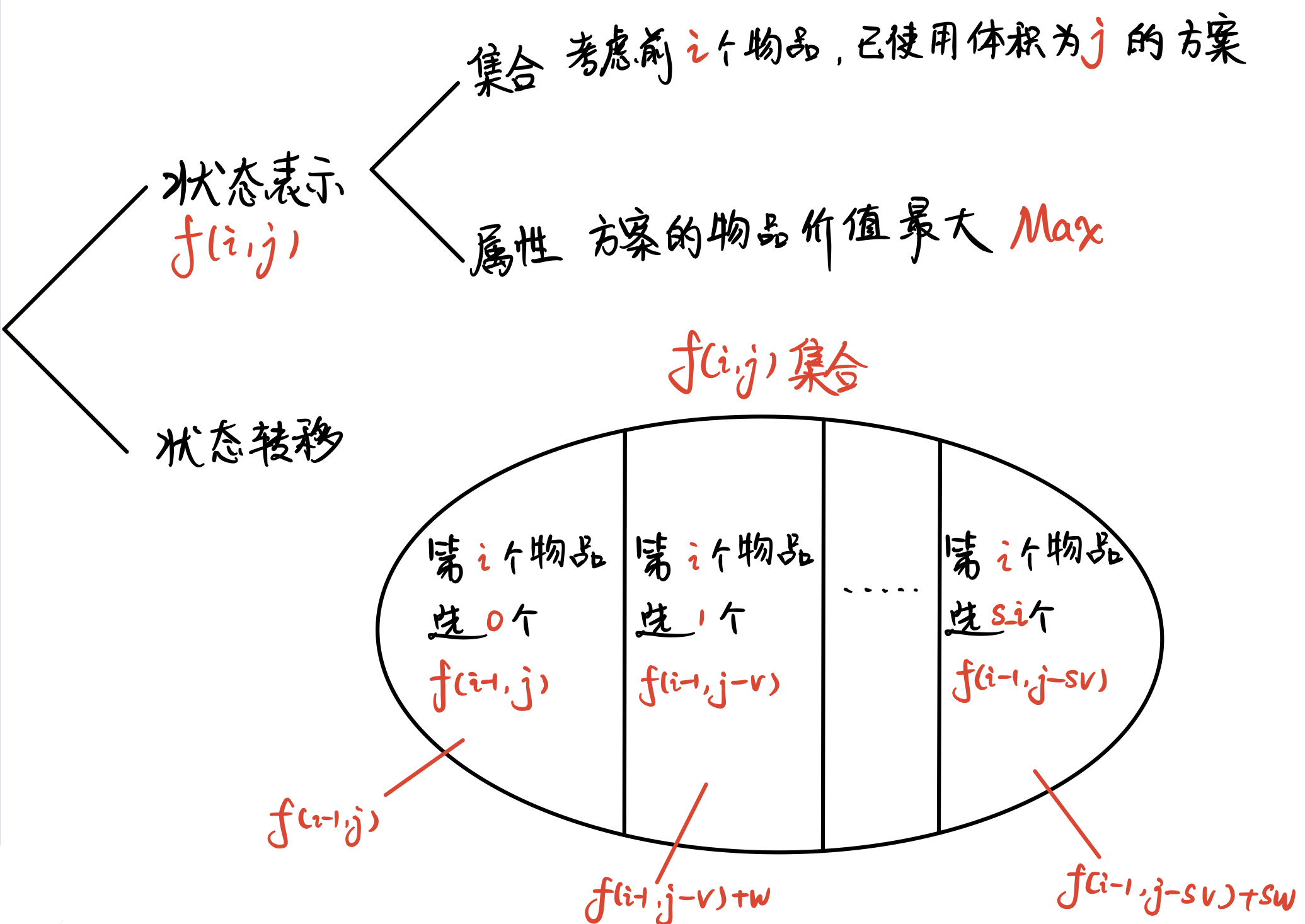
闫氏DP分析法
初始状态:f[0][0]
目标状态:f[n][m]
二、朴素版本解法
#include <bits/stdc++.h>
using namespace std;
const int N = 510, M = 6010;
int n, m;
int v[N], w[N], s[N];
int f[N][M];
//二维朴素作法
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= s[i] && j >= k * v[i]; k++)
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
cout << f[n][m] << endl;
return 0;
}
三、滚动数组模方法优化空间
#include <bits/stdc++.h>
using namespace std;
const int N = 510, M = 6010;
int n, m;
int v[N], w[N], s[N];
int f[2][M];
//二维朴素作法[滚动数组 模]
/*思想:
1、降低空间复杂度
2、每行只依赖上一行,所以可以以2行换多行
3、%2:因为i从1开始,所以就是奇数%2=1,偶数%2=0,交替进行,只保留了上一行和本行,节约空间
*/
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= s[i] && j >= k * v[i]; k++)
f[i % 2][j] = max(f[i % 2][j], f[(i - 1) % 2][j - k * v[i]] + k * w[i]);
cout << f[n % 2][m] << endl;
return 0;
}
四、与1方法优化空间
#include <bits/stdc++.h>
using namespace std;
const int N = 510, M = 6010;
int n, m;
int v[N], w[N], s[N];
int f[2][M];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k <= s[i] && j >= k * v[i]; k++)
f[i & 1][j] = max(f[i & 1][j], f[(i - 1) & 1][j - k * v[i]] + k * w[i]);
cout << f[n & 1][m] << endl;
return 0;
}
五、倒序优化空间
#include <bits/stdc++.h>
using namespace std;
const int N = 510;
const int M = 6010;
int n, m;
int v[N], w[N], s[N];
int f[M];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i++)
for (int j = m; j >= v[i]; j--)
for (int k = 0; k <= s[i] && j >= k * v[i]; k++)
f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
cout << f[m] << endl;
return 0;
}
六、二进制优化速度
#include <bits/stdc++.h>
using namespace std;
const int N = 12010;
int n, m;
int v[N], w[N];
int f[N];
int idx;
//多重背包的二进制优化
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) {
int vi, wi, si;
cin >> vi >> wi >> si;//二进制优化,能打包则打包之,1,2,4,8,16,...
int b = 1;
while (b <= si) {
v[++idx] = vi * b;
w[idx] = wi * b;
si -= b;
b *= 2;
}
//剩下的
if (si > 0) {
v[++idx] = vi * si;
w[idx] = wi * si;
}
}
for (int i = 1; i <= idx; i++)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d", f[m]);
return 0;
}
七、单调队列优化版本
#include <bits/stdc++.h>
using namespace std;
const int N = 1010, M = 20010;
//滚动数组写法
int n, m;
int v[N], w[N], s[N];
int f[2][M];
int q[M];
int main() {
cin >> n >> m;
for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; i++)
for (int r = 0; r < v[i]; r++) {
int hh = 0, tt = -1;//队列中放的是前面s个可能转移过来的剩余空间
for (int j = r; j <= m; j += v[i]) {
//j和q[hh]之间可以装的下的物品个数,一旦大于固定数量,队首出队
while (hh <= tt && j - q[hh] > s[i] * v[i]) hh++;
while (hh <= tt && f[(i - 1) & 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <= f[(i - 1) & 1][j]) tt--;
q[++tt] = j;
f[i & 1][j] = f[(i - 1) & 1][q[hh]] + (j - q[hh]) / v[i] * w[i];
}
}
cout << f[n & 1][m] << endl;
return 0;
}