AcWing 1057. 股票买卖 IV

题目传送门

一、画图分析状态机

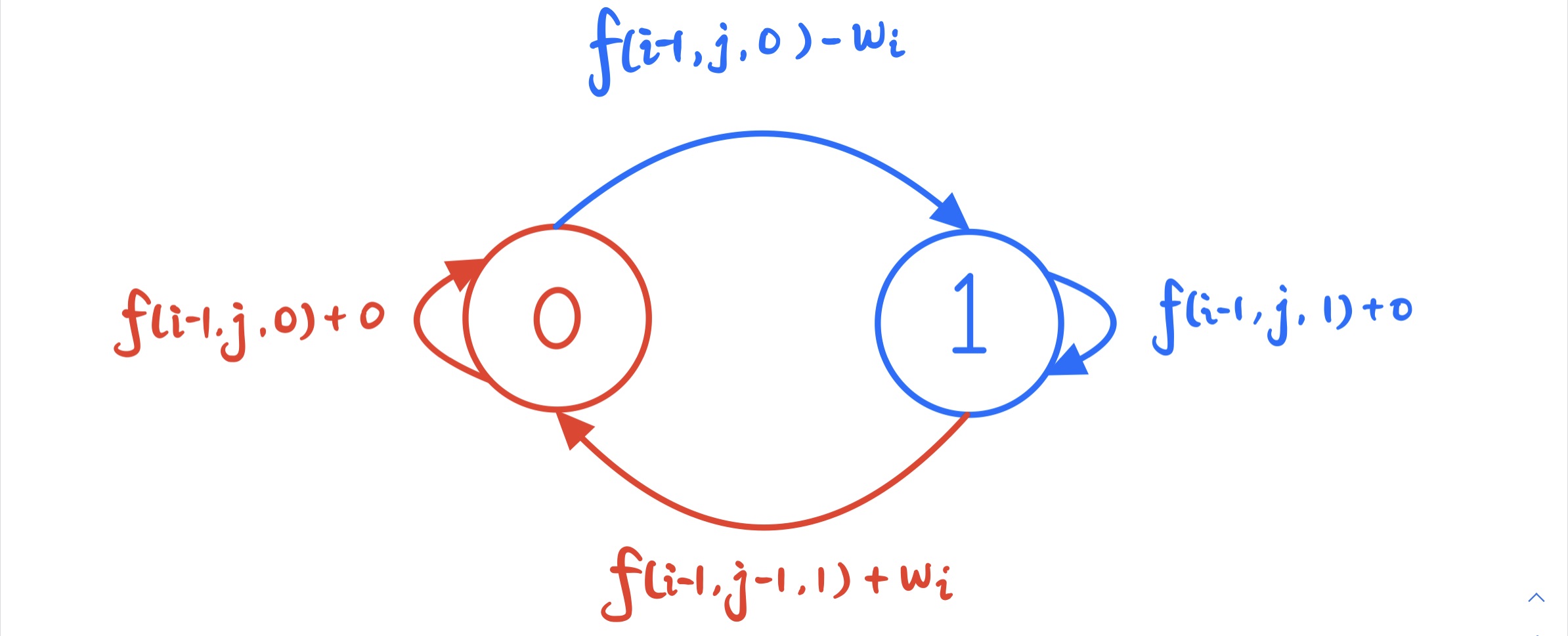
二、状态机分析法

闫式DP分析法--状态机分析法

• 集合
  \(f[i,j,0]\):只考虑前\(i\)天，且已经进行完\(j-1\)次交易，正在进行第\(j\)次交易，且手中无货的所有购买方式的集合。
  \(f[i,j,1]\):只考虑前\(i\)天，且已经进行完\(j-1\)次交易，正在进行第\(j\)次交易，且手中有货的所有购买方式的集合。

• 属性：最大值

• 状态计算
  根据状态机的图来进行分析写出:

\(f[i,j,0]=max(f[i-1,j,0],f[i-1,j,1]+w[i])\)

\(f[i,j,1]=max(f[i-1,j,1],f[i-1,j-1,0]-w[i])\)

【注】：卖出行为 会构成一次完整的交易，所以进行该类转移时， j 的参数也要变动

时间复杂度： \(O(N×K)\)
空间复杂度： \(O(N×K)\)
初始状态: \(f(0,0,0)\)
目标状态: \(f(n,j,0)\)其中\(0≤j≤k\)

三、实现代码[朴素版本]

#include <bits/stdc++.h>

using namespace std;
const int N = 100010;
const int M = 110;
int n;          //n天
int k;          //可以完成的最大交易数量
int w[N];       //每一天的股票价格

int f[N][M][2];

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> w[i];//读入每一天的股票价格

    //不合法状态初始化成-INF(求最大值更新为—INF,求最小值更新成INF)
    memset(f, -0x3f, sizeof f);
    //前i天交易,交易完成次数为0,手中无股票的状态全为0
    for (int i = 0; i <= n; i++) f[i][0][0] = 0;

    //dp
    for (int i = 1; i <= n; i++) //遍历每一天
        for (int j = 1; j <= k; j++) { //遍历每一个可以完成的最大交易数量
            f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + w[i]);
            f[i][j][1] = max(f[i - 1][j][1], f[i - 1][j - 1][0] - w[i]);
        }
    //我们发现买入不卖一定不是最优解,所以不用枚举f[i][j][1]的状态
    int res = 0;
    for (int i = 0; i <= k; i++) res = max(res, f[n][i][0]);
    //输出
    printf("%d\n", res);
    return 0;
}

四、滚动数组优化

#include <bits/stdc++.h>

using namespace std;
const int N = 100010;
const int M = 110;
int n;          //n天
int k;          //可以完成的最大交易数量
int w[N];       //每一天的股票价格

int f[2][M][2];

int main() {
    cin >> n >> k;
    for (int i = 1; i <= n; i++) cin >> w[i];//读入每一天的股票价格

    //不合法状态初始化成-INF(求最大值更新为—INF,求最小值更新成INF)
    memset(f, -0x3f, sizeof f);
    //前i天交易,交易完成次数为0,手中无股票的状态全为0
    for (int i = 0; i <= n; i++) f[i & 1][0][0] = 0;
    //等价于f[1][0][0]=f[0][0][0]=0

    //dp
    for (int i = 1; i <= n; i++) //遍历每一天
        for (int j = 1; j <= k; j++) { //遍历每一个可以完成的最大交易数量
            f[i & 1][j][0] = max(f[i - 1 & 1][j][0], f[i - 1 & 1][j][1] + w[i]);
            f[i & 1][j][1] = max(f[i - 1 & 1][j][1], f[i - 1 & 1][j - 1][0] - w[i]);
        }
    //我们发现买入不卖一定不是最优解,所以不用枚举f[i][j][1]的状态
    int res = 0;
    for (int i = 0; i <= k; i++) res = max(res, f[n & 1][i][0]);
    //输出
    printf("%d\n", res);
    return 0;
}