Acwing 1058 股票买卖V

题目传送门

一、题目描述

给定一个长度为 \(N\) 的数组 \(w\)，数组的第 \(i\) 个元素 \(w_i\) 表示第 \(i\) 天的股票 价格

1. 一次买入一次卖出为一笔 合法交易，且不能同时产生多笔交易（必须在再次购买前出售掉之前的股票）

2. 卖出股票后，无法在第二天买入股票（冷冻期为\(1\)天）

设计一个方案，使得总利润最大

二、分析

以 线性 的方式 动态规划，考虑第 \(i\) 阶段/天 的状态，需要记录的参数有哪些：

第 \(i\) 天的 决策状态：
\((j=0)\) 当前没有股票，且不处于冷冻期 （空仓）
\((j=1)\) 当前有股票 （持仓）
\((j=2)\) 当前没有股票，且处于冷冻期 （冷冻期）

注意：这里的 冷冻期 状态，实际意义是指当天卖出了股票，所以 后一天是没法交易

三、状态机模型分析

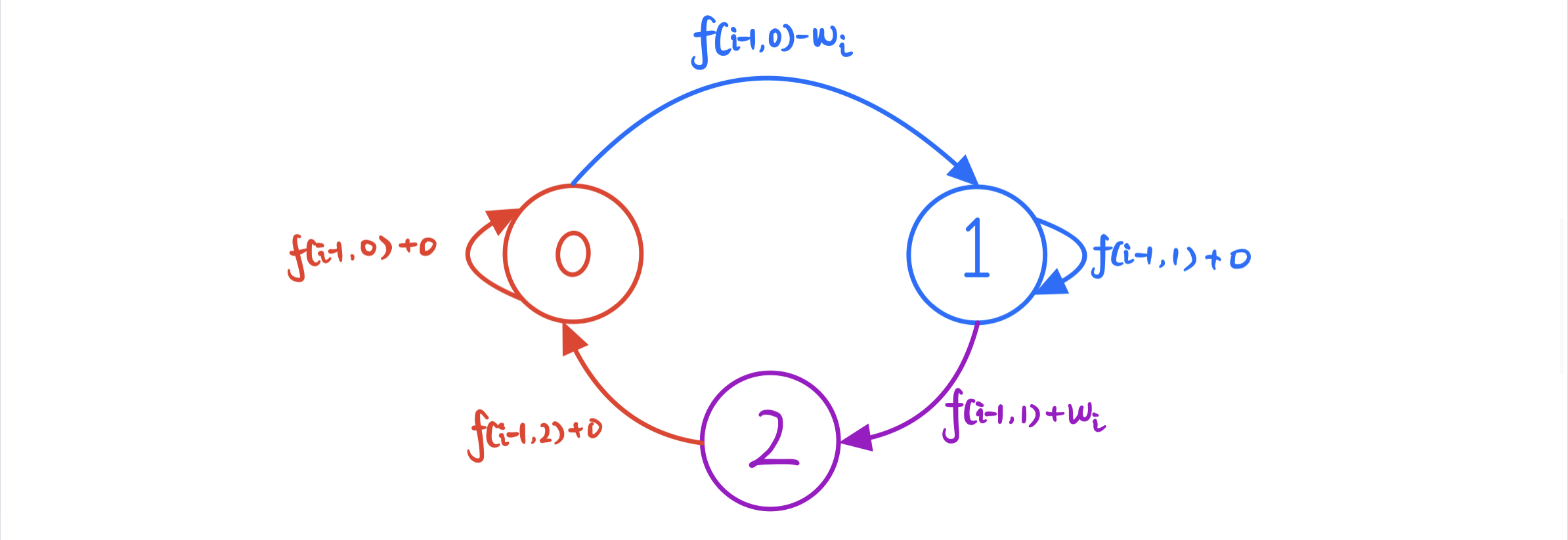
如果第 \(i\) 天是 空仓 (\(j=0\)) 状态，则 \(i-1\) 天可能是 空仓 (\(j=0\)) 或 冷冻期 (\(j=2\)) 的状态

如果第 \(i\) 天是 持仓 (\(j=1\)) 状态，则 \(i-1\) 天可能是 持仓 (\(j=1\)) 状态 或 空仓 (\(j=0\)) 的状态 （买入）

如果第 \(i\) 天是 冷冻期 (\(j=2\)) 状态，则 i-1 天只可能是 持仓 (\(j=1\)) 状态，在第 \(i\) 天选择了 卖出

四、闫氏DP分析法

状态表示\(f[i][j]\)属性: 考虑前 \(i\) 天股市，当前第 \(i\) 天的状态是 \(j\) 的方案

状态表示\(f[i][j]\)集合: 方案的总利润 最大\(Max\)

状态计算\(f[i][j]\)

\[\left\{\begin{array}{l} f[i][0]=max(f[i-1][0],f[i-1][2]) \\ f[i][1]=max(f[i-1][1],f[i-1][0]-w_i) \\ f[i][2]=f[i-1][1]+w_i \end{array}\right. \]

初始状态： \(f[0][0]\) , 其它的状态初始化为\(-INF\),表示其它状态暂不可达,可以结合实例进行思考设计

目标状态： \(f[n][j]\)其中\(j=0,2\)

四、朴素作法

时间复杂度： \(O(N)\)
空间复杂度： \(O(N)\)

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;

int n;
int w[N];
int f[N][3];

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> w[i];
    memset(f, -0x3f, sizeof f);//无法判定或肯定不合理的
    //这个状态是合理的
    f[0][0] = 0;
    for (int i = 1; i <= n; ++i) {
        f[i][0] = max(f[i - 1][0], f[i - 1][2]);
        f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
        f[i][2] = f[i - 1][1] + w[i];
    }
    cout << max(f[n][0], f[n][2]) << endl;
    return 0;
}

五、滚动数组优化

滚动数组优化
时间复杂度： \(O(N)\)
空间复杂度： \(O(1)\)

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;

int n;
int w[N];
int f[2][3];

int main() {
    cin >> n;
    for (int i = 1; i <= n; ++i) cin >> w[i];

    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;
    for (int i = 1; i <= n; ++i) {
        f[i & 1][0] = max(f[(i - 1) & 1][0], f[(i - 1) & 1][2]);
        f[i & 1][1] = max(f[(i - 1) & 1][1], f[(i - 1) & 1][0] - w[i]);
        f[i & 1][2] = f[(i - 1) & 1][1] + w[i];
    }
    cout << max(f[n & 1][0], f[n & 1][2]) << endl;
    return 0;
}