1146 Topological Order (25分)

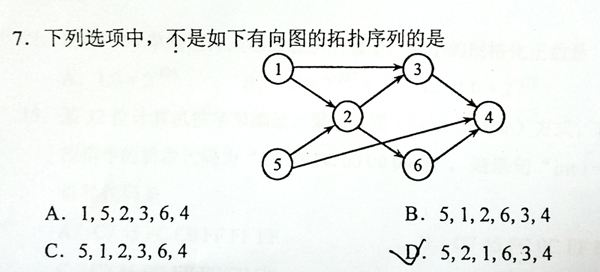
This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

 

Sample Output:

3 4

拓扑排序，已知一个图和若干序列，求序列是否符合拓扑序列。

我们可以进行遍历，将入度++，并且求拓扑序列的时候，只需要判断是否为0，然后将该节点后面节点进行入度--即可。

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
int N, M, K, path[1010][1010] = {0}, a, b, arr[1010], in_degree[1010] = {0};
vector<int> ans;
int main() {
    cin >> N >> M;
    while(M--) {
        cin >> a >> b;
        path[a][b] = 1;
        in_degree[b]++;
    }
    cin >> K;
    for(int c = 0; c < K; c++){
        for(int i = 0; i < N; i++) cin >> arr[i];
        int cp[1010];
        memcpy(cp, in_degree, 1010 * sizeof(int));
        bool add = false;
        for(int i = 0; i < N; i++) {
            if(cp[arr[i]] == 0) {
                for(int j = 1; j <= N; j++) 
                    if(path[arr[i]][j]) cp[j]--;
            } else add = true;
        }
        if(add) ans.push_back(c);
    }
    cout << ans[0];
    for(int i = 1; i < ans.size(); i++)
        cout << " " << ans[i];
    return 0;
}