P1364 医院设置

P1364 医院设置

题目描述

设有一棵二叉树，如图：

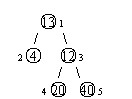
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 11。如上图中，若医院建在1 处，则距离和 =4+12+2 imes20+2 imes40=136=4+12+2×20+2×40=136；若医院建在 33 处，则距离和 =4 imes2+13+20+40=81=4×2+13+20+40=81。

输入格式

第一行一个整数 nn，表示树的结点数。

接下来的 nn 行每行描述了一个结点的状况，包含三个整数 w, u, vw,u,v，其中 ww 为居民人口数，uu 为左链接（为 00 表示无链接），vv 为右链接（为 00 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例

输入 #1复制

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1复制

81

说明/提示

数据规模与约定

[对于 100\% 的数据，保证 1 leq n leq 1001≤n≤100，\0 leq u, v leq n0≤u,v≤n，1 leq w leq 10^51≤w≤105。 ]

这题是一题典型的Floyd算法，我们使用一个全图进行记录最短路径，最后进行遍历，当以i为基站时，各个顶点到它的最短路*权值。

#include <iostream>
#include <algorithm>
#include <cstdio>
#define M 0x7fffffff
using namespace std;
int W[110] = {0}, path[110][110], n, a, b;
int main() {
    fill(path[0], path[0] + 110 * 110, 99999);
    scanf("%d", &n);
    // 存储图
    for(int i = 1; i <= n; i++){
        scanf("%d%d%d", &W[i], &a, &b);
        path[i][i] = 0;
        if(a > 0) path[i][a] = path[a][i] = 1; 
        if(b > 0) path[i][b] = path[b][i] = 1;
    } 
    // 使用Floyd算法求每两点的最短路
    for(int k = 1; k <= n; k++) 
        for(int i = 1; i <= n; i++) 
            for(int j = 1; j <= n; j++) 
                if(path[i][k] + path[k][j] < path[i][j]) 
                    path[i][j] = path[i][k] + path[k][j];
    // 求最小顶点
    int minTotal = M;
    for(int i = 1; i <= n; i++) {
        int total = 0;
        for(int j = 1; j <= n; j++) 
            total += W[j] * path[i][j];
        if(total < minTotal) minTotal = total;
    }
    printf("%d", minTotal);
	return 0;
}