C. Bear and Colors

C. Bear and Colors

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Bear Limak has n colored balls, arranged in one long row. Balls are numbered 1 through n, from left to right. There are n possible colors, also numbered 1 through n. The i-th ball has color t_i.

For a fixed interval (set of consecutive elements) of balls we can define a dominant color. It's a color occurring the biggest number of times in the interval. In case of a tie between some colors, the one with the smallest number (index) is chosen as dominant.

There are 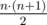non-empty intervals in total. For each color, your task is to count the number of intervals in which this color is dominant.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 5000) — the number of balls.

The second line contains n integers t₁, t₂, ..., t_n (1 ≤ t_i ≤ n) where t_i is the color of the i-th ball.

Output

Print n integers. The i-th of them should be equal to the number of intervals where i is a dominant color.

Examples

Input

4
1 2 1 2

Output

7 3 0 0 

Input

3
1 1 1

Output

6 0 0 

Note

In the first sample, color 2 is dominant in three intervals:

• An interval [2, 2] contains one ball. This ball's color is 2 so it's clearly a dominant color.
• An interval [4, 4] contains one ball, with color 2 again.
• An interval [2, 4] contains two balls of color 2 and one ball of color 1.

There are 7 more intervals and color 1 is dominant in all of them.

 模拟每个区间，通过if(cnt[a[j]]>cnt[a[best]]||(cnt[a[j]] == cnt[a[best]]&&a[j]<a[best]))  best = j来转移

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int maxn = 5005;
int a[maxn],cnt[maxn],ans[maxn];
void solve(){
    int n;
    scanf("%d",&n);
    for(int i = 1; i<=n; i++) scanf("%d",&a[i]);
    for(int i = 1; i<=n; i++){
       // ans[a[i]]++;
        int best = i;
        memset(cnt,0,sizeof(cnt));
      // for(int j = i; j<=n; j++) cnt[a[j]] = 0;
        for(int j = i; j<=n; j++)
        {
            cnt[a[j]]++;
            if(cnt[a[j]]>cnt[a[best]]||(cnt[a[j]] == cnt[a[best]]&&a[j]<a[best]))  best = j;
                ans[a[best]]++;
        }
    }
        for(int i = 1; i<n; i++)
        {
            printf("%d ",ans[i]);
        }
        printf("%d",ans[n]);

}
int main()
{
    solve();
    return 0;
}