D. Directed Roads
ZS the Coder and Chris the Baboon has explored Udayland for quite some time. They realize that it consists of ntowns numbered from 1 to n.
There are n directed roads in the Udayland. i-th of them goes from town i to some other town ai (ai ≠ i). ZS the Coder can flip the direction of any road in Udayland, i.e. if it goes from town A to town B before the flip, it will go from town B to town A after.
ZS the Coder considers the roads in the Udayland confusing, if there is a sequence of distinct towns A1, A2, ..., Ak(k > 1) such that for every 1 ≤ i < k there is a road from town Ai to town Ai + 1 and another road from town Ak to town A1. In other words, the roads are confusing if some of them form a directed cycle of some towns.
Now ZS the Coder wonders how many sets of roads (there are 2n variants) in initial configuration can he choose to flip such that after flipping each road in the set exactly once, the resulting network will not be confusing.
Note that it is allowed that after the flipping there are more than one directed road from some town and possibly some towns with no roads leading out of it, or multiple roads between any pair of cities.
The first line of the input contains single integer n (2 ≤ n ≤ 2·105) — the number of towns in Udayland.
The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ n, ai ≠ i), ai denotes a road going from town i to town ai.
Print a single integer — the number of ways to flip some set of the roads so that the resulting whole set of all roads is not confusing. Since this number may be too large, print the answer modulo 109 + 7.
3
2 3 1
6
4
2 1 1 1
8
5
2 4 2 5 3
28
Consider the first sample case. There are 3 towns and 3 roads. The towns are numbered from 1 to 3 and the roads are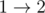 
, 
, 
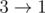initially. Number the roads 1 to 3 in this order.
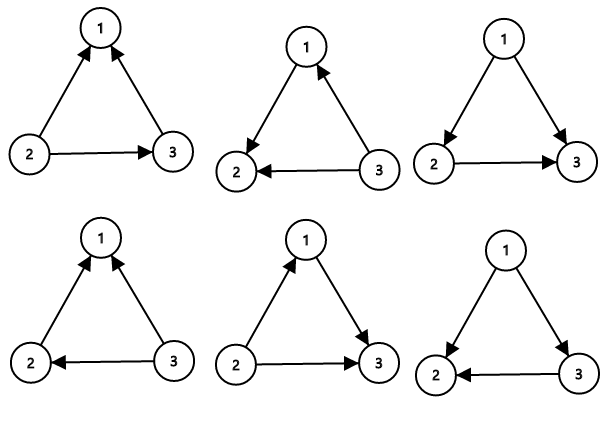
The sets of roads that ZS the Coder can flip (to make them not confusing) are{1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}. Note that the empty set is invalid because if no roads are flipped, then towns1, 2, 3 is form a directed cycle, so it is confusing. Similarly, flipping all roads is confusing too. Thus, there are a total of 6 possible sets ZS the Coder can flip.
The sample image shows all possible ways of orienting the roads from the first sample such that the network is not confusing.
找到所有的环，对于每个环，算出每个环的节点，每一条边都可翻或不翻，有2^n种情况，减去初始情况，和所有边都翻转的情况，2^n-2.
记录所有环上的节点，n-sum是剩余节点，然后乘以2^(n-sum).
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include <cmath> 6 #include <vector> 7 using namespace std; 8 const int maxn = 2e5+5; 9 typedef long long ll; 10 const ll mod = 1e9+7; 11 int g[maxn]; 12 int vis[maxn]; 13 int deep[maxn]; 14 ll quick_pow(ll x,int n) 15 { 16 ll res = 1; 17 while(n){ 18 if(n%2) res = res*x%mod; 19 x = x*x%mod; 20 n /= 2; 21 } 22 return res%mod; 23 } 24 int dfs(int fa,int cur,int tot) 25 { 26 deep[cur] = tot; 27 vis[cur] = fa; 28 if(vis[cur]==vis[g[cur]]&&vis[cur]) 29 return (deep[cur]-deep[g[cur]]+1); 30 if(!vis[g[cur]]) return dfs(fa,g[cur],tot+1); //防止出现环算多了 31 return 0; 32 } 33 int main() 34 { 35 int n; 36 scanf("%d",&n); 37 for(int i=1;i<=n;i++) 38 { 39 scanf("%d",&g[i]); 40 } 41 long long sum = 0; 42 long long ans = 1; 43 int node = 0; 44 for(int i=1;i<=n;i++) 45 { 46 if(!vis[i]) 47 { 48 node = dfs(i,i,0); //计算的环中结点有几个 49 if(node>0) //如果无环，不用算了 50 ans = ans*(quick_pow(2,node)-2)%mod; 51 sum += node; 52 } 53 } 54 ans = ans*quick_pow(2,n-sum)%mod; 55 printf("%I64d ",ans); 56 return 0; 57 }