容斥

1.多重集的组合数

这里问题一般的描述为：

 

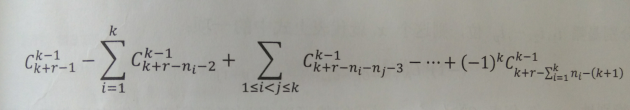
算法竞赛进阶指南上有详细的推导。

例题1： CF 451E Devu and Flowers

直接带公式，但本题 m 太大，先用Lucas对m取模，再转换成排列再乘以逆元就可以了。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll f[30];
const ll mod = 1e9 + 7;
ll inv[30];
///C(y,x)
ll quick_pow(ll a, ll n)
{
    ll res = 1;
    while(n)
    {
        if(n & 1LL) res = res * a % mod;
        n >>= 1LL;
        a = a * a % mod;
    }
    return res;
}
ll C(ll y, ll x)
{
 //   printf("%lld %lld
", y,x);
    if(y < 0 || x < 0 || y < x) return 0;
    y %= mod;
    if(y == 0 || x == 0) return 1;
    ll res = 1;
    for(int i = 0; i < x; i++)
    {
        res = res * (y - i) % mod;
    }
    for(int i = 1; i <= x; i++)
    {
        res = res * inv[i] % mod;
    }
   // printf("%lld
", res);
    return res;
}
int main()
{
    ll n, m;
    cin >> n >> m;
    for(int i = 0; i <= 20; i++)
    {
        inv[i] = quick_pow(i, mod - 2);
       // printf("%lld
", inv[i]);
    }
    for(int i = 1; i <= n; i++) cin >> f[i];
    ll ans = 0;
    for(int x = 0; x < (1 << n); x++)
    {
        if(x == 0)
        {
            ans = (ans + C(n + m - 1, n - 1)) % mod;
        }
        else
        {
            int p = 0;
            ll t = n + m;
            for(int i = 0; i < n; i++)
            {
                if((1 << i) & x)
                {
                    t -= f[i + 1];
                    p++;
                }
            }
            t -= (p + 1);
            if(p & 1)
            {
                ans = (ans - C(t, n - 1) + mod) % mod;
            }
            else
            {
                ans = (ans + C(t, n - 1)) % mod;
            }

        }
      //  cout << ans << endl;
    }
    cout << ans << endl;
    return 0;
}

Code

 2.染色问题

HDU 6314 Matrix

写了一上午公式，用MathType写完截屏过来。

感觉卡的很紧……，把long long都改成了int才过。

#include <bits/stdc++.h>
using namespace std;

const int maxn = 3e3 + 5;
typedef long long ll;
const ll mod = 998244353;
int pw[9000010];
ll qpow(ll a, ll n)
{
    ll res = 1;
    assert(n >= 0);
    while(n)
    {
        if(n & 1) res = res * a % mod;
        a = a * a % mod;
        n >>= 1;
    }
    return res;
}
ll fac[maxn], inv[maxn];
ll pre[maxn][maxn];
int allinv[maxn][maxn];
int main()
{
    pw[0] = inv[0] = fac[0] = 1;
    for(int i = 1; i <= 9000000; i++) pw[i] = pw[i - 1] * 2 % mod;
    for(int i = 1; i <= 3000; i++) fac[i] = fac[i - 1] * i % mod, inv[i] = qpow(fac[i], mod - 2);
    for(int i = 0; i <= 3000; i++)
    {
        for(int j = 0; j <= 3000; j++)
        {
            allinv[i][j] = pw[i * j] * inv[i] % mod * inv[j] % mod % mod;
        }
    }
    for(int s = 0; s <= 3000; s++)
    {
        for(int u = s; u >= 0; u--)
        {
            ll tmp = inv[s - u] * inv[u] % mod;
            if((s - u) & 1) tmp = mod - tmp;
            pre[s][u] = (pre[s][u + 1] + tmp) % mod;
        }
    }
    int n, m, a, b;
    while(scanf("%d %d %d %d", &n, &m, &a, &b) != EOF)
    {
        ll ans = 0;
        for(int p = 0; p < n - a + 1; p++)
        {
            for(int q = 0; q < m - b + 1; q++)
            {
                ans = (ans + pre[n-p][a] * pre[m - q][b] % mod * allinv[p][q]) % mod;
            }
        }
        printf("%lld
", ans * fac[n] % mod * fac[m] % mod);
    }
    return 0;
}

 3.路径问题

The 2018 ACM-ICPC China JiangSu Provincial Programming Contest E. Massage

首先题目要看清楚，JSZKC发两条消息，要求这两条消息走的路径不能有交点，求这种路径的对数。

 这个容斥有点巧妙，从(1,2)到（n-1,m)与(2,1)到(n,m-1)，其中出现的交点 个数= 在从(1,2)到（n,m-1)与(2,1)到(n-1,m)交点个数。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9 + 7;
ll C[2222][2222];
int main()
{
    C[0][0] = C[1][0] = C[1][1] = 1;
    for(int i = 2; i <= 2005; i++)
    {
        C[i][0] = 1;
        for(int j = 1; j <= 2005; j++)
        {
            C[i][j] = (C[i - 1][j] + C[i - 1][j - 1] )% mod;
        }
    }
    //freopen("in.txt", "r", stdin);
   // freopen("out2.txt", "w", stdout);
    int  n, m;
    while(scanf("%d %d", &n, &m) != EOF)
    {
        ll res = C[n + m - 4][n - 2] * C[n + m - 4][n - 2] % mod;
        res = (res + mod - C[n + m - 4][m - 1] * C[n + m - 4][n - 1] % mod) % mod;
        printf("%lld
",res);
    }
    return 0;
}