2020杭电多校

Expectation

 HDU - 6836

对于一张图，每个生成树的权值为所有边按位与的结果，求生成树期望权值。

朴素解法：暴力求出每一个生成树，累积权值和，然后除生成树总数。

int类型只有31位，既然是与的结果，对于每一条生成树所有的边该位都应该是1，

按位枚举每一位，求出该位为1的生成树权值大小，将结果累积到答案里。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e4+500;
const ll mod=998244353;
int A[40][120][120];
ll determinant(int B[120][120],int n){
    ll res=1;
    for(int i=1;i<=n;i++){
        if(!B[i][i]){
            bool flag=false;
            for(int j=i+1;j<=n;j++){
                if(B[j][i]){
                    flag = true;
                    for(int k=i;k<=n;k++){
                        swap(B[i][k],B[j][k]);
                    }
                    res=-res;
                    break;
                }
            }
            if(! flag)
            return 0;
        }
        
        for(int j=i+1;j<=n;j ++){
            while(B[j][i]){
                ll t=B[i][i]/B[j][i];
                for(int k=i;k<=n;k ++){
                    B[i][k]=( B[i][k]-(t*B[j][k])+mod )%mod;
                    swap(B[i][k],B[j][k]);
                }
                res=-res;
            }
        }
        res= ((res*B[i][i])%mod+mod)%mod;
    }
    return res%mod;
}
ll qpow(ll a, ll b,ll m) {   //计算a的b次方
    ll ans = 1;
    ll base = a;
    while (b) {
        if (b & 1) {
            ans *= base;
            ans %= m;
        }

        base *= base;
        base %= m;
        b >>= 1;   //注意是b>>=1 not b>>1
    }
    return ans;
}
ll inv(ll x){
    return qpow(x,mod-2,mod)%mod;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        int n,m;
        scanf("%d %d",&n,&m);
        memset(A,0,sizeof A);
        for(int i=1;i<=m;i++){
            int u,v,w;scanf("%d %d %d",&u,&v,&w);
            for(int j=0;j<=30;j++){
                if(w>>j&1){
                    A[j][u][u]++;
                    A[j][v][v]++;
                    A[j][u][v]--;
                    A[j][v][u]--;

                }
            }
                 A[31][u][u]++;
                    A[31][v][v]++;
                    A[31][u][v]--;
                    A[31][v][u]--;

        }

        ll ans=0;
        ll cnt=determinant(A[31],n-1);
        for(int i=0;i<=30;i++){
            ll cur=determinant(A[i],n-1)*qpow(2,i,mod)%mod;
            ans=(ans+cur)%mod;
        }
        ans=ans*inv(cnt)%mod;
        printf("%lld
",ans);
    }

    // system("pause");
    return 0;
}

A Very Easy Graph Problem

 HDU - 6832 

一张图，每条边权值为2的  i  次方，求

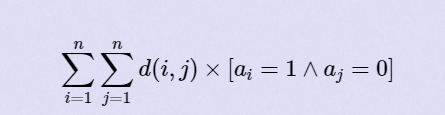
 因为每条边的权值为2的  i  的 次方，那么每两点的最短路即为生成树上的距离，那么直接枚举每一条边，计算它被算多少次即可。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+50;
const ll mod=1e9+7;
int a[N], fa[N],head[N];
int tot0,tot1,ecnt,n,m;
ll ans;
struct edge{
    int v,w,next;
}e[2*N];
void add(int u,int v,int w){
    e[ecnt].v=v;e[ecnt].next=head[u];e[ecnt].w=w;head[u]=ecnt++;
    e[ecnt].v=u;e[ecnt].next=head[v];e[ecnt].w=w;head[v]=ecnt++;
}
int cnt0[N],size[N];
void init(){
    tot0=tot1=ecnt=0;
    ans=0;
    memset(cnt0,0,sizeof cnt0);
    memset(size,0,sizeof size);
    memset(head,-1,sizeof head);
    for(int i=0;i<=n;i++)fa[i]=i;
}
int find(int x){return fa[x]==x?x:fa[x]=find(fa[x]);}
//构建：
void build(int x,int y){int dx=find(x),dy=find(y);if(dx!=dy)fa[dx]=dy;}
ll qpow(ll a, ll b,ll m) {   //计算a的b次方
    ll ans = 1;
    ll base = a;
    while (b) {
        if (b & 1) {
            ans *= base;
            ans %= m;
        }
        base *= base;
        base %= m;
        b >>= 1;   //注意是b>>=1 not b>>1
    }
    return ans;
}

void dfs_size(int u,int fa){
    size[u]=1;
    if(a[u]==0)cnt0[u]=1;
    else cnt0[u]=0;
    for(int i=head[u];~i;i=e[i].next){
        int v=e[i].v;
        if(v==fa)continue;
        dfs_size(v,u);
        size[u]+=size[v];
        cnt0[u]+=cnt0[v];
    }
}
void dfs_ans(int u,int fa){
    for(int i=head[u];~i;i=e[i].next){
        int v=e[i].v;
        if(v==fa)continue;
        ll w=qpow(2,e[i].w,mod);
        ll cur=( (cnt0[v]*(tot1-size[v]+cnt0[v]) )%mod +( (size[v]-cnt0[v])*(tot0-cnt0[v]) )%mod )%mod ;
        cur=(cur*w)%mod;
        ans=(ans+cur)%mod;
        dfs_ans(v,u);
    }

}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d %d",&n,&m);
        init();
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            if(a[i]==0)tot0++;
            else tot1++;
         }
         for(int i=1;i<=m;i++){
            int u,v;
            scanf("%d %d",&u,&v);
            if(find(u)==find(v))continue;
            build(u,v);
            add(u,v,i);
         } 
         dfs_size(1,-1);
         dfs_ans(1,-1);
         printf("%lld
",ans);
    }

    // system("pause");
    return 0;
}