题目大意:
有几座山,如果一座山左右两边的山比它矮,那么可以在这个山上建房子,你有一台挖掘机,每天可以挖一座山一米,问你需要花多少代价可以分别盖1、2、3……座房子。(给出山的数量,以及每座山的高度)。
题目分析:
性质1:不会有两座相邻的山都建房子。性质 2:一座山盖房子就不会被挖,被挖就不会盖房子(两条废话)
每一座山有两种情况:建房子或者不建,可以用一维来保存([ 0 ]/[ 1 ])。
1到第 i 座山的代价和只与 i 前面的两座山有关:如果这座山( i )不建,那么他前面那座山( i-1 )可建可不建,它的代价就是前面山代价的最小值。如果这座山(i)建房,那么它前面的那座山(i - 1)一定不建,它的代价就与前两座山有关系。以此类推,就可以遍历全部求最值。
我们定义一个数组dp[ i ] [ j ] [0/1 ]用来表示前 i 座山中建了 j 个房子的代价 ,最后一维表示当前第 i 座山是否建房子。
如果这座山选择不盖房子,那么它的代价取决于前一座山的情况。

如图:
dp[i][j][0]=min(dp[i-1][j][0],dp[i-1][j][1]+cost(i-1,i));//如果前一座山盖房子,那么这座山有可能挖
cost(i,j)函数表示 i 盖房子需要挖 j 挖多少代价。
int cost(int i,int j){ if(a[j]>=a[i]){ return a[j]-a[i]+1; }else{ return 0; } }
如果这座山盖房子:
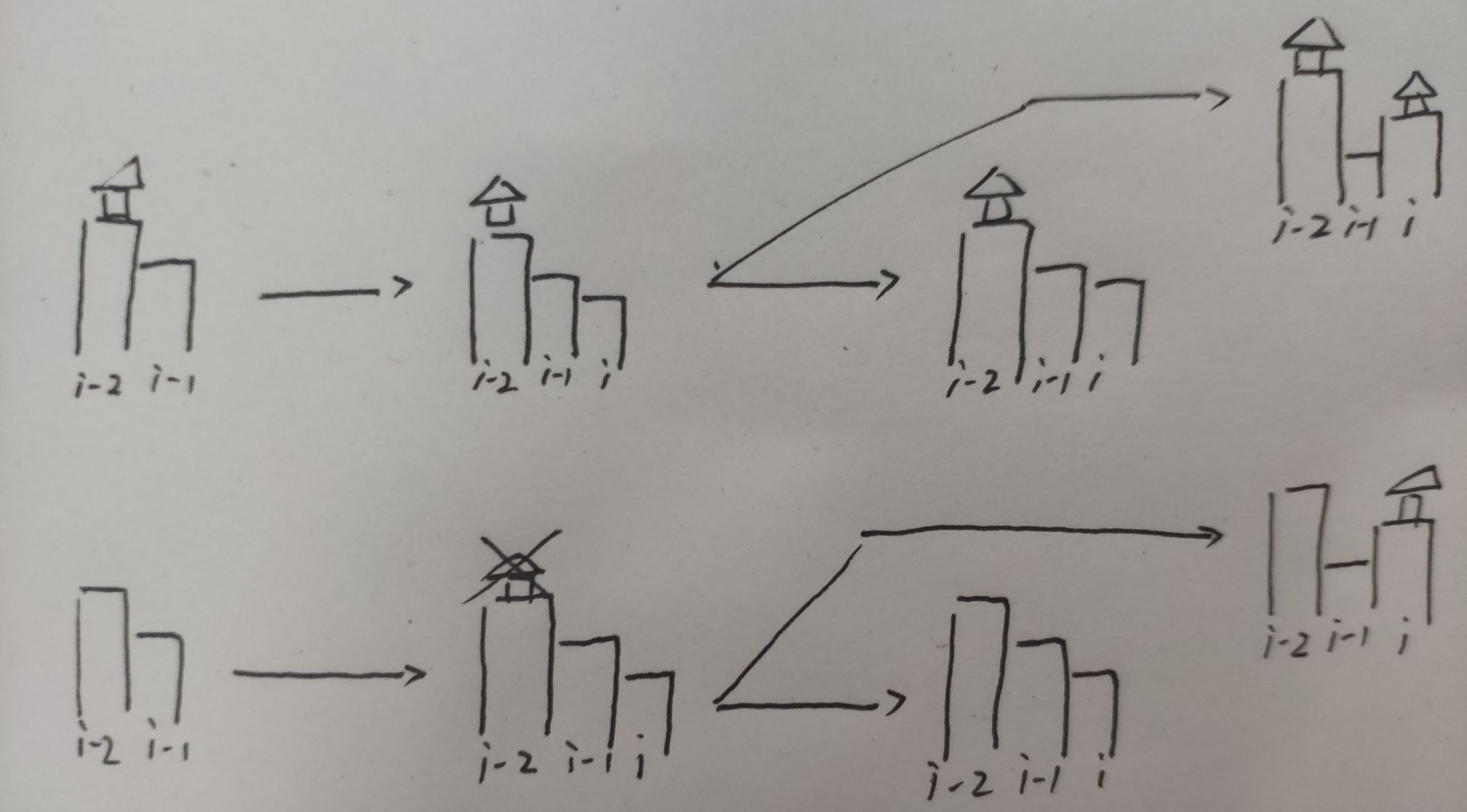
如图,这座山的代价与前面两座山都有关。
如果 i 选择盖房子,那么 i - 1 肯定盖不了,而 i - 2盖不盖房子会产生影响。
如果 i - 2 不盖房子,那就没什么可以担心的,直接挖 i - 1 到比 i 矮就可以了。
如果 i - 2 盖房子,那就要比较到底把 i - 1 挖到比谁矮。
dp[i][j][1]=min(dp[i-2][j-1][0]+cost(i,i-1),dp[i-2][j-1][1]+max(cost(i,i-1),cost(i-2,i-1)));
最后要输出的结果,是盖 1,2,3,……栋房子的最小代价。
首先我们需要知道最多盖几栋房子:
设想:一共n座山,相邻山不能同时盖房子,所以要么盖1、3、5、7……要么盖2、4、6、8……
最多盖( n + 1 )/2栋房子(自己推一下,记住整形运算自动向下取整)
这样结果就出来了,输出相应的 min(dp[ i ][ j ][ 0 ],dp[ i ][ j ][ 1 ])即可。
全代码:
#include<cstdio> #include<iostream> #include<algorithm> #include<cstring> using namespace std; const int maxn=5010; int dp[maxn][maxn][2],a[maxn]; int cost(int i,int j){ if(a[j]>=a[i]){ return a[j]-a[i]+1; }else{ return 0; } } int n,cnt; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ a[i]=0; for(int j=1;j<=n;j++){ dp[i][j][0]=dp[i][j][1]=0x3fffffff; } } for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } dp[1][1][1]=0; dp[2][1][1]=cost(2,1); dp[2][1][0]=cost(1,2); for(int i=3;i<=n;i++){ for(int j=1;j<=i;j++){ dp[i][j][0]=min(dp[i-1][j][0],dp[i-1][j][1]+cost(i-1,i)); dp[i][j][1]=min(dp[i-2][j-1][0]+cost(i,i-1),dp[i-2][j-1][1]+max(cost(i,i-1),cost(i-2,i-1))); if(2*j>=i)break; } } int cnt=(n+1)/2; for(int j=1;j<=cnt;j++){ printf("%d ",min(dp[n][j][1],dp[n][j][0])); } printf(" "); }