(集训模拟赛2)抢掠计划(tarjan强)
题目:给你n个点,m条边的图,每个点有点权,有一些点是“酒吧”点,终点只能在“酒吧”,起点给定,路可以重复经过,但点权只能加一次,求最大的结果。
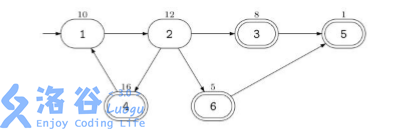
例如这个图,双实线表示是酒吧,结果呢是1->2->4->1->2->3->5所得值。
输入格式:
第一行N,M,下面M行是边,下面N行是点权,下面1行是起点与酒吧数量,下面一行是“酒吧”点的编号。
思路:
注意到:(边可以重复走,而点权只算一遍)这个条件,说明只要走到了一个环中的一个点,这个环里面所有点就一定都能走到,因为你可以走一圈回到入环的起点。
这是什么呢?这是名为“缩点”的高级技巧在呼唤!
我们可以把所有环看作一个点,权值是环内所有点权之和,只要环中有一个点是“酒吧”,那这个大环就可以看作一个“酒吧”,然后从起点所在“大点”开始,跑一遍单源最短路,找最大的路径长度即可(spfa最长路,dfs硬搜会被卡(搜,就硬搜))
代码:

#include<queue> #include<cstdio> #include<iostream> #include<cstring> #include<algorithm> using namespace std; const int maxn=5e5+10; struct E{int from,to,next;}edge[maxn]; E edge2[maxn];int head2[maxn],tot2; int head[maxn],tot; void add(int from,int to){ edge[++tot].from=from; edge[tot].to=to; edge[tot].next=head[from]; head[from]=tot; } void add2(int from,int to){ edge2[++tot2].to=to; edge2[tot2].next=head2[from]; head2[from]=tot2; } int dfn[maxn],vis[maxn],low[maxn]; int sta[maxn],top,Time; int belong[maxn],belongcnt,size[maxn]; int val[maxn],drink[maxn],drink2[maxn]; void tarjan(int u){ if(dfn[u])return; low[u]=dfn[u]=++Time; vis[u]=1;sta[++top]=u; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(!dfn[v]){ tarjan(v); low[u]=min(low[u],low[v]); }else if(vis[v]){ low[u]=min(low[u],dfn[v]); } } if(low[u]==dfn[u]){ belongcnt++; while(sta[top+1]!=u){ belong[sta[top]]=belongcnt; size[belongcnt]+=val[sta[top]]; vis[sta[top]]=0; if(drink[sta[top]])drink2[belong[sta[top]]]=true; top--; } } } int viss[maxn],diss[maxn]; void spfa(int s){ queue<int> q; viss[s]=1;diss[s]=size[s]; q.push(s); while(!q.empty()){ int u=q.front();q.pop();viss[u]=0; for(int i=head2[u];i;i=edge2[i].next){ int v=edge2[i].to; if(diss[v]<diss[u]+size[v]){ diss[v]=diss[u]+size[v]; if(!viss[v]){ viss[v]=1; q.push(v); } } } } } int main(){ int m,n; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ int from,to; scanf("%d%d",&from,&to); add(from,to); } for(int i=1;i<=n;i++){ scanf("%d",&val[i]); } int begin,dnum; scanf("%d%d",&begin,&dnum); for(int i=1;i<=dnum;i++){ int x; scanf("%d",&x); drink[x]=true; } for(int i=1;i<=n;i++){ tarjan(i); } for(int i=1;i<=m;i++){ if(belong[edge[i].from]!=belong[edge[i].to]){ add2(belong[edge[i].from],belong[edge[i].to]); } } //缩完后点之间的边 spfa(belong[begin]); int ans=0; for(int i=1;i<=belongcnt;i++){ if(drink2[i])ans=max(ans,diss[i]);//只有是酒吧才算最大值 } printf("%d",ans); return 0; }
(集训模拟赛3)清理牛棚(思维最短路)
题目:

简而言之,就是给你i个牛,每个牛可以清扫M到E,代价为S,问覆盖全部区间的最小代价(这不显然是线段树板子吗)
分析:
我们可以这么想,如果一头牛从i打扫到j,那么就从i到j+1建一条边(题目中说了牛打扫的是闭区间,所以我们建边时候要处理一下,把[i,j]变成[i,j+1)否则加边区间会重复)
然后呢,我们对于每一个i点,都建一条权值为0的i到i-1的边,然后从起点到终点跑最短路。
这是为什么呢?
我们想一想,如果有两头牛,他们分别打扫1->5,2->6,如果不建反向的权值为0的边,那么这个情况下1和6是不联通的,我们需要解决这种有重叠区间的问题的话,只要从5到2建一条权值为0的边,这样在跑最短路跑到5的时候,可以回到2继续跑。所以,我们的方案就是通过反向建0的边,使本来不联通的“重叠”区间也可以连起来,而且这样不会影响最后结果,之前不联通,这样操作还是不联通,因为反向建的边是单向的,只能从较后位置到较前位置。
代码:

#include<bits/stdc++.h> using namespace std; const int maxn=1e6+10; struct E{ int to,val,next; }edge[maxn]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } int n,m,e; int vis[maxn],d[maxn]; void spfa(int s){ memset(d,0x3f,sizeof(d)); queue<int> q; d[s]=0;vis[s]=1;q.push(s); while(!q.empty()){ int u=q.front(); q.pop(); vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(vis[v])continue; if(d[v]>d[u]+edge[i].val){ d[v]=d[u]+edge[i].val; q.push(v); vis[v]=1; } } } } int main(){ scanf("%d%d%d",&n,&m,&e); for(int i=m;i<=e;i++){ add(i+1,i,0); } for(int i=1;i<=n;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); to++; add(from,to,val); } spfa(m); if(d[e+1]==0x3f3f3f3f){ printf("-1"); return 0; } printf("%d",d[e+1]);//注意最后的区间变成了[m,e+1)而不是[m,e]了 return 0; }
(集训模拟赛4)浇水(思维最短路)
题目:
其实这道题是个贪心
分析:
我们可以这样考虑:每一个喷射装置覆盖一个圆形的面积,但是如果喷射半径小于m/2,那这个喷头相当于废了,它连自己的上下都喷不到,就不可能选它了,接着,面积什么的显然不好处理,还会有一些重叠就更不好了,我们可以把每个喷头所覆盖的n上面长度作为该喷头的“有效范围”,由于上下对称性,只要长方形的一条长被覆盖满了,另外一条必覆盖满,所以我们把这道题看作有n个喷头,每个喷头覆盖l到r,求覆盖所有区间的最小数量。
emm,这句话怎么这么熟悉?看了一下上一道题的描述(显然这两道题是一道题)
所以打出代码来,也跟上一道题是一样的,我就不放代码了
显然还是有一些区别的,比如这道题每一个喷头覆盖区间的左右端点是doube类型,不能直接当结点,会有蛋疼的精度问题,所以……
我们直接把每一个double值扩大一个倍数转成整形,相应的n也扩大,这样就可以代入上一道题的代码了。(×5就可以)
附上代码:

#include<bits/stdc++.h> using namespace std; const int maxn=1e7+10; int k,n,m; struct E{ int to,val,next; }edge[maxn]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } int vis[maxn],d[maxn]; void spfa(int s){ memset(d,0x3f,sizeof(d)); queue<int> q; d[s]=0;vis[s]=1;q.push(s); while(!q.empty()){ int u=q.front(); //printf("%d ",u); q.pop(); vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(vis[v])continue; if(d[v]>d[u]+edge[i].val){ d[v]=d[u]+edge[i].val; q.push(v); vis[v]=1; } } } } int main(){ scanf("%d%d%d",&k,&n,&m); for(int i=1;i<=k;i++){ int aa,r; scanf("%d%d",&aa,&r); if(r<=m/2)continue; int ll=(int)(aa*5-sqrt(r*r-m*m/4)*5); int rr=(int)(aa*5+sqrt(r*r-m*m/4)*5); //区间变为:[当前位置×5-向左的距离×5,当前位置×5+向右的距离×5+1); //因为该区间相当于这个喷头覆盖范围的一个弦,所以左右延伸的距离(半弦长)=根号(半径平方-弦心距平方)/2; if(ll<0)ll=0; add(ll,rr+1,1); } for(int i=1;i<=n*25;i++)add(i,i-1,0); spfa(0); if(d[n*5+1]==0x3f3f3f3f)d[n*5+1]=-1; printf("%d",d[n*5+1]); return 0; }
(集训模拟赛8)升降梯上(思维最短路)
(集训模拟赛8)升降梯上(分层图最短路)
题目大意:
有n层楼,你现在在第1层,有一个电梯,上面有个拉杆,有m个控制槽,槽上有数字,拨到哪个槽就上升相应层数(不能下降到<=0或上升到>n层),最开始拉杆在“0”槽位处,数字有正有负,且控制槽之间的数字是有顺序的,每移动一格控制槽需要1s,每上或下一层楼要2s,问走到顶楼的最小时间。
分析:(看起来是个dp,好像也可以推出来转移方程,但是会有一些小问题,这边只考虑正解(最短路)。)
我们把每种需要花费时间的操作当成边来处理,时间就是边的权值。
我们可以把每一层的每一个控制槽看作一个结点,它向本层的其它槽位的点建边(因为这需要话费时间),还向它指向的那一层的这个槽建一条边(同上),权值按照题目要求设定。(注意:二维的点(i,j)不适合作为图的结点,我们可以把每一个点的坐标处理一下,变成一维的点,然后剩下的操作就好处理了。)
主要步骤:
1.转点,第一层的点从1到m,第二层的点是m+1到2*m……第n层的点是(n-1)*m+1到n*m。
2.建边,每一个点向周围的槽位和自己指向的槽位建边。
3.最短路,需要从第一层的“0”槽到顶层的槽位中找最小值。
附上代码:

#include<bits/stdc++.h> using namespace std; const int maxn=1e6+10; struct E{ int from; int to,val,next; }edge[maxn]; int head[maxn],tot,dis[maxn],vis[maxn]; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].from=from; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } void spfa(int s){ memset(dis,0x3f,sizeof(dis));memset(vis,0,sizeof(vis)); dis[s]=0;vis[s]=1; queue<int> q; q.push(s); while(!q.empty()){ int u=q.front();q.pop();vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(dis[v]>dis[u]+edge[i].val){ dis[v]=dis[u]+edge[i].val; if(!vis[v]){ q.push(v);vis[v]=1; } } } } } int n,m,c[maxn]; int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;i++)scanf("%d",&c[i]);//每一个槽位及上面的数字 //建同一层之间的边 for(int now=1;now<=n;now++){ for(int i=1;i<=m;i++){ for(int d=0;d<=m-1;d++){ if(i+d<=m)add((now-1)*m+i,(now-1)*m+i+d,d); if(i-d>=1)add((now-1)*m+i,(now-1)*m+i-d,d); } } } //建层与层之间的边 for(int now=1;now<=n;now++){ for(int i=1;i<=m;i++){ if((now-1+c[i])*m+i<=n*m&&(now-1+c[i])*m+i>=1){//边界条件:不超过最大节点(n*m)不小于最小节点(1) if(c[i]==0)continue; add((now-1)*m+i,(now-1+c[i])*m+i,2*abs(c[i])); } } } int start=0; for(int i=1;i<=m;i++){ if(c[i]==0)start=i; } spfa(start); int Min=0x7fffffff; for(int i=1;i<=m;i++){ Min=min(Min,dis[(n-1)*m+i]); } if(Min==0x3f3f3f3f)Min=-1; printf("%d",Min); return 0; }
(集训模拟赛9)最小环(思维最短路)
题目:
思路:
这道题要求求已知起点的一条最小环,边是无向的但每条边又只能走一次(一看到最小环不就应该知道是最短路了吗)
一般求最小环都是用floyd算法,详情请见老姚博客:https://www.cnblogs.com/hbhszxyb/p/12770720.html
这道题显然n3的效率会炸,所以我们需要另寻它法。
我们知道,一个简单环,断掉一条边就会形成一条链,我们可以利用这一点,尝试断掉某个点与起点相连的一条边,再求起点到它的最短路,那么到这个点的最短路+断掉的这条边权就是起点与这个点所在的环的大小了,我们枚举每一条与起点相连的边,并尝试断掉它,然后求环的大小,取最小值即可。
注意:每次断边要断两个,建议在建边时候按^1的方法去建(0、1是一对反向边,2、3是一对反向边,4、5是一对……),这样在断边时候好处理
附上代码:

#include<bits/stdc++.h> using namespace std; const int maxn=4e5+10; struct E{int to,next,val;}edge[maxn]; int head[maxn],tot,Min=0x3f3f3f3f; void add(int from,int to,int val){ edge[tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot++; } int d[maxn],vis[maxn]; void spfa(int s){ memset(d,0x3f,sizeof(d)); memset(vis,0,sizeof(vis)); queue<int> q; d[s]=0; q.push(s); while(!q.empty()){ int u=q.front();q.pop();vis[u]=0; for(int i=head[u];~i;i=edge[i].next){ int v=edge[i].to; if(d[v]>d[u]+edge[i].val){ d[v]=d[u]+edge[i].val; if(!vis[v]){ q.push(v); vis[v]=1; } } } } } int n,m,t,from,to,val; int main(){ scanf("%d",&t); while(t--){ memset(head,-1,sizeof(head));tot=0; scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ scanf("%d%d%d",&from,&to,&val); add(from,to,val); add(to,from,val); } Min=0x3f3f3f3f; for(int i=head[1];~i;i=edge[i].next){ int now=edge[i].val;//断掉这条边的边权 int v=edge[i].to;//某个与起点直接相连的点 edge[i].val=edge[i^1].val=0x3f3f3f3f;//断边(给它恢复初始值) spfa(1); Min=min(Min,d[v]+now); edge[i].val=edge[i^1].val=now;//再建回来 } if(Min==0x3f3f3f3f)Min=-1; printf("%d ",Min); } return 0; }
(集训模拟赛10)虫洞(分层图最短路)
题目描述
输入格式
思路:
这道题乍一看是一个最短路,但是它有一些特殊限制,我们就考虑分层图。
何谓分层图?
就是在同一个图里面不太好找出所有情况时,开几个一样的图,在图之间进行那些“特殊操作”(例如边权改为0,边权减半,反向走……),这样不打破原来图的结构,还能更方便快捷的求出结果。
这道题,我们就可以把双数时间点的图和单数时间点的图分开来,建成两个图,因为单数时间和双数时间的黑、白洞情况不同,其他的差别也只在这两个图之间发生。
这道题有几个难处理的地方:
1、一个洞跳到另一个洞后,所有洞的颜色都会改变,我们可以通过再两个图之间建边这个问题,例如样例:
1 2 3 4(洞编号)(黑洞为1,白洞为0)
1 0 1 0(偶数时间状态)
0 1 0 1(奇数时间状态)
我们假如要在3->4这一方向建边,我们就可以让上面图的3号指向下面图的4号,下面图的3号指向上面图的4号,因为从3号到4号转移过后,4号的状态会改变,我们要以4号的新状态再进行之后的操作,所以直接从3号建一条边到改变后的4号,接下来就从改变后的4号再向后进行操作即可。
2.同一个洞可以选择停留,还会消耗1个时间,我们可以在两个图相对应的两个点之间建边解决这个问题。如上图中的1号与下图中的1号,他们之间就满足状态改变,位置不变。
主要思路就是这些,下面附上代码

#include<bits/stdc++.h> using namespace std; const int maxn=100010; int n,m,w[maxn],now[maxn],s; struct E{int to,next,val;}edge[maxn*6]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } int dis[maxn],vis[maxn]; void spfa(int s){ memset(dis,0x3f,sizeof(dis)); queue<int> q; dis[s]=0;q.push(s); while(!q.empty()){ int u=q.front();q.pop();vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(dis[v]>dis[u]+edge[i].val){ dis[v]=dis[u]+edge[i].val; if(!vis[v]){ q.push(v); vis[v]=1; } } } } } void init(){ scanf("%d%d",&n,&m); for(int i=1;i<=n;i++){ scanf("%d",&now[i]); } for(int i=1;i<=n;i++){ scanf("%d",&w[i]); } for(int i=1;i<=n;i++){ scanf("%d",&s); if(now[i]){//如果是黑洞,那么由黑到白要花费s[i]。(这里now[i]表示偶数时间内的状态) add(i,i+n,s); add(i+n,i,0); }else{//如果是白洞,那么由白到黑花费为0。(这两种情况都要建双向边,当边反过来,黑到白也变成了白到黑) add(i,i+n,0); add(i+n,i,s); } } for(int i=1;i<=m;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); if(now[from]==now[to]){ add(from,to+n,val); add(from+n,to,val); //两洞无论什么时候状态都一样,就不用考虑题目中delta的问题 }else{ if(now[from]==1&&now[to]==0){ add(from,to+n,val+abs(w[from]-w[to])); int x=max(0,val-abs(w[from]-w[to])); add(from+n,to,x); //前黑后白 }else if(now[from]==0&&now[to]==1){ add(from+n,to,val+abs(w[from]-w[to])); int x=max(0,val-abs(w[from]-w[to])); add(from,to+n,x); //前白后黑 } } } } int main(){ init(); spfa(1); printf("%d",min(dis[n],dis[2*n]));//两个n结点选最小值 return 0; }
(集训模拟赛12)道路和航线(奇怪的最短路)(洛谷P3008)
这道题显然就是一个最短路,但是这个最短路还不能乱跑:
题目中数据范围边数50000,显然nlogn是可以跑过,但是这道题有负权边,没办法直接跑Dij,怎么办呢(不要跟我说SPFA,它已经死了)
所以这道题我们要通过一些奇奇怪怪的方法,让他能跑Dij。(就是缩点+拓扑排序啦)
分析:
根据题目条件,我们知道道路是双向的且没有负权,航线是单向的但不存在于环中(没有一条航线可以通过其他道路或航线回来)。
我们可以对于每一堆双向的道路们,把它们缩在一起成为一个“联通块”,这样我们就可以在联通块内部跑Dij了,因为没有负权。
对于联通块之间的边,它们只能是航线,而且满足联通块之间没有环,那么:
我们可以通过跑拓扑序的方式来遍历每一个联通块。
正确性?
对于Dij来说,最开始除了起点,其它点的距离都被我们认为是无穷大,那么除了包含起点的联通块,其他联通块里所有点的值都是无穷大,对于这些块与起点块的关系有下面几种:
1.该联通块有一条航线指向起点块,那么由于航线的性质,该联通块内的点相对于起点来说肯定是“不可到达”的,那先遍历它也没什么问题。
2.该联通块被起点块指向,那么这个联通块内至少有一个点会被起点块中的点更新,那么它一定要排在起点块后遍历才能做到更新其内点的值不是无穷大。
3.类似上面的情况,只有所有指向一个块的块们都遍历过了,才会把这个块上该更新的点都更新过了,而且这样跑完之后,一定不会再有别的航线更新这个块了,这么遍历不就是拓扑序遍历吗!(先找入度为0的块,每遍历一条航线,那这条航线指向的块入度--,如果入度为0了,再遍历这个点)
拓扑序部分:

for(int i=1;i<=p;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); add(from,to,val); indegree[belong[to]]++; //这是在读入每一条航线的时候就处理入度了,belong[to]表示to所在的联通块 } for(int i=1;i<=belongcnt;i++){ if(indegree[i]==0)qq.push(i); }//qq是储存入度为0的联通块的队列 while(!qq.empty()){ int x=qq.front();qq.pop(); Dij(x); } //在Dij里面我们会处理减入度的情况 void Dij(){ if(belong[to]!=x){ indegree[belong[to]]--; if(indegree[belong[v]]==0)qq.push(belong[v]); } }
附上全部代码:

#include<bits/stdc++.h> using namespace std; const int maxn=1e6+10; int n,m,p,s; int belong[maxn],belongcnt; vector<int> be[maxn];//这个向量里面保存的是某个联通块里面的所有点 struct E{ int from,to,val,next; }edge[maxn]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].from=from; edge[tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } void dfs(int u){ belong[u]=belongcnt; be[belongcnt].push_back(u); for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(!belong[v])dfs(v); } } int indegree[maxn]; queue<int> qq; struct Node{ int num,dis; Node(){} Node(int x,int y){ num=x,dis=y; } bool operator <(const Node &aa)const{ return dis>aa.dis; } }; priority_queue<Node> q; int dis[maxn]; void Dij(int x){ int size=be[x].size(); for(int i=0;i<size;i++){ int now=be[x][i]; //先把联通块中的所有点放入 q.push(Node(now,dis[now])); } while(!q.empty()){ Node ding=q.top();q.pop(); int u=ding.num,V=ding.dis; if(dis[u]!=V)continue;//这个点的dis值已经被别的更新过了,才会造成这俩不一样 for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(belong[v]!=x){//这个点不属于当前的联通块,肯定是航线 indegree[belong[v]]--; if(indegree[belong[v]]==0)qq.push(belong[v]); //这条航线指向的联通块入度-- } if(dis[u]<0x3f3f3f3f&&dis[v]>dis[u]+edge[i].val){ dis[v]=dis[u]+edge[i].val; if(belong[v]==x)q.push(Node(v,dis[v])); //先把这个联通块的点都跑完,只入队这个联通块里面的点 } //如果u的dis值还是无穷大呢,那就不用更新v了(小小的优化) } } } int main(){ memset(dis,0x3f,sizeof(dis)); scanf("%d%d%d%d",&n,&m,&p,&s); dis[s]=0; for(int i=1;i<=m;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); add(from,to,val);add(to,from,val); } for(int i=1;i<=n;i++){ if(!belong[i]){ belongcnt++; dfs(i); } }//在没读入航线之前,所有的道路们各自为战,不相联通,直接dfs就可求出联通块 for(int i=1;i<=p;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); add(from,to,val); indegree[belong[to]]++; } for(int i=1;i<=belongcnt;i++){ if(indegree[i]==0)qq.push(i); } while(!qq.empty()){ int x=qq.front();qq.pop(); Dij(x); } for(int i=1;i<=n;i++){ if(dis[i]==0x3f3f3f3f)printf("NO PATH "); else printf("%d ",dis[i]); } return 0; }
(dark假期集训%拟赛1)假面舞会(思维图论)(洛谷P1477)
题目:


思路:
这道题目的描述比较复杂,但是实际上我们可以把其中的情况分为以下几种:
1.只有环:
如果几个人构成了一个环,那么这个环上的结点个数的因数就是可能的面具总数。(如果一个环上每个人戴不同面具,那么面具总数就是人数,类似的,我们可以把这个环的人们分成几部分,每一部分人数相等且人人相连,这每一部分的人数也可能是面具的数量,整个环只是这几个面具的循环而已)
例如:
1->2->3->4->5->6->1
可能每个人面具都不同,也可能123面具各不相同,456分别与1、2、3面具相同。
如果这个图里有多个环,那么面具数量最大值就是这些环结点数的最大公约数,最小值就这个数大于等于3的最小因数。
2.只有链:
因为一个链首尾不相连,我们可以认为这个链上任何一个点的面具都不相同,那么面具数量最大值就是链上的结点数。
如果有多个互不相交的链,那么完全可以认为所有人的面具都不一样,最大面具数量就是人数。如果相交,那么一个链集合的最大面具数是其中最长的那条链的长度(原因请看4.中的判链部分)。
我们也可以把链上的所有人看作三个面具(题目所给最小值)的不断循环,而且无论链多长,有几个链,都是可以满足的。
1->2->3->4->5 6->7
如图,面具最大值是7,最小值是3 (1->2->3->1->2 1->2)
3.有环有链:
我们知道,有环的话,那么就会出现面具数量的限制(环的结点数是面具最大值,>=3的最小因数是最小值)
而单独的链是不会出现此类限制,最大的要多少有多少,最小的直接就是3,那么我们可以这样认为:环的限制比链的限制范围要小。(环造成的限制链都能满足,链造成的限制环不一定能满足)那么我们就可以知道在环链同时存在的时候,我们只需要处理环就可以了。
4.不成立的情况
我们根据题目中所描述,可以知道:当多个人能看到同一个人的时候,这“多个人”面具编号一定一样,一个人能看到多个人的时候,这“多个人”面具编号也一样。只有在同一个人看到的“多个人”编号不同或看到同一个人的“多个人”编号不同时,属于“不成立”的情况,要输出“-1 -1”。
我们通过正向建边权值为1,反向建边权值-1的方法来处理这种情况,我们对每个点维护他的深度。
我们可以这么考虑,对于一个点,他指向的(也就是这个人能看到的人们)点的dep值是这个点+1,指向他的(也就是看到这个人的人们)的dep值是这个点-1,这样就能保证刚才所说的条件了,我们可以在判环判链的过程中顺便处理这个问题。
1.判环过程中:通过对每一个我们构建的“联通区域”进行dfs,我们可以得到一些环,在这个过程中,我们如果访问了一个之前访问过的点,那么我们就找到了一个环,我们就把它加到我们的求gcd的数里面,对于不成立的情况,他们的环的大小就会是3以下,在后期的处理中我们可以判掉。

void dfs_huan(int u){ vis[u]=1; for(int i=head[u];~i;i=edge[i].next){ int v=edge[i].to; if(!vis[v]){ dis[v]=dis[u]+edge[i].val; dfs_huan(v); }else{ ans=gcd(ans,abs(dis[u]-dis[v]+edge[i].val)); } } } int main(){ for(int i=1;i<=n;i++){ if(!vis[i]){ dfs_huan(i); } } if(ans!=0){ if(ans<3){ printf("-1 -1 "); return 0; }else{ int i; for(i=3;i<=ans;i++){ if(ans%i==0){ break; } } printf("%d %d ",ans,i); return 0; } } return 0; }
若出现1->2(权值为1)2->1(权值-1)的环,我们在处理的时候会把他的环大小变为(1-0-1=0),而0与任何数的公因数都是任何数,不会造成影响。
对于其他的“不成立”情况,可以根据这个代码自行模拟一下,很快就会发现他的正确性。
2.判链过程中:
对于链,只有一种不成立的情况,就是链本身的长度小于3,这种情况我们就好判了:
Min保存的是这个点向前延伸的最远长度(负数),Max保存的是这个点向后延伸的最远长度,两者一减,再加上这个点自己,就是这条链的长度,我们记录所有链的长度之和。我们在这里没有直接输出所有点数的原因是,同一个点有可能处于多条链的交汇处,而根据题目条件,一个点指向的所有点和指向一个点的所有点编号相同,不能认为每一个人的面具都不同,而是一个“单链”中的面具都不同,我们自然要保存每一组相交的单链中最长的那个。

void dfs_lian(int u){ vis[u]=1; Max=max(Max,dis[u]); Min=min(Min,dis[u]); for(int i=head[u];~i;i=edge[i].next){ int v=edge[i].to; if(!vis[v]){ dis[v]=dis[u]+edge[i].val; dfs_lian(v); } } } int main(){ for(int i=1;i<=n;i++){ if(!vis[i]){ Max=Min=dis[i]=0; dfs_lian(i); ans+=Max-Min+1; } } if(ans>=3){ printf("%d 3 ",ans); }else printf("-1 -1 "); return 0; }
下面附上全代码:

#include<bits/stdc++.h> using namespace std; const int maxn=2e6+20; int n,m; struct E{ int to,val,next; }edge[maxn]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } int gcd(int x,int y){ if(y==0)return x; if(x==0)return y; if(x%y==0)return y; return gcd(y,x%y); } int vis[maxn],dis[maxn],ans; void dfs_huan(int u){ vis[u]=1; for(int i=head[u];~i;i=edge[i].next){ int v=edge[i].to; if(!vis[v]){ dis[v]=dis[u]+edge[i].val; dfs_huan(v); }else{ ans=gcd(ans,abs(dis[u]-dis[v]+edge[i].val)); } } } int Max,Min; void dfs_lian(int u){ vis[u]=1; Max=max(Max,dis[u]); Min=min(Min,dis[u]); for(int i=head[u];~i;i=edge[i].next){ int v=edge[i].to; if(!vis[v]){ dis[v]=dis[u]+edge[i].val; dfs_lian(v); } } } int main(){ scanf("%d%d",&n,&m); memset(head,-1,sizeof(head)); for(int i=1;i<=m;i++){ int from,to; scanf("%d%d",&from,&to); add(from,to,1); add(to,from,-1); } for(int i=1;i<=n;i++){ if(!vis[i]){ dfs_huan(i); } } if(ans!=0){ if(ans<3){ printf("-1 -1 "); return 0; }else{ int i; for(i=3;i<=ans;i++){ if(ans%i==0){ break; } } printf("%d %d ",ans,i); return 0; } } memset(vis,0,sizeof(vis)); ans=0; for(int i=1;i<=n;i++){ if(!vis[i]){ Max=Min=dis[i]=0; dfs_lian(i); ans+=Max-Min+1; } } if(ans>=3){ printf("%d 3 ",ans); }else printf("-1 -1 "); return 0; }
(dark假期集训%拟赛2)Layout(差分约束)(洛谷P4878)
这算比较基础的差分约束题目了。
比较明显的约束关系:
a牛与b牛互相爱慕:d[b]-d[a]<=z(b在a后面)
a牛与b牛互相讨厌:d[b]-d[a]>=z (b在a后面)
编号小的牛要在编号编号大的牛前面:d[i]-d[i-1]>=0
题目要求1到n的最大值,我们全部转化成<=,求最短路即可
这里还有一个问题,就是有可能从1开始spfa并不能遍历到每一个点(图不联通),而在与1不联通的地方有可能存在负环,我们想解决这个问题,只需要建一个虚拟的超级源点,由他向每一个点建边,这样再跑它的spfa就可以找全图的负环了,没有负环再跑spfa(1)找结果即可。
代码:

#include<bits/stdc++.h> using namespace std; const int maxn=50010; struct E{ int to,val,next; }edge[maxn]; int head[maxn],tot; void add(int from,int to,int val){ edge[++tot].to=to; edge[tot].val=val; edge[tot].next=head[from]; head[from]=tot; } int n,m,k,flag; int dis[maxn],vis[maxn],cnt[maxn]; queue<int> q; void spfa(int s){ memset(dis,0x3f,sizeof(dis)); memset(vis,0,sizeof(vis)); memset(cnt,0,sizeof(cnt)); dis[s]=0; q.push(s); while(!q.empty()){ int u=q.front();q.pop();vis[u]=0; for(int i=head[u];i;i=edge[i].next){ int v=edge[i].to; if(dis[v]>dis[u]+edge[i].val){ dis[v]=dis[u]+edge[i].val; if(!vis[v]){ if(++cnt[v]>n){ flag=-1; return; } vis[v]=1;q.push(v); } } } } if(dis[n]==0x3f3f3f3f)flag=-2; } int main(){ scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=m;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); if(from>to)swap(from,to); add(from,to,val); }//互相爱慕的牛我们由较小编号的向较大编号的建正权边 //d[to]-d[from]<=val 我们由from向to建边(视个人喜好) for(int i=1;i<=k;i++){ int from,to,val; scanf("%d%d%d",&from,&to,&val); if(from>to)swap(from,to); add(to,from,-val); }//互相讨厌的牛我们由较大编号的向较小编号的建负权边 //d[to]-d[from]>=val------->d[from]-d[to]<=-val我们由to向from建边 for(int i=2;i<=n;i++){ add(i,i-1,0); }//d[i]-d[i-1]>=0-------->d[i-1]-d[i]<=0我们由i向i-1建边 //上面这三个无所谓谁向谁建边,只要三个保持一致就好了(指减号前面的都在有向边的同一侧) //像这样建边我们spfa(1)找dis[n],如果反着来spfa(n)找dis[1]即可。 for(int i=1;i<=n;i++){ add(0,i,0); }//超级源点(0)向所有点建边 spfa(0); if(flag==-1){ printf("-1"); return 0; } spfa(1); if(flag==-1)dis[n]=-1; if(flag==-2)dis[n]=-2; printf("%d",dis[n]); return 0; }
(dark假期集训%拟赛2)游戏(反向并查集)
题目:

分析:
我们从题目中可以发现:每一个点只有一个出边。这类似与我们的并查集的父亲结点,每一个点的父亲结点只有一个。所以这道题我们可以用并查集做。
1.通过Find操作,我们可以找到一个点的最早祖先,也就是这个点最后停止的点,如果有环的话特判一下。
2.可是这道题是边查边删除边的,所以我们需要用一个并查集技巧:离线并查集之删边等于倒着加边大概就是正着删除边等于倒着加边,我们可以倒序处理这些查询,先在输入的时候把该删的边全删掉,再倒着加回来,边加边查。至于为什么不能边删边查,是因为并查集的优化中有一个路径压缩,它会打破之前所建的边的关系,但是不影响结果,删边操作不满足路径压缩,加边是满足的(就是加边之后原来的祖先还是祖先,顶多不是最早的,但是删边之后,你的祖先有可能就不是你的祖先了)。
上代码:

#include<bits/stdc++.h> using namespace std; const int maxn=3e5+10; int fa[maxn],n,q,Time,res[maxn],now[maxn],mode[maxn],ans[maxn]; int find(int x,int Time){ if(Time>n){ return fa[x]=0; } //判环的特判:如果循环的次数大于n,一定有环。 //fa[x]=0的作用是把这个环从这里断开,避免以后重复判环造成时间冗余(不这么些你就T了) //以后的点再判到这个环时,会到这个断点,然后再运行到fa[0]=0,这样就表示有环了,与下面的环的特判相结合 if(fa[x]==x)return x; else return fa[x]=find(fa[x],Time+1); } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ int xx; scanf("%d",&xx); if(xx==0)fa[i]=i; else res[i]=fa[i]=xx; }//因为回头要加边,所以先保存一下每个点的父亲 scanf("%d",&q); for(int i=1;i<=q;i++){ scanf("%d%d",&mode[i],&now[i]); if(mode[i]==2){ fa[now[i]]=now[i]; //删边 } } int cnt=0; for(int i=q;i>=1;i--){ if(mode[i]==1){ ans[++cnt]=find(now[i],0); //加入答案中 }else{ fa[now[i]]=res[now[i]]; //恢复边 } } for(int i=cnt;i>=1;i--){ if(ans[i]==0)printf("CIKLUS ");//环 else printf("%d ",ans[i]); } //倒着保存的,所以要倒着输出才是正过来的答案 return 0; }
(dark假期集训%拟赛3)乘车路线(二维限制最短路)
题目:

基本就是最短路板子了,但是又多了一个限制条件,根据隔壁dp的尿性,多一个限制就多一维呗
我们定义dp[i][j](串味了),dis[i][j]表示i点在花j的费用的条件下距离起点的最短距离。
我们的spfa也需要作出一些改变,队列里面保存的不只是点的编号,还有它到起始点的花费。比较的时候也要特判当前的cost是否已经超过了限制的花费。
上代码:

#include<bits/stdc++.h> using namespace std; typedef long long LL; const int maxn=100010; int n,m,w; struct E{ int from,to,v,c,next; }edge[maxn]; //既然是二维了,那么建边的时候也要多一个变量 int head[1100],tot; void add(int from,int to,int v,int c){ edge[++tot].to=to; edge[tot].v=v; edge[tot].c=c; edge[tot].next=head[from]; head[from]=tot; } struct Node{ int node,cost; //node表示点的编号,cost表示点的花费 Node(){} Node(int x,int y){ node=x;cost=y; } }; int dis[1100][1100],vis[1100][1100],Min=0x7fffffff; queue<Node> q; //dis、vis数组都变成二维,队列也多保存一个花费 void spfa(int s){ memset(dis,0x3f,sizeof(dis)); dis[s][0]=0; //起点花费和距离肯定都是0 q.push(Node(s,0)); while(!q.empty()){ Node u=q.front();q.pop();vis[u.node][u.cost]=0; for(int i=head[u.node];i;i=edge[i].next){ int v=edge[i].to; int val=edge[i].v,c=edge[i].c; if(u.cost+c>w)continue;//超出费用限制直接continue掉 if(dis[v][u.cost+c]>dis[u.node][u.cost]+val){//当前花费是上一个点的花费+这条边的花费 dis[v][u.cost+c]=dis[u.node][u.cost]+val;//其他部分跟spfa没啥区别 if(!vis[v][u.cost+c]){ q.push(Node(v,u.cost+c)); vis[v][u.cost+c]=1; } } } } } int main(){ scanf("%d%d%d",&w,&n,&m); for(int i=1;i<=m;i++){ int from,to,v,c; scanf("%d%d%d%d",&from,&to,&v,&c); add(from,to,v,c); } spfa(1); for(int i=0;i<=w;i++){ Min=min(Min,dis[n][i]); //在到终点的不同花费中找最小的路程 } if(Min==0x3f3f3f3f){ printf("NO "); return 0; } printf("%d",Min); return 0; }
