点分治学习笔记

写在前面

先开个坑...

之前学过点分治，但是总是感觉打的时候内心莫名的慌，敲完几个函数的定义就开始脑袋一片空白。

所以重学了一下点分治，并写了这篇博客。

看看什么时候把它补完吧。

---

(mathrm{1}) 参考资料

找了两篇还不错的博客

https://www.cnblogs.com/bztMinamoto/p/9489473.html

https://www.cnblogs.com/PinkRabbit/p/8593080.html

---

(mathrm{2}) 问题提出

考虑这样一个问题：给出一棵树，求有多少个点对 ((x,y)) 满足它们之间的距离不超过 (k) / 等于 (k) / 大于 (k)。

(1 le n le 10^5)

(mathrm{2.1}) 暴力解法一

很显然，求两个点点对数目，可以枚举这两个点，然后求它们的距离。

时间复杂度 (O(n^3)) ，如果命题人给了这个复杂度超过 (20pts) 可真是良心。

(mathrm{2.2}) 暴力解法二

可以枚举起点 (x) ，然后遍历这棵树，一旦距离超过 (k) 就返回。

如果是求大于 (k) 的，就先求出小于等于 (k) 的，然后容斥。

时间复杂度 (O(n^2)) ，正常的命题人应该会给到 (30pts-60pts) 。

(mathrm{2.3}) 正解

点分治。

---

(mathrm{3}) 点分治

(mathrm{3.1}) 点分治思想和理解

点分治，顾名思义，是一种与点有关的分治算法。

分治分治，分而治之。树形结构是一种有序的结构，其有一种自然的，从上往下的秩序，分治自然按照这样的顺序进行。

但是如果我们就以 (1) 为根，可以被菊花图卡到 (O(n^2)) ？所以我们不能以 (1) 为根。

但是选择的这个根肯定不能是随机的不然得分也是随机的。考虑树上的特殊的点，自然想到树的重心。树的重心保证了删掉它之后，最大的子树不超过 (frac{n}{2}) ，所以复杂度上界是 (O(n log n)) 的。

因此，点分治的代码中，自然有 getroot 函数。

我们称当前选择的这个重心为 当前的分治中心

每次的分治中心分治完后，我们继续向它的子树分治，因此每一个 分治中心 会把当前的 分治区域 分为若干个 新的更小的分治区域 ，这就是大规模问题向类似的小规模问题转化的过程，也符合点分治名字中 分治 的意义。

(mathrm{3.2}) 点分治实现

首先给出点分治的流程：

1. 求树的重心
2. 以树的重心为分治中心为根开始点分治
3. 寻找当前分治块的重心，作为分治中心
4. 删除当前分治中心，计算当前分治中心答案的贡献，删除重复贡献。
5. 在删除当前分治中心产生的联通块中继续分治，重复3-5，直到无法分治

流程代码：

void dfs(int x){
	ans+=calc(x,0);del[x]=1;
	for(int i=Head[x];i;i=Next[i]){
		int y=to[i];
		if(del[y]) continue;
		ans-=calc(y,w[i]);
		sz=size[y],mx=INF;
		getroot(y,0);dfs(root);
	}
}

其中比较难以理解的语句为

ans-=calc(y,w[i]);

将在后面的博文中解释。

上述代码中，calc 为计算答案的代码，因题而异， del 表示删除当前分治中心，getroot 为寻找重心， sz 为当前分治块的大小。

其中 size 等需要预处理。

(mathrm{3.3}) 删除重复贡献

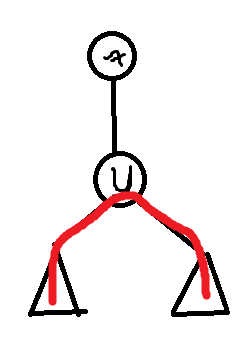
对于红色的这样一条路径，从 (y) 的某个子树中经过 (y) ，进入 (y) 的另外一个子树的一条有贡献的路径，在 (x) 的时候可能会：

重复经过一条边，导致被多次计算。

---

(mathrm{4}) 一些例题

POJ