二叉树有一般二叉树、完全二叉树、满二叉树、霍夫曼树等。结点是数据结构中的基础,是构成复杂数据结构的基本组成单位。

结点A。
树
树是一种数据结构。其中一个元素可以有两个或者多个数据元素,具有一对多的特点,用树结构来存储文件。
树是(n>=0)个结点的有限集。n=0时称为空树。
在任意一颗非空树中:有且仅有一个特定的为根的结点。
当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1、T2、T3、……、Tn,其中每一个集合本身又是一棵树,并且称为根的子树。
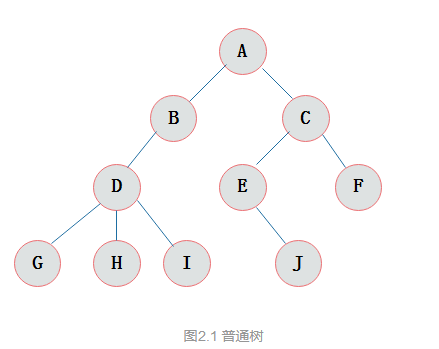
结点的度:结点拥有的子树数目称为结点的度。
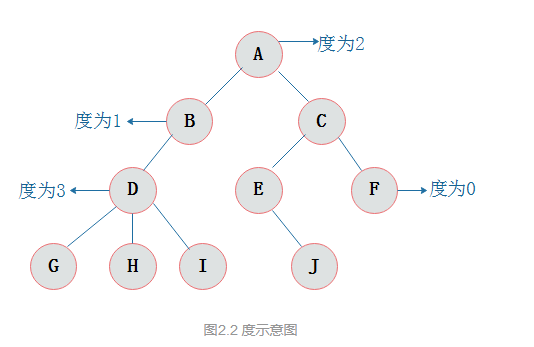
结点子树的根结点为该结点的孩子结点。
相应该结点称为孩子结点的双亲结点。
如上图A为B的双亲结点,B为A的孩子结点。
同一个双亲结点的孩子结点之间互称兄弟结点。
结点B与结点C互称兄弟结点。
结点层次:从根开始定义起,根为第一层,根的孩子为第二层,以此类推。
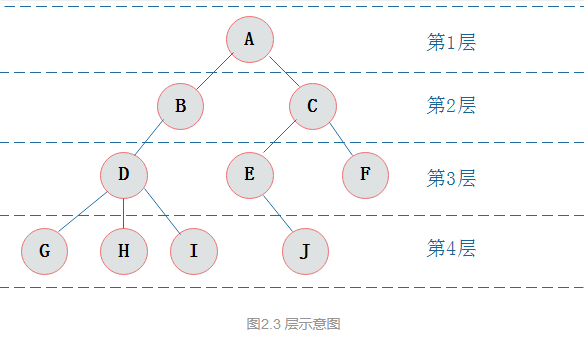
树的深度:树中结点的最大层次数称为树的深度或者高度。上图中树的深度是4。
二叉树
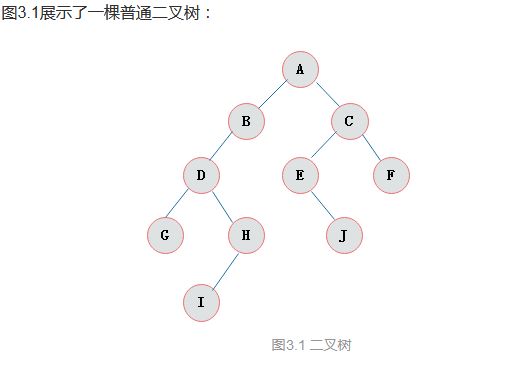
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”和“右子数”。
二叉树是树的特殊一种。具有如下特点:
a.每个结点最多有两颗子树,结点的度最大为2.
b.左子树和右子树是有顺序的,次序不能颠倒。
c.即使某个结点只有一个子树,也要区分左右子树。
二叉树有五种基本形态:
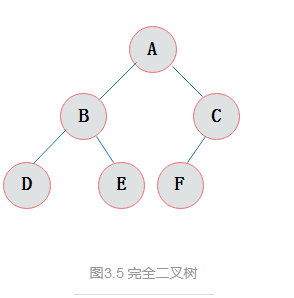
空二叉树、只有一个根节点的二叉树、只有左子树、只有右子树、完全二叉树。

满二叉树一定是完全二叉树。
二叉树存储结构:顺序结构
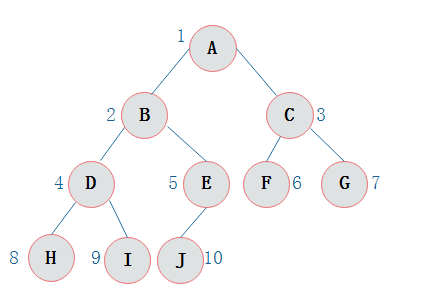

二叉树的遍历:前序遍历、中序遍历、后序遍历和层序遍历。
前序遍历通俗的说就是从二叉树的根结点出发,当第一次到达结点时就输出结点数据,按照先向左再向右的方向访问。
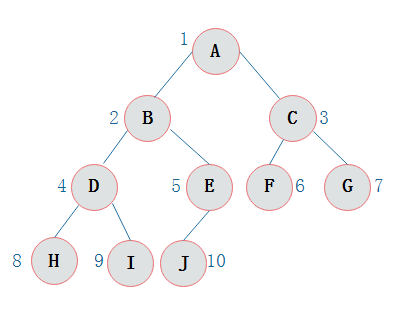
输出结果是:ABDHIEJCFG
中序遍历从二叉树的根结点出发,当第二次到达结点时就输出结点数据,按照先向左向右方向访问。
输出顺序为:HDIBJEAFCG
后序遍历是从二叉树的根结点出发,第三次到达结点就输出结点数据,按照先向左再向右的方向访问。
输出循序:HIDJEBFGCA
层次遍历就是按照树的层次自上而下的遍历二叉树。输出循序为:ABCDEFGHIJ。