秋招各大厂，必考的优先队列和堆排序

　　秋招过了，春招还会远么？真实面试题：工作一年同事跳槽，去某为，就考了一道：用数组实现堆排序，下面就来介绍一下堆排序的实现

　堆和优先队列

　　堆的定义　

n个元素的序列k={k0,k1,……,kn-1},当且仅满足条件

(1)ki >= k2i+1 和 ki >= k2i+2      (2)ki <= k2i+1 和 ki <= k2i+2

(1)称为大根堆 (2)称为小根堆

可以把堆看成完全二叉树。

　　优先队列

优先队列是一种常见的抽象数据类型，它与"队列"不同，不遵循"先进先出"原则，而遵循"最大元素先出"原则，出队和优先级有关。 

优先队列的基本操作有三个：

(1) 向优先队列里插入一个元素

(2) 在优先队列找出最大元素

(3) 删除优先队列中最大元素

可以用堆来实现优先队列

　 二叉堆　　

　　最大堆定义

　　堆中任一节点总是大于其父节点的值，堆总是一颗完全二叉树，本篇博客以实现最大堆为主

　　数组实现二叉堆

　　用二叉树来实现堆，是比较好的，也可以用二叉树的左右指针来实现，但这种太麻烦；因为是完全二叉树，所以也可以用数组来实现二叉堆，见下图：　　PS：依旧是全博客园最丑图

　　

 　　

　　　　

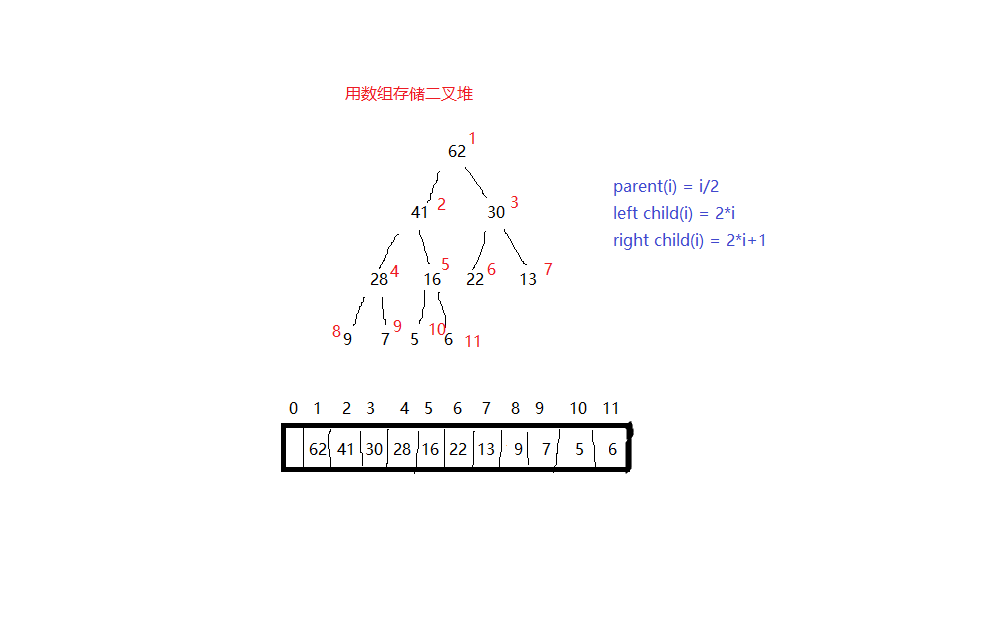
 　　说明：将数组的值来抽象成二叉树，二叉树图上的红色字就表示数组的下标，而且还能总结出蓝色字体的规律。

　　构建一个堆类，代码如下：

　　

template<typename Item>
class MaxHeap{
private:
    Item *data;    //数组
    int count;    //堆的大小
    int capacity;    //堆的容量
public:
    //构造函数 构建一个空堆
    MaxHeap(int capacity){

        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }
}；

　　

　　最大堆的实现

　　最大堆上插入元素 shift up

　　直接上图，再说明，如下图：

　　

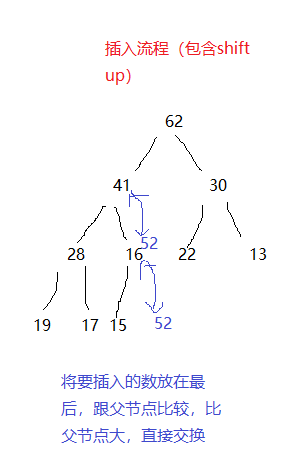
　　代码如下：

　　

 void shiftUp(int k){
        while(k>1 && data[k/2]<data[k]){
            swap(data[k/2],data[k]);
            k /= 2;
        }
    }

//向最大堆中插入元素
    void insert(Item item){
        assert(count+1<=capacity);
        data[count+1] = item;
        shiftUp(count+1);
        count++;
    }

　　

　　最大堆上取出元素 shift down

　　直接上图，如下：

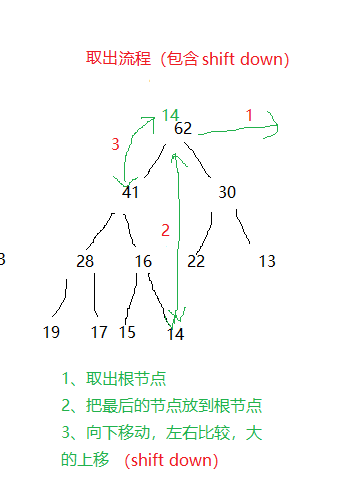
　　代码如下：

　　

void shiftDown(int k){
        while(2*k<=count){
            int j = 2*k;
            if(j+1<count && data[j+1]>data[j]) j++; //右孩子比左孩子，j移动
            if(data[k]>data[j]) break;
            swap(data[k],data[j]);
            k=j;
        }
    }

//从最大堆中取出堆顶元素
    Item extracMax(){
        assert(count > 0);
        Item ret = data[1];
        swap(data[1],data[count]);
        count--;
        shiftDown(1);
        return ret;
    }

　　实现堆排序

　　有了插入和取出，就可以实现堆排序了，代码如下：

　　

//将所有元素插入堆，再取出
template<typename T>
void heapSort1(T arr[],int n){

    MaxHeap<T> maxheap = MaxHeap<T>(n); 
    for(int i=0;i<n;i++)
        maxheap.insert(arr[i]);

    //从小到大排序
    for(int i=n-1;i>=0;i--)
        arr[i] = maxheap.extracMax();

}

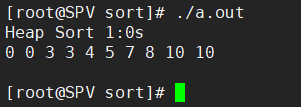
　　运行结果如下：

　　

　　

　　heapify实现最大堆

　　构造函数实现heapify过程　　

就是用构造函数来实现最大堆，见下图：

 

　　

 

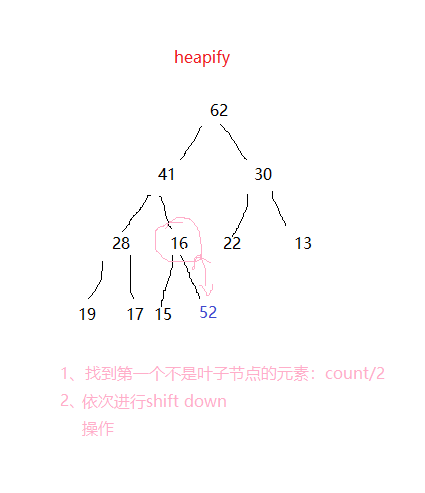
　　代码如下：

//构造函数，通过给定数组实现最大堆 O(n)
    MaxHeap(Item arr[],int n){
        
        data = new Item[n+1];
        capacity = n;

        for(int i=0;i<n;i++)
            data[i+1] = arr[i];
        count = n;

        for(int i=count/2;i>=1;i--)
            shiftDown(i);
    }

// heapSort2, 借助我们的heapify过程创建堆
// 此时, 创建堆的过程时间复杂度为O(n), 将所有元素依次从堆中取出来, 实践复杂度为O(nlogn)
// 堆排序的总体时间复杂度依然是O(nlogn), 但是比上述heapSort1性能更优, 因为创建堆的性能更优
template<typename T>
void heapSort2(T arr[], int n){

    MaxHeap<T> maxheap = MaxHeap<T>(arr,n);
    for( int i = n-1 ; i >= 0 ; i-- )
        arr[i] = maxheap.extracMax();

}

　　

　　总体代码

　　Heap.h头文件，代码如下：

　　

#ifndef HEAP_H_
#define HEAP_H_

#include<algorithm>
#include<cassert>
using namespace std;

template<typename Item>
class MaxHeap{
private:
    Item *data;    //数组
    int count;    //堆的大小
    int capacity;    //堆的容量

    void shiftUp(int k){
        while(k>1 && data[k/2]<data[k]){
            swap(data[k/2],data[k]);
            k /= 2;
        }
    }

    void shiftDown(int k){
        while(2*k<=count){
            int j = 2*k;
            if(j+1<count && data[j+1]>data[j]) j++; //右孩子比左孩子，j移动
            if(data[k]>data[j]) break;
            swap(data[k],data[j]);
            k=j;
        }
    }
public:
    //构造函数 构建一个空堆
    MaxHeap(int capacity){

        data = new Item[capacity+1];
        count = 0;
        this->capacity = capacity;
    }

    //构造函数，通过给定数组实现最大堆 O(n)
    MaxHeap(Item arr[],int n){
        
        data = new Item[n+1];
        capacity = n;

        for(int i=0;i<n;i++)
            data[i+1] = arr[i];
        count = n;

        for(int i=count/2;i>=1;i--)
            shiftDown(i);
    }

    ~MaxHeap(){
        delete[] data;
    }

    //返回堆中的元素个数
    int size(){
        return count;
    }

    //判断是否为空
    bool isEmpty(){
        return count==0;
    }

    //向最大堆中插入元素
    void insert(Item item){
        assert(count+1<=capacity);
        data[count+1] = item;
        shiftUp(count+1);
        count++;
    }

    //从最大堆中取出堆顶元素
    Item extracMax(){
        assert(count > 0);
        Item ret = data[1];
        swap(data[1],data[count]);
        count--;
        shiftDown(1);
        return ret;
    }

};

#endif

　　heap.cpp如下：

　　

#include<iostream>
#include<algorithm>
#include"Heap.h"
#include "SortTestHelper.h"

//将所有元素插入堆，再取出
template<typename T>
void heapSort1(T arr[],int n){

    MaxHeap<T> maxheap = MaxHeap<T>(n); 
    for(int i=0;i<n;i++)
        maxheap.insert(arr[i]);

    //从小到大排序
    for(int i=n-1;i>=0;i--)
        arr[i] = maxheap.extracMax();

}


// heapSort2, 借助我们的heapify过程创建堆
// 此时, 创建堆的过程时间复杂度为O(n), 将所有元素依次从堆中取出来, 实践复杂度为O(nlogn)
// 堆排序的总体时间复杂度依然是O(nlogn), 但是比上述heapSort1性能更优, 因为创建堆的性能更优
template<typename T>
void heapSort2(T arr[], int n){

    MaxHeap<T> maxheap = MaxHeap<T>(arr,n);
    for( int i = n-1 ; i >= 0 ; i-- )
        arr[i] = maxheap.extracMax();

}

int main(){
    
    int n = 10;
    
    
    // 测试1 一般性测试
    //cout<<"Test for random array, size = "<<n<<", random range [0, "<<n<<"]"<<endl;
    int* arr1 = SortTestHelper::generateRandomArray(n,0,n);
    int* arr2 = SortTestHelper::copyIntArray(arr1, n);
        
    SortTestHelper::testSort("Heap Sort 1", heapSort1, arr1, n);
    SortTestHelper::testSort("Heap Sort 2", heapSort2, arr2, n);
    
    for(int i=0;i<n;i++)
        cout << arr1[i] << " ";
    cout << endl;
    
    for(int i=0;i<n;i++)
        cout << arr2[i] << " ";
    cout << endl;

    delete[] arr1;
    delete[] arr2;
    cout <<endl;
}

　　

　　十一月总结

　　正如前面所说：秋招已过，春招还会远么？18年还有一个月就要结束了，感觉比大学时过的时间还快！有个战略要改变，之前定的年底之前一直要学数据结构和算法，这个计划要伴随整个职业生涯了，最起码一直到明年5月，都要一直坚持学！

　　11月主要完成的

• 　　学了python
•         数据结构和算法完成了整体架构的学习和整理
•         复习C++和操作系统

　　12月计划

• 　　最主要的计划就是有效深入的学习数据结构和算法
•        巩固C++、操作系统和网络编程

　　

　　2018年最后一个月了，大家加油！