树的广度优先搜索(上):人际关系的六度理论是真的吗?
社交网络中的好友问题
LinkedIn、Facebook、微信、QQ 这些社交网络平台都有大量的用户。在这些社交网络中,非常重要的一部分就是人与人之间的“好友”关系。
在数学里,为了表示这种好友关系,我们通常使用图中的结点来表示一个人,而用图中的边来表示人和人之间的相识关系,那么社交网络就可以用图论来表示。而“相识关系”又可以分为单向和双向。
单向表示,两个人 a 和 b,a 认识 b,但是 b 不认识 a。如果是单向关系,我们就需要使用有向边来区分是 a 认识 b,还是 b 认识 a。如果是双向关系,双方相互认识,因此直接用无向边就够了。
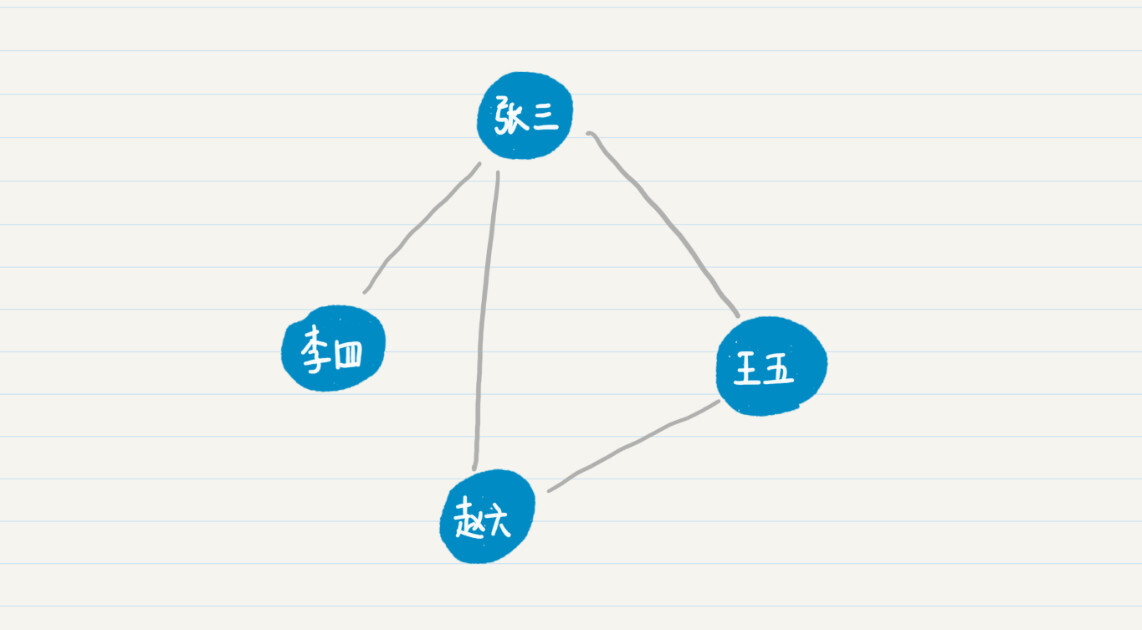
从上面的例图可以看出,人与人之间的相识关系,可以有多条路径。比如,张三可以直接连接赵六,也可以通过王五来连接赵六。比较这两条通路,最短的通路长度是 1,因此张三和赵六是一度好友。也就是说,这里我用两人之间最短通路的长度,来定义他们是几度好友。照此定义,在之前的社交关系示意图中,张三、王五和赵六互为一度好友,而李四和赵六、王五为二度好友。
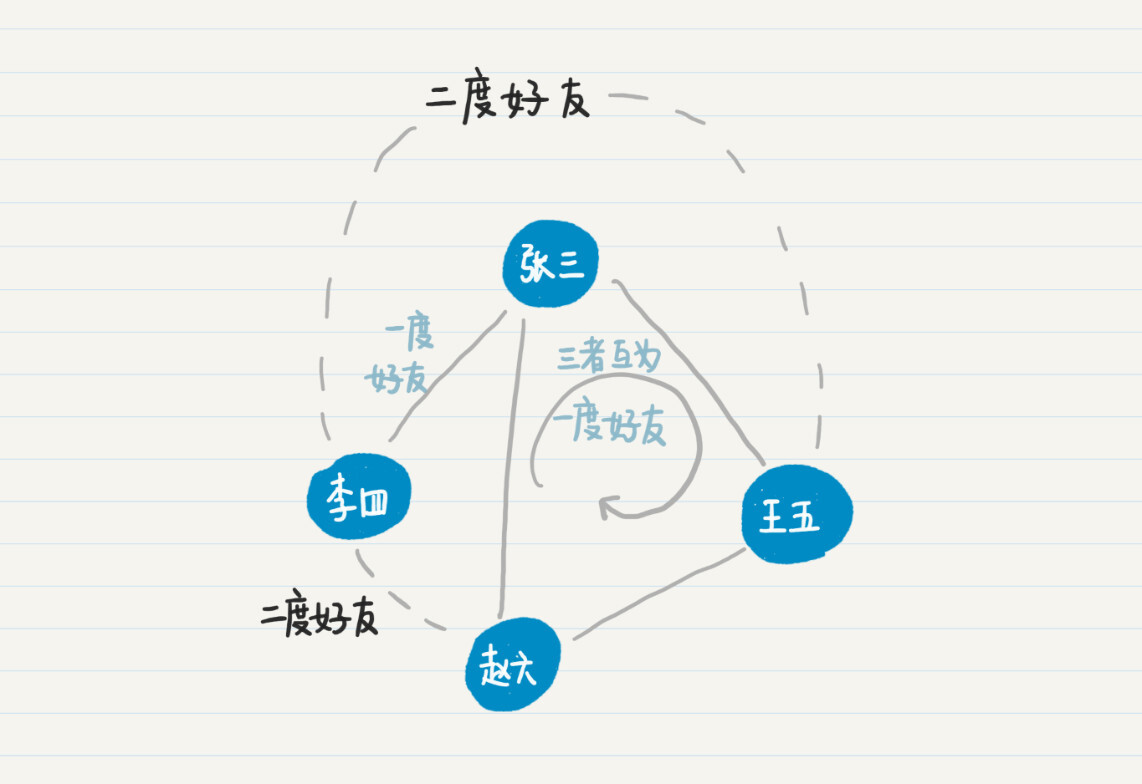
给定一个用户,如何优先找到他的二度好友呢?
深度优先搜索面临的问题
在使用深度优选搜索的时候,一旦遇到产生回路的边,我们需要将它过滤。具体的操作是,判断新访问的点是不是已经在当前通路中出现过,如果出现过就不再访问。
六度理论告诉我们,你的社会关系会随着关系的度数增加,而呈指数级的膨胀。这意味着,在深度搜索的时候,每增加一度关系,就会新增大量的好友。
什么是广度优先搜索?
广度优先搜索(Breadth First Search),也叫宽度优先搜索,是指从图中的某个结点出发,沿着和这个点相连的边向前走,去寻找和这个点距离为 1 的所有其他点。只有当和起始点距离为 1 的所有点都被搜索完毕,才开始搜索和起始点距离为 2 的点。当所有和起始点距离为 2 的点都被搜索完了,才开始搜索和起始点距离为 3 的点,如此类推。
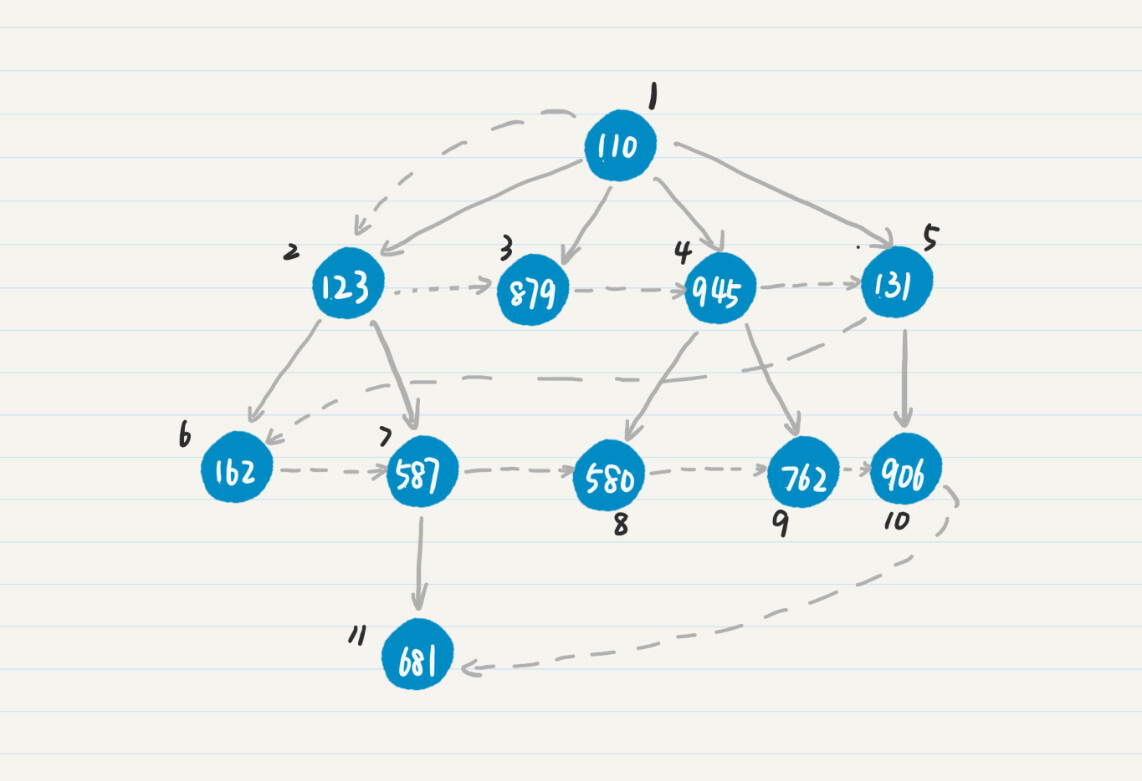
广度优先搜索其实就是横向搜索一颗树啊!
尽管广度优先和深度优先搜索的顺序是不一样的,它们也有两个共同点。
第一,在前进的过程中,我们不希望走重复的结点和边,所以会对已经被访问过的点做记号,而在之后的前进过程中,就只访问那些还没有被标记的点。这一点上,广度优先和深度优先是一致的。有所不同的是,在广度优先中,如果发现和某个结点直接相连的点都已经被访问过,那么下一步就会看和这个点的兄弟结点直接相连的那些点,从中看看是不是有新的点可以访问。
在上图中,访问完结点 945 的两个子结点 580 和 762 之后,广度优先策略发现 945 没有其他的子结点了,因此就去查看 945 的兄弟结点 131,看看它有哪些子结点可以访问,因此下一个被访问的点是 906。而在深度优先中,如果到了某个点,发现和这个点直接相连的所有点都已经被访问过了,那么不会查看它的兄弟结点,而是回退到这个点的父节点,继续查看和父结点直接相连的点中是不是存在新的点。例如在上图中,访问完结点 945 的两个子结点之后,深度优先策略会回退到点 110,然后访问 110 的子结点 131。
第二,广度优先搜索也可以让我们访问所有和起始点相通的点,因此也被称为广度优先遍历。如果一个图包含多个互不连通的子图,那么从起始点开始的广度优先搜索只能涵盖其中一个子图。这时,我们就需要换一个还没有被访问过的起始点,继续广度优先遍历另一个子图。广度优先搜索可以使用同样的方式来遍历有多个连通子图的图,
如何实现社交好友推荐?
如何在记录所有已被发现的结点情况下,优先访问距离更短的点呢?仔细观察,你会发现和起始点更近的结点,会先更早地被发现。也就是说,越早被访问到的结点,越早地处理它,
这里我们需要用到队列这种先进先出(First In First Out)的数据结构。
那么在广度优先搜索中,队列是如何工作的呢?这主要分为以下几个步骤。
首先,把初始结点放入队列中。然后,每次从队列首位取出一个结点,搜索所有在它下一级的结点。接下来,把新发现的结点加入队列的末尾。重复上述的步骤,直到没有发现新的结点为止。
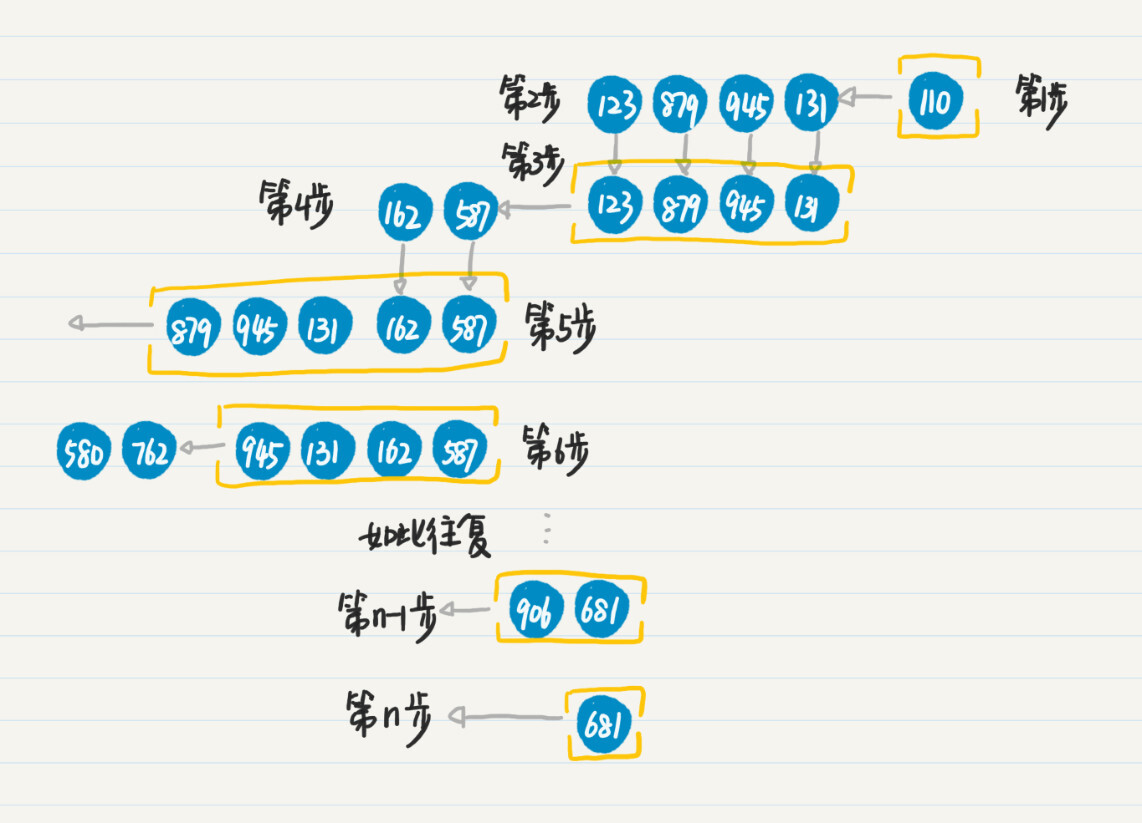
第 1 步,将初始结点 110 加入队列中。
第 2 步,取出结点 110,搜出下一级结点 123、879、945 和 131。
第 3 步,将点 123、879、945 和 131 加入队列的末尾。
第 4 步,重复第 2 和第 3 步,处理结点 123,将新发现结点 162 和 587 加入队列末尾。
第 5 步,重复第 2 和第 3 步,处理结点 879,没有发现新结点。
第 6 步,重复第 2 和第 3 步,处理结点 945,将新发现的结点 580 和 762 加入队列末尾。
……
第 n-1 步,重复第 2 和第 3 步,处理结点 906,没有发现新结点。
第 n 步,重复第 2 和第 3 步,处理结点 681,没有发现新的结点,也没有更多待处理的结点,整个过程结束。
- 用户结点 Node。这次设计的用户结点和前缀树结点 TreeNode 略有不同,包含了用户的 ID user_id,以及这个用户的好友集合。我用 HashSet 实现,便于在生成用户关系图的时候,确认是否会有重复的好友。
- 表示整个图的结点数组 Node[]。由于每个用户使用 user_id 来表示,所以我可以使用连续的数组表示所有的用户。用户的 user_id 就是数组的下标。
- 队列 Queue。由于 Java 中 Queue 是一个接口,因此需要用一个拥有具体实现的 LinkedList 类。
总结
在遍历树或者图的时候,如果使用深度优先的策略,被发现的结点数量可能呈指数级增长。如果我们更关心的是最近的相连结点,比如社交关系中的二度好友,那么这种情况下,广度优先策略更高效。也正是由于这种特性,我们不能再使用递归编程或者栈的数据结构来实现广度优先,而是需要用到具有先进先出特点的队列。
