摘要:本文先从梯度下降法的理论推导开始,说明梯度下降法为什么能够求得函数的局部极小值。通过两个小例子,说明梯度下降法求解极限值实现过程。在通过分解BP神经网络,详细说明梯度下降法在神经网络的运算过程,并详细写出每一步的计算结果。该过程通俗易懂,有基本的高数和线代基础即可理解明白。最后通过tensorflow实现一个简单的线性回归,对照理解梯度下降法在神经网络中的应用。码字不易,转载请标明出处。该文中部分内容是研究生课堂论文内容,为避免课程论文被误解为抄袭,所用截图特意添加水印。
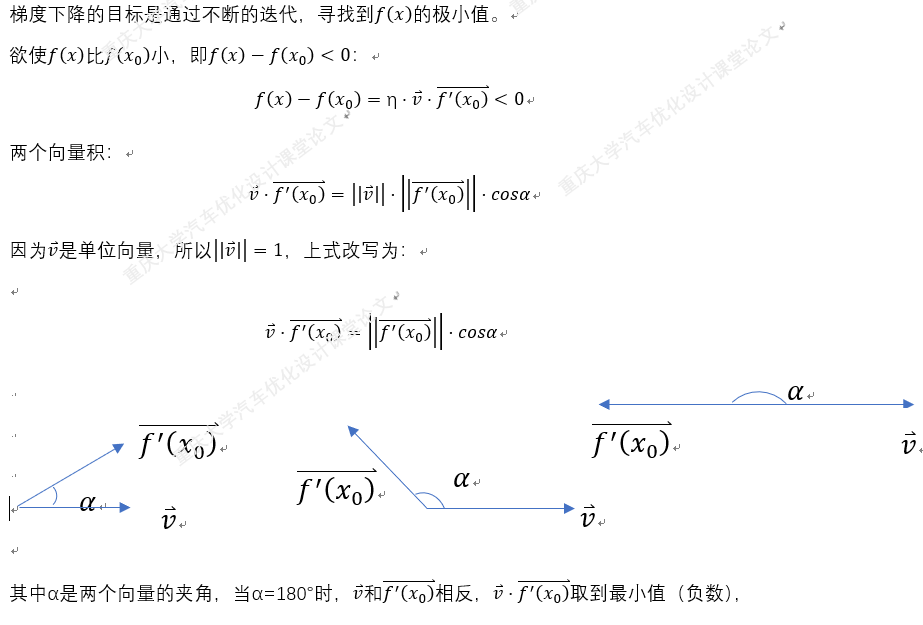
一.梯度下降法的理论推导:


二.求解一个简单的一元函数极小值
例:求函数y=(x+1)^2-1的极小值:
实现环境:python3.6
相关模块:numpy 、 matplotlib

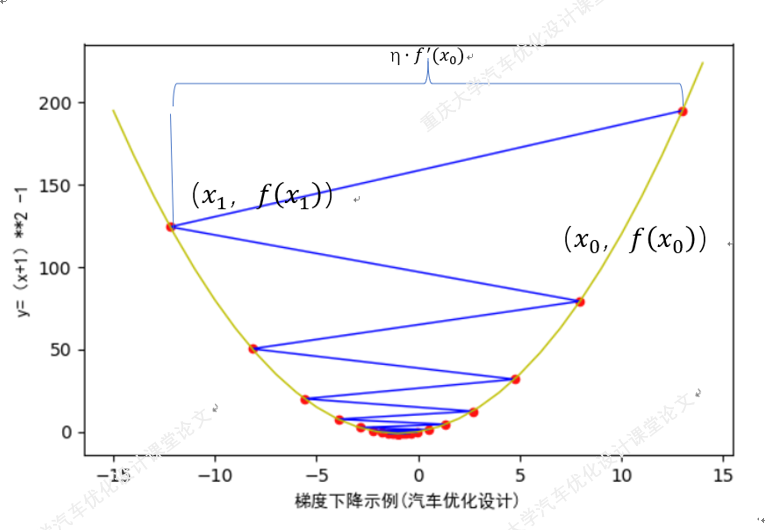
import numpy as np from matplotlib import pyplot as plt def function_1d(x): ''' 目标函数:求目标函数的极小值 x:自变量,标量 返回:因变量,标量 ''' return (x+1)**2-1 ##2.定义梯度函数 def grad_1d(x): ''' :param x: 自变量,标量 :return: 因变量,标量 ''' return 2*(x+1) ##3.定义迭代过程 def gradient_descent_1d(grad,current_x,learning_rate=0.0001,precision=0.0001,max_iters=10000): ''' 一维问题的梯度下降法 :param grad: 目标函数的梯度 :param current_x: 当前x值 :param learning_rate: 学习率=η :param precision: 收敛精度 :param max_iters: 最大迭代次数 :return: 极小值 ''' ##创建一个空列表用于接收每次移动后的current_x cur_x_list = [] cur_x_list.append(current_x) for i in range(max_iters): grad_current = grad(current_x) if abs(grad_current)<precision: break ##梯度小于收敛精度时,视为收敛 current_x = current_x-grad_current*learning_rate cur_x_list.append(current_x) print('第%s次迭代:x=%s'%(i,current_x)) print('极小值点(%s,%s)'%(current_x,function_1d(current_x))) return cur_x_list ##4.运行返回极小值和x移动轨迹 if __name__ == '__main__': cur_x_list = gradient_descent_1d(grad_1d,learning_rate=0.9,current_x=13) ##开始梯度下降,并且返回每次变化后的x,学习率=η=0.9 cur_x_array = np.array(cur_x_list) cur_y_array = function_1d(cur_x_array) ##绘制曲线图 plt.figure(figsize=(6,4)) plt.subplot() x = cur_x_array y = function_1d(x) plt.plot(x, y, color='b', linewidth=1) ##绘制函数图 x1 = np.arange(-15,15,1) y1 = np.array(function_1d(x1)) plt.plot(x1, y1, color='y', linewidth=1) ##散点图 plt.scatter(cur_x_array,cur_y_array,s=20,c="#ff1212",marker='o') plt.xlabel('梯度下降示例(汽车优化设计)',fontproperties = 'SimHei',fontsize = 10) plt.ylabel('y=(x+1)**2 -1',fontproperties = 'SimHei',fontsize = 10) plt.show() ###输出结果 第0次迭代:x=-12.2 第1次迭代:x=7.960000000000001 第2次迭代:x=-8.168000000000003 第3次迭代:x=4.734400000000003 第4次迭代:x=-5.587520000000003 第5次迭代:x=2.670016000000002 第6次迭代:x=-3.936012800000002 第7次迭代:x=1.3488102400000015 第8次迭代:x=-2.8790481920000017 第9次迭代:x=0.5032385536000015 第10次迭代:x=-2.202590842880001 第11次迭代:x=-0.03792732569599888 第12次迭代:x=-1.769658139443201 第13次迭代:x=-0.3842734884454393 第14次迭代:x=-1.4925812092436486 第15次迭代:x=-0.6059350326050811 第16次迭代:x=-1.3152519739159352 第17次迭代:x=-0.7477984208672518 第18次迭代:x=-1.2017612633061985 第19次迭代:x=-0.8385909893550412 第20次迭代:x=-1.1291272085159672 第21次迭代:x=-0.8966982331872263 第22次迭代:x=-1.082641413450219 第23次迭代:x=-0.9338868692398249 第24次迭代:x=-1.05289050460814 第25次迭代:x=-0.957687596313488 第26次迭代:x=-1.0338499229492095 第27次迭代:x=-0.9729200616406324 第28次迭代:x=-1.021663950687494 第29次迭代:x=-0.9826688394500047 第30次迭代:x=-1.0138649284399963 第31次迭代:x=-0.9889080572480029 第32次迭代:x=-1.0088735542015976 第33次迭代:x=-0.9929011566387219 第34次迭代:x=-1.0056790746890225 第35次迭代:x=-0.995456740248782 第36次迭代:x=-1.0036346078009744 第37次迭代:x=-0.9970923137592205 第38次迭代:x=-1.0023261489926236 第39次迭代:x=-0.9981390808059011 第40次迭代:x=-1.001488735355279 第41次迭代:x=-0.9988090117157767 第42次迭代:x=-1.0009527906273785 第43次迭代:x=-0.9992377674980972 第44次迭代:x=-1.0006097860015222 第45次迭代:x=-0.9995121711987822 第46次迭代:x=-1.0003902630409742 第47次迭代:x=-0.9996877895672206 第48次迭代:x=-1.0002497683462235 第49次迭代:x=-0.9998001853230212 第50次迭代:x=-1.000159851741583 第51次迭代:x=-0.9998721186067335 第52次迭代:x=-1.0001023051146132 第53次迭代:x=-0.9999181559083095 第54次迭代:x=-1.0000654752733524 第55次迭代:x=-0.9999476197813181 第56次迭代:x=-1.0000419041749455 极小值点(-1.0000419041749455,-0.9999999982440401) Process finished with exit code 0
三.求解一个简单的二元函数的极小值


import numpy as np from tqdm import tqdm from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D def plot_3d(): fig = plt.figure(figsize=(12,8)) ax = Axes3D(fig) x = np.arange(-3,3,0.1) y = np.arange(-3,3,0.1) ##对x,y数据执行网格化 x,y = np.meshgrid(x,y) z = -(z1-2*z2)*0.1 ax.plot_surface(x,y,z, rstride=1,##retride(row)指定行的跨度 cstride=1,##retride(column)指定列的跨度 cmap='rainbow') ##设置颜色映射 ##设置z轴范围 ax.set_zlim(-2,2) ##设置标题 plt.title('汽车优化设计之梯度下降--目标函数',fontproperties = 'SimHei',fontsize = 20) plt.show() # plot_3d() '''二维梯度下降法''' def func_2d_single(x,y): ''' 目标函数传入x,y :param x,y: 自变量,一维向量 :return: 因变量,标量 ''' z1 = np.exp(-x**2-y**2) z2 = np.exp(-(x-1)**2-(y-1)**2) z = -(z1-2*z2)*0.5 return z def plot_3d(): fig = plt.figure(figsize=(12,8)) ax = Axes3D(fig) x = np.arange(-3,3,0.1) y = np.arange(-3,3,0.1) ##对x,y数据执行网格化 x,y = np.meshgrid(x,y) z = func_2d_single(x,y) ax.plot_surface(x,y,z, rstride=1,##retride(row)指定行的跨度 cstride=1,##retride(column)指定列的跨度 cmap='rainbow') ##设置颜色映射 ##设置z轴范围 ax.set_zlim(-2,2) ##设置标题 plt.title('汽车优化设计之梯度下降--目标函数3维图',fontproperties = 'SimHei',fontsize = 20) plt.show() plot_3d() def func_2d(xy): ''' 目标函数传入xy组成的数组,如[x1,y1] :param xy: 自变量,二维向量 (x,y) :return: 因变量,标量 ''' z1 = np.exp(-xy[0]**2-xy[1]**2) z2 = np.exp(-(xy[0]-1)**2-(xy[1]-1)**2) z = -(z1-2*z2)*0.5 return z def grad_2d(xy): ''' 目标函数的梯度 :param xy: 自变量,二维向量 :return: 因变量,二维向量 (分别求偏导数,组成数组返回) ''' grad_x = 2*xy[0]*(np.exp(-(xy[0]**2+xy[1]**2))) grad_y = 2*xy[1]*(np.exp(-(xy[0]**2+xy[1]**2))) return np.array([grad_x,grad_y]) def gradient_descent_2d(grad, cur_xy=np.array([1, 1]), learning_rate=0.001, precision=0.001, max_iters=100000000): ''' 二维目标函数的梯度下降法 :param grad: 目标函数的梯度 :param cur_xy: 当前的x和y值 :param learning_rate: 学习率 :param precision: 收敛精度 :param max_iters: 最大迭代次数 :return: 返回极小值 ''' print(f"{cur_xy} 作为初始值开始的迭代......") x_cur_list = [] y_cur_list = [] for i in tqdm(range(max_iters)): grad_cur = grad(cur_xy) ##创建两个列表,用于接收变化的x,y x_cur_list.append(cur_xy[0]) y_cur_list.append(cur_xy[1]) if np.linalg.norm(grad_cur,ord=2)<precision: ##求范数,ord=2 平方和开根 break ###当梯度接近于0时,视为收敛 cur_xy = cur_xy-grad_cur*learning_rate x_cur_list.append(cur_xy[0]) y_cur_list.append(cur_xy[1]) print('第%s次迭代:x,y = %s'%(i,cur_xy)) print('极小值 x,y = %s '%cur_xy) return (x_cur_list,y_cur_list) if __name__=="__main__": current_xy_list = gradient_descent_2d(grad_2d) fig = plt.figure(figsize=(12,8)) ax = Axes3D(fig) a = np.array(current_xy_list[0]) b = np.array(current_xy_list[1]) c = func_2d_single(a,b) ax.scatter(a,b,c,c='Black',s=10,alpha=1,marker='o') x = np.arange(-2,2,0.05) y = np.arange(-2,2,0.05) ##对x,y数据执行网格化 x,y = np.meshgrid(x,y) z = func_2d_single(x,y) ax.plot_surface(x,y,z, rstride=1,##retride(row)指定行的跨度 cstride=1,##retride(column)指定列的跨度 cmap='rainbow', alpha=0.3 ) ##设置颜色映射 # ax.plot_wireframe(x,y,z,) ##设置z轴范围 ax.set_zlim(-2,2) ##设置标题 plt.title('汽车优化设计之梯度下降--二元函数',fontproperties = 'SimHei',fontsize = 20) plt.xlabel('x',fontproperties = 'SimHei',fontsize = 20) plt.ylabel('y', fontproperties='SimHei', fontsize=20) plt.show()
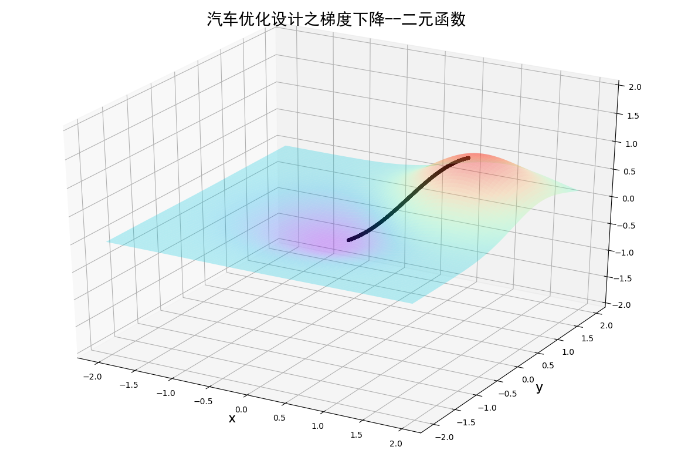
四.梯度下降法在BP神经网络中的实现过程(手动+Excel处理)
BP神经网络中的正向传播和反向传播过程。反向传播中的权重更新,就是通过梯度下降法实现的,损失函数最小化,实质也是一个最优化问题的求解。



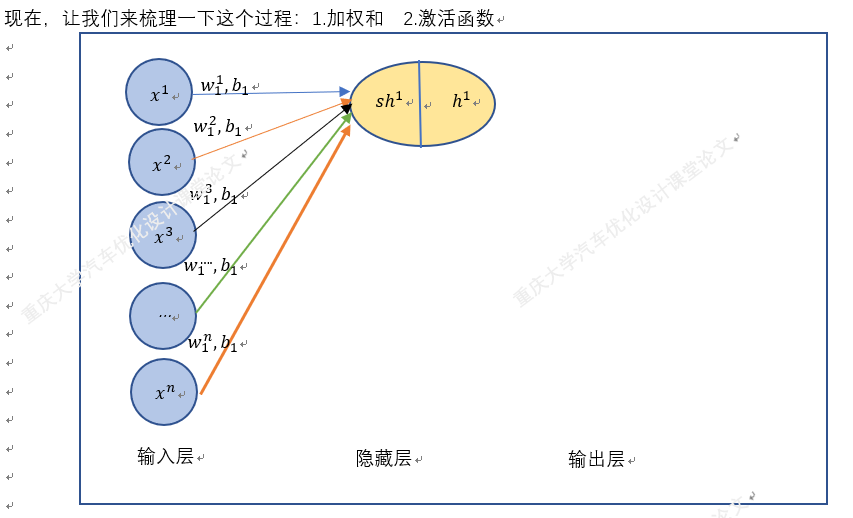

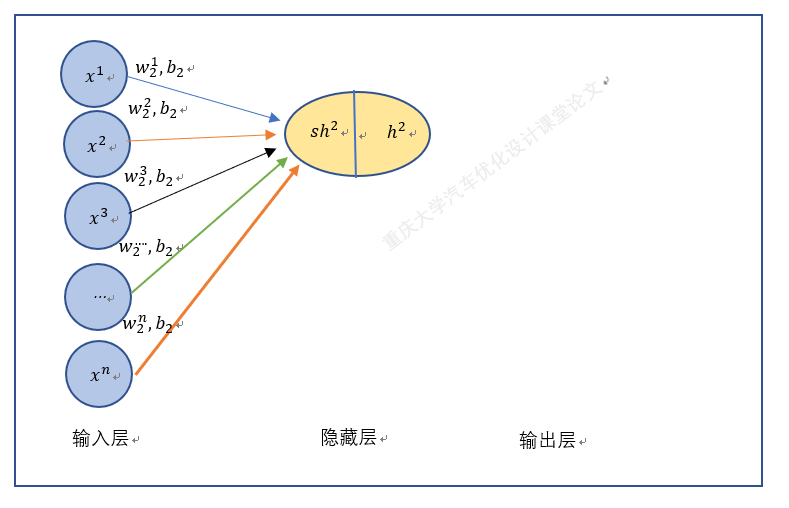

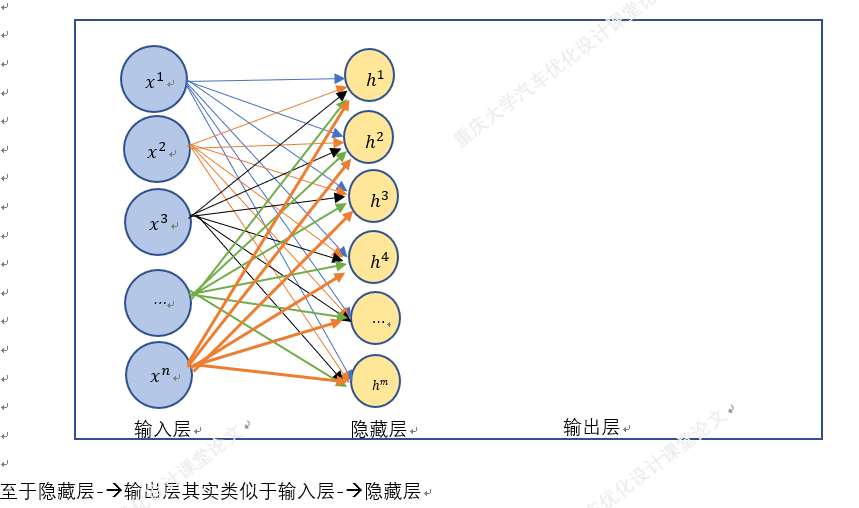
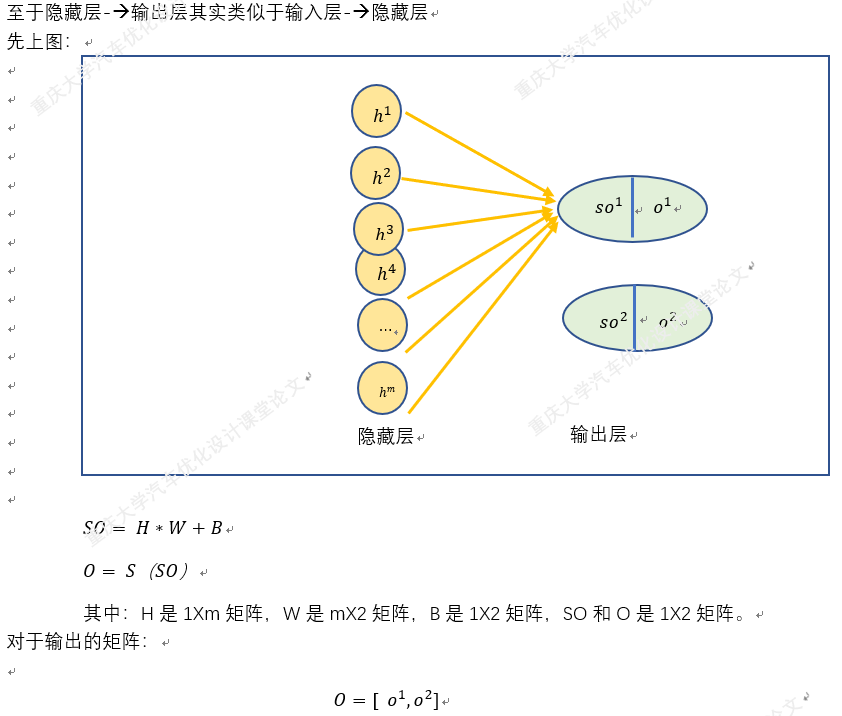

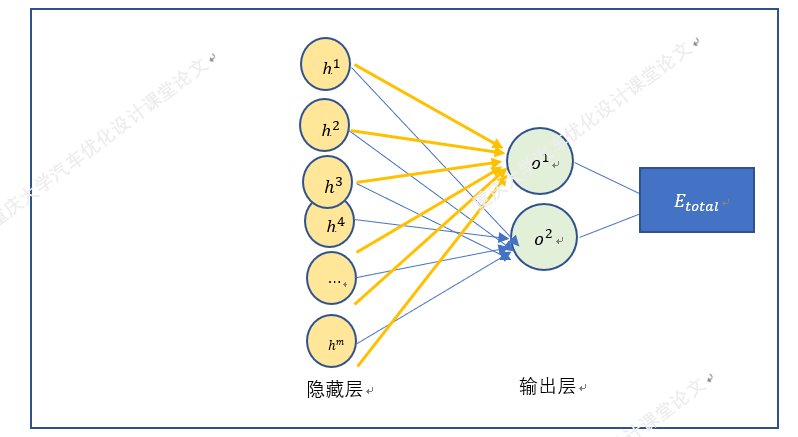


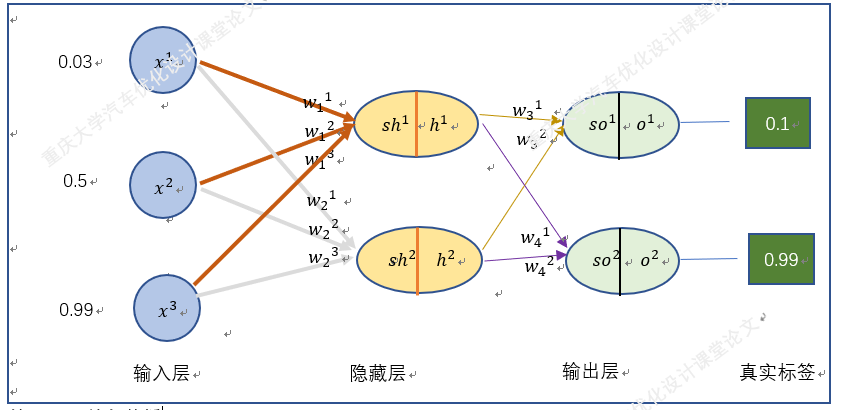


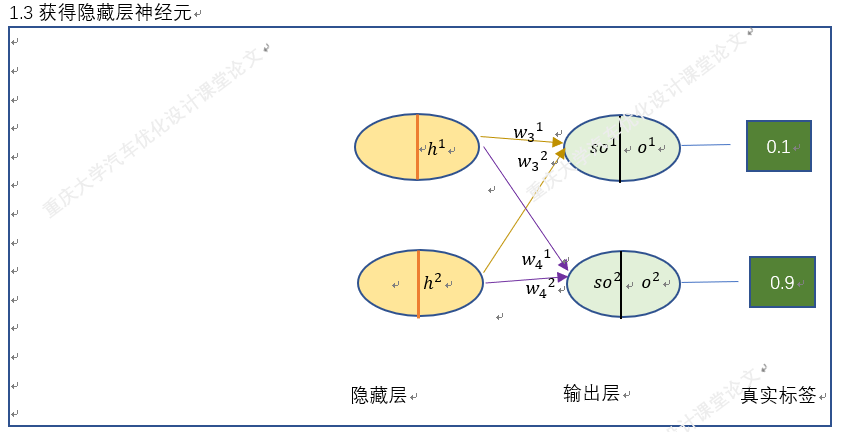


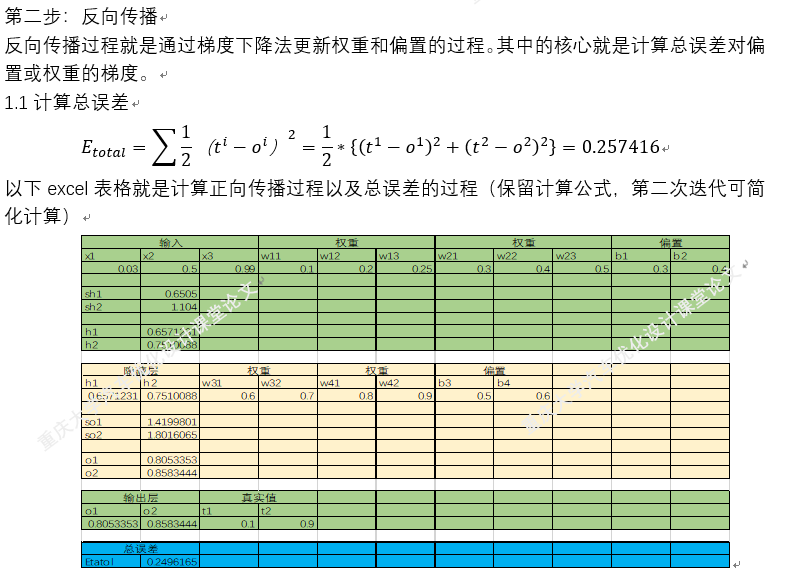



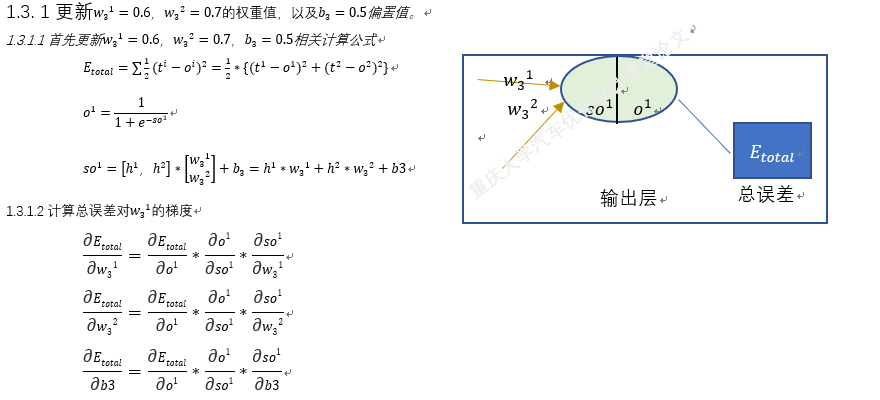



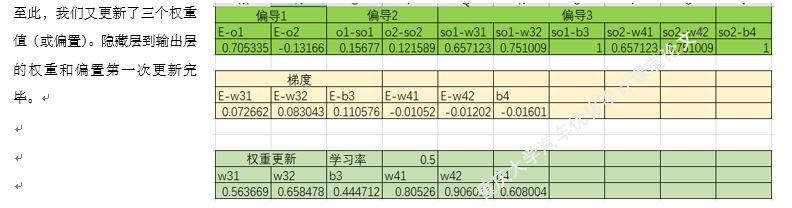

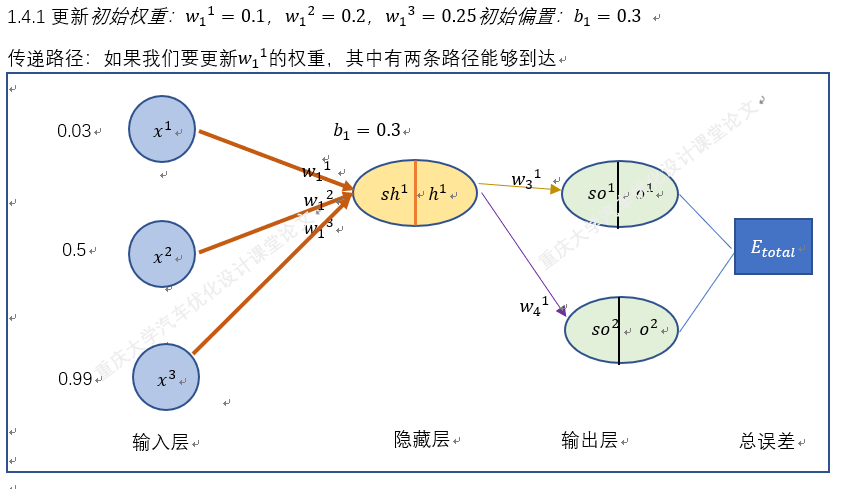


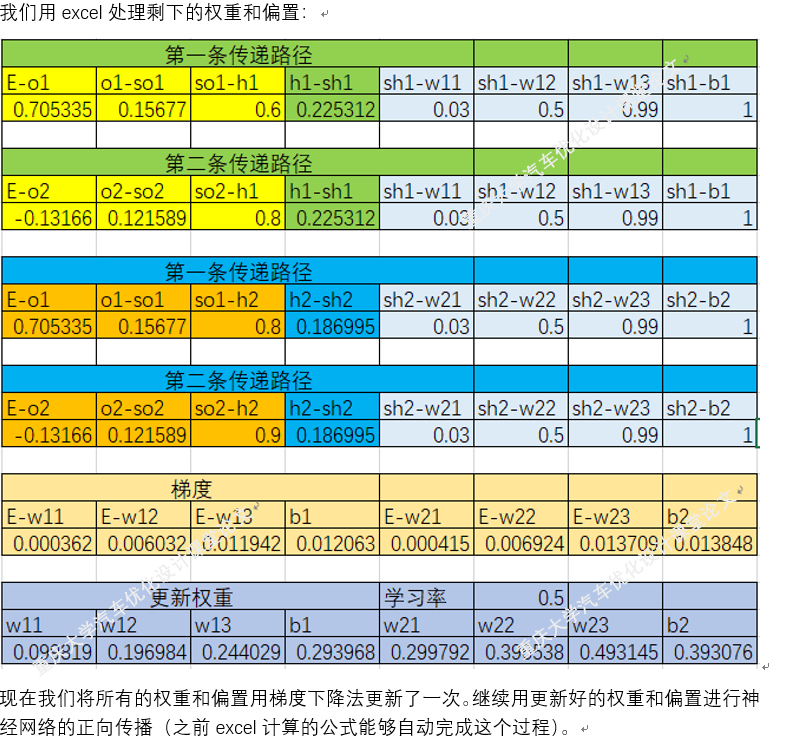

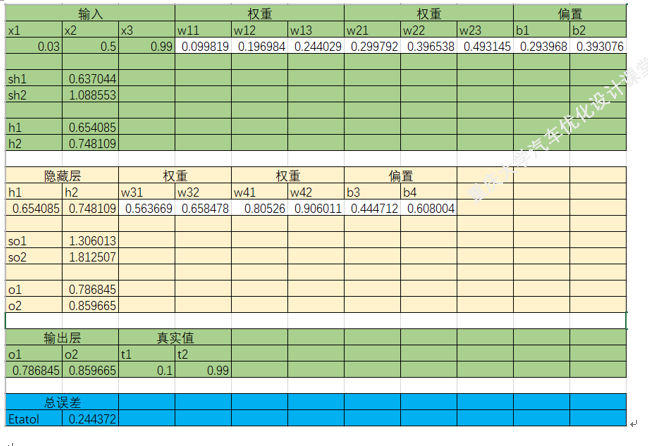
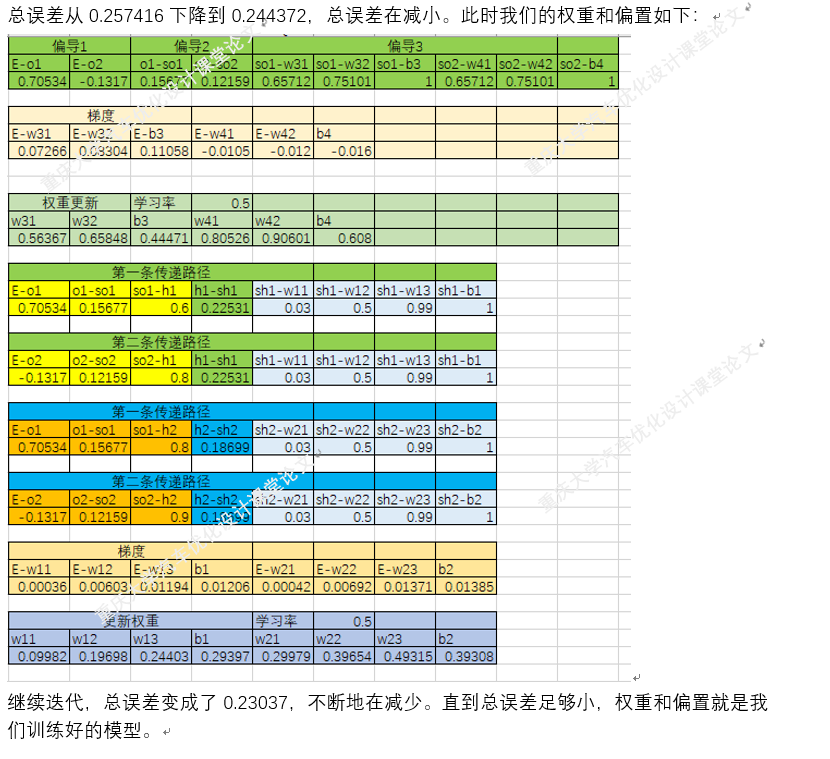
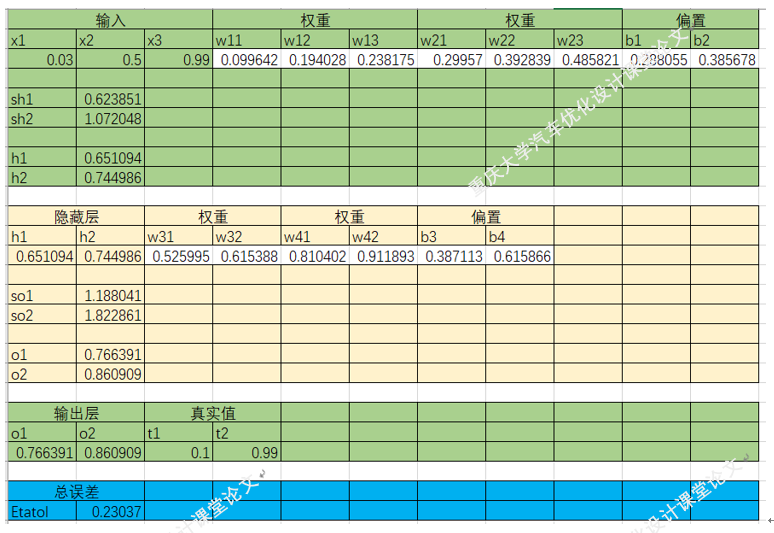
以上就是BP神经网络的实现过程,手动+excel码字只是为了深刻理解神经网络,但这个并没有太大的实质性意义,因为这个已经是成熟的算法。
五.Tensorflow中实现简单的线性回归
深度学习大致分为四个步骤:
1.数据准备
2.模型搭建
3.迭代训练
4.使用模型

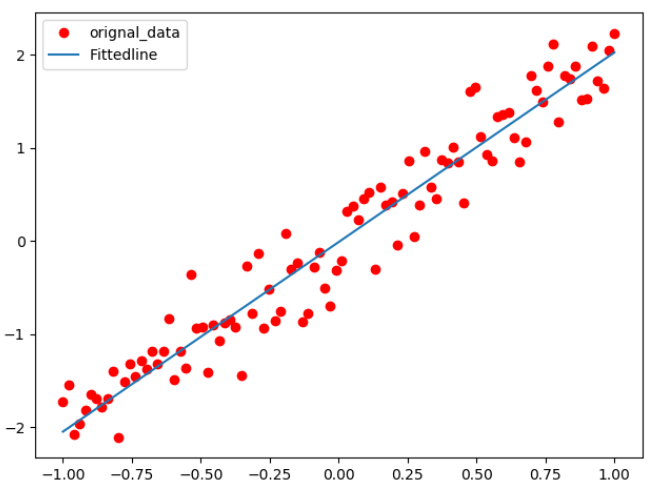
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt ''' 说明:本实例来源于李金洪的《深度学习之Tensorflow入门、原理与进阶实战》机械工业出版社 ''' ##一.数据准备 train_x = np.linspace(-1,1,100) train_y = 2*train_x+np.random.randn(*train_x.shape)*0.3 ###y=2*x 但是加入了噪声 ##显示模拟数据 plt.plot(train_x,train_y,'ro',label='original_data') plt.legend() plt.show()
通过函数y≈2x模拟输入数据。简单来说就是通过y=2x+随机数
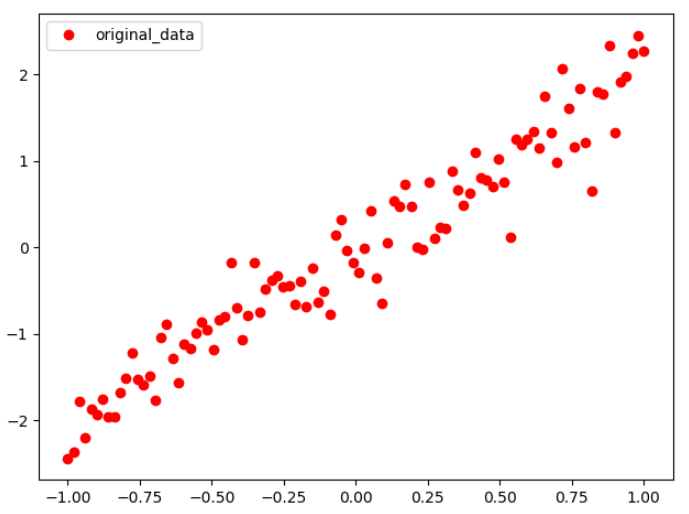
5.2模型搭建

#占位符,状态变量 X= tf.placeholder('float') Y = tf.placeholder('float') ##模型参数,权重和偏置 W= tf.Variable(tf.random_normal([1]),name='weight') b = tf.Variable(tf.zeros([1]),name='bias') ##前向传播结构 z = tf.multiply(X,W)+b
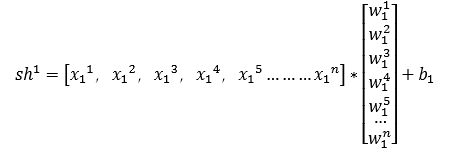

##2.2 反向传播 cost = tf.reduce_mean(tf.square(Y-z)) ##总误差,生成值与真实值的平方差 learning = 0.01 ##学习率 optimizer = tf.train.GradientDescentOptimizer(learning).minimize(cost) ##总误差最小化(封装好的梯度下降法)

##2.3训练模型 #2.3.1初始化所有变量 init = tf.global_variables_initializer() ###权重和偏置等需要给原始值 #2.3.2定义参数 training_epochs = 20 display_step = 2 ##2.3.3启动Session with tf.Session() as sess: sess.run(init) plotdata={'batchsize':[],'loss':[]} ##存放批次值和损失值 ##向模型输入数据 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): sess.run(optimizer,feed_dict={X:x,Y:y}) #显示训练的详细信息 if epoch % display_step ==0: loss = sess.run(cost,feed_dict={X:train_x,Y:train_y}) print("Epoch",epoch+1,'cost=',loss,'W=',sess.run(W),'b=',sess.run(b)) if not (loss =="NA"): plotdata["batchsize"].append(epoch) plotdata["loss"].append(loss) print('Finished!') print("cost=",sess.run(cost,feed_dict={X:train_x,Y:train_y}),"W=",sess.run(W),"b=",sess.run(b)) ###输出结果 ''' Epoch 1 cost= 1.9869132 W= [-0.0750566] b= [0.6703366] Epoch 3 cost= 0.2619767 W= [1.4768808] b= [0.26081827] Epoch 5 cost= 0.12644665 W= [1.8984009] b= [0.10219257] Epoch 7 cost= 0.119223535 W= [2.0077329] b= [0.06028967] Epoch 9 cost= 0.11925003 W= [2.0360081] b= [0.04944004] Epoch 11 cost= 0.119383685 W= [2.0433202] b= [0.04663405] Epoch 13 cost= 0.11942672 W= [2.0452104] b= [0.04590876] Epoch 15 cost= 0.1194384 W= [2.045699] b= [0.04572121] Epoch 17 cost= 0.11944149 W= [2.045826] b= [0.04567254] Epoch 19 cost= 0.119442314 W= [2.0458593] b= [0.04565972] Finished! cost= 0.11944243 W= [2.045865] b= [0.04565755] '''

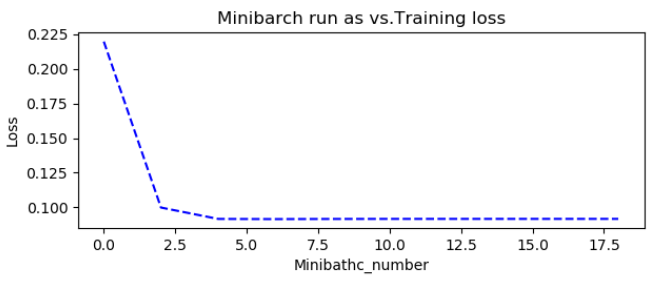
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt ''' 说明:本实例来源于李金洪的《深度学习之Tensorflow入门、原理与进阶实战》机械工业出版社 ''' plotdata = {"batchsize":[],"loss":[]} def moving_average(a,w=10): if len(a)<w: return a[:] return [val if idx<w else sum(a[(idx-w):idx])/w for idx,val in enumerate(a)] ##一.数据准备 train_x = np.linspace(-1,1,100) train_y = 2*train_x+np.random.randn(*train_x.shape)*0.3 ###y=2*x 但是加入了噪声 ##显示模拟数据 plt.plot(train_x,train_y,'ro',label='original_data') plt.legend() plt.show() ##二.模型搭建 ##2.1正向传播 #占位符,状态变量 X= tf.placeholder('float') Y = tf.placeholder('float') ##模型参数,权重和偏置 W= tf.Variable(tf.random_normal([1]),name='weight') b = tf.Variable(tf.zeros([1]),name='bias') ##前向传播结构 z = tf.multiply(X,W)+b ##2.2 反向传播 cost = tf.reduce_mean(tf.square(Y-z)) ##总误差,生成值与真实值的平方差 learning = 0.01 ##学习率 optimizer = tf.train.GradientDescentOptimizer(learning).minimize(cost) ##总误差最小化(封装好的梯度下降法) ##2.3训练模型 #2.3.1初始化所有变量 init = tf.global_variables_initializer() ###权重和偏置等需要给原始值 #2.3.2定义参数 training_epochs = 20 display_step = 2 ##2.3.3启动Session with tf.Session() as sess: sess.run(init) plotdata={'batchsize':[],'loss':[]} ##存放批次值和损失值 ##向模型输入数据 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): sess.run(optimizer,feed_dict={X:x,Y:y}) #显示训练的详细信息 if epoch % display_step ==0: loss = sess.run(cost,feed_dict={X:train_x,Y:train_y}) print("Epoch",epoch+1,'cost=',loss,'W=',sess.run(W),'b=',sess.run(b)) if not (loss =="NA"): plotdata["batchsize"].append(epoch) plotdata["loss"].append(loss) print('Finished!') print("cost=",sess.run(cost,feed_dict={X:train_x,Y:train_y}),"W=",sess.run(W),"b=",sess.run(b)) ###输出结果 ''' Epoch 1 cost= 1.9869132 W= [-0.0750566] b= [0.6703366] Epoch 3 cost= 0.2619767 W= [1.4768808] b= [0.26081827] Epoch 5 cost= 0.12644665 W= [1.8984009] b= [0.10219257] Epoch 7 cost= 0.119223535 W= [2.0077329] b= [0.06028967] Epoch 9 cost= 0.11925003 W= [2.0360081] b= [0.04944004] Epoch 11 cost= 0.119383685 W= [2.0433202] b= [0.04663405] Epoch 13 cost= 0.11942672 W= [2.0452104] b= [0.04590876] Epoch 15 cost= 0.1194384 W= [2.045699] b= [0.04572121] Epoch 17 cost= 0.11944149 W= [2.045826] b= [0.04567254] Epoch 19 cost= 0.119442314 W= [2.0458593] b= [0.04565972] Finished! cost= 0.11944243 W= [2.045865] b= [0.04565755] ''' ##2.3.4训练模型可视化 plt.plot(train_x,train_y,'ro',label='orignal_data') plt.plot(train_x,sess.run(W)*train_x+sess.run(b),label='Fittedline') plt.legend() plt.show() plotdata["avgloss"] = moving_average(plotdata["loss"]) plt.figure(1) plt.subplot(211) plt.plot(plotdata["batchsize"],plotdata["avgloss"],'b--') plt.xlabel('Minibathc_number') plt.ylabel('Loss') plt.title('Minibarch run as vs.Training loss') plt.show()

import tensorflow as tf import numpy as np import matplotlib.pyplot as plt ''' 说明:本实例来源于李金洪的《深度学习之Tensorflow入门、原理与进阶实战》机械工业出版社 ''' plotdata = {"batchsize":[],"loss":[]} def moving_average(a,w=10): if len(a)<w: return a[:] return [val if idx<w else sum(a[(idx-w):idx])/w for idx,val in enumerate(a)] ##一.数据准备 train_x = np.linspace(-1,1,100) train_y = 2*train_x+np.random.randn(*train_x.shape)*0.3 ###y=2*x 但是加入了噪声 ##显示模拟数据 plt.plot(train_x,train_y,'ro',label='original_data') plt.legend() plt.show() ##二.模型搭建 ##2.1正向传播 #占位符,状态变量 X= tf.placeholder('float') Y = tf.placeholder('float') ##模型参数,权重和偏置 W= tf.Variable(tf.random_normal([1]),name='weight') b = tf.Variable(tf.zeros([1]),name='bias') ##前向传播结构 z = tf.multiply(X,W)+b ##2.2 反向传播 cost = tf.reduce_mean(tf.square(Y-z)) ##总误差,生成值与真实值的平方差 learning = 0.01 ##学习率 optimizer = tf.train.GradientDescentOptimizer(learning).minimize(cost) ##总误差最小化(封装好的梯度下降法) ##2.3训练模型 #2.3.1初始化所有变量 init = tf.global_variables_initializer() ###权重和偏置等需要给原始值 #2.3.2定义参数 training_epochs = 20 display_step = 2 ##2.3.3启动Session with tf.Session() as sess: sess.run(init) plotdata={'batchsize':[],'loss':[]} ##存放批次值和损失值 ##向模型输入数据 for epoch in range(training_epochs): for (x,y) in zip(train_x,train_y): sess.run(optimizer,feed_dict={X:x,Y:y}) #显示训练的详细信息 if epoch % display_step ==0: loss = sess.run(cost,feed_dict={X:train_x,Y:train_y}) print("Epoch",epoch+1,'cost=',loss,'W=',sess.run(W),'b=',sess.run(b)) if not (loss =="NA"): plotdata["batchsize"].append(epoch) plotdata["loss"].append(loss) print('Finished!') print("cost=",sess.run(cost,feed_dict={X:train_x,Y:train_y}),"W=",sess.run(W),"b=",sess.run(b)) ###输出结果 ''' Epoch 1 cost= 1.9869132 W= [-0.0750566] b= [0.6703366] Epoch 3 cost= 0.2619767 W= [1.4768808] b= [0.26081827] Epoch 5 cost= 0.12644665 W= [1.8984009] b= [0.10219257] Epoch 7 cost= 0.119223535 W= [2.0077329] b= [0.06028967] Epoch 9 cost= 0.11925003 W= [2.0360081] b= [0.04944004] Epoch 11 cost= 0.119383685 W= [2.0433202] b= [0.04663405] Epoch 13 cost= 0.11942672 W= [2.0452104] b= [0.04590876] Epoch 15 cost= 0.1194384 W= [2.045699] b= [0.04572121] Epoch 17 cost= 0.11944149 W= [2.045826] b= [0.04567254] Epoch 19 cost= 0.119442314 W= [2.0458593] b= [0.04565972] Finished! cost= 0.11944243 W= [2.045865] b= [0.04565755] ''' ##2.3.4训练模型可视化 plt.plot(train_x,train_y,'ro',label='orignal_data') plt.plot(train_x,sess.run(W)*train_x+sess.run(b),label='Fittedline') plt.legend() plt.show() plotdata["avgloss"] = moving_average(plotdata["loss"]) plt.figure(1) plt.subplot(211) plt.plot(plotdata["batchsize"],plotdata["avgloss"],'b--') plt.xlabel('Minibathc_number') plt.ylabel('Loss') plt.title('Minibarch run as vs.Training loss') plt.show() ##3.运用训练好的模型预测 print("x = 0.2,z=",sess.run(z,feed_dict={X:0.2})) print("x = 2,z=", sess.run(z, feed_dict={X: 2})) ''' 预测结果: x = 0.2,z= [0.4100724] x = 2,z= [4.0627713] '''