博文中例子来自于 http://www.cnblogs.com/yjiyjige/p/3263858.html
算法的来历就不仔细说明了,是相对于暴力破解匹配算法来的,其思路如下图

从以上思路可以看出,当被匹配串从k开始比起一直比较到位置i,模式串到了j ,匹配失败了,i向后移动到 k+1的位置 , j 移到0。
而KMP算法改善了暴力破解的效率,其基本思路在是:可以根据模式串的组成规则,从而基本只要移动 j的位置 (当第一个就不匹配的时候,i 也会向后移动一个位置),其思路用图片描述如下
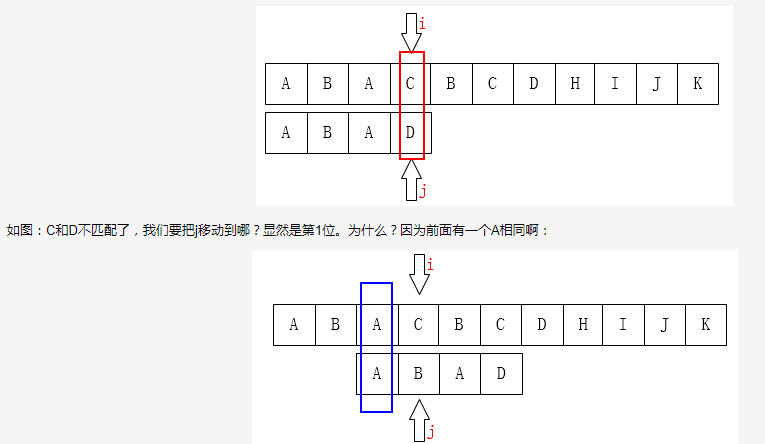
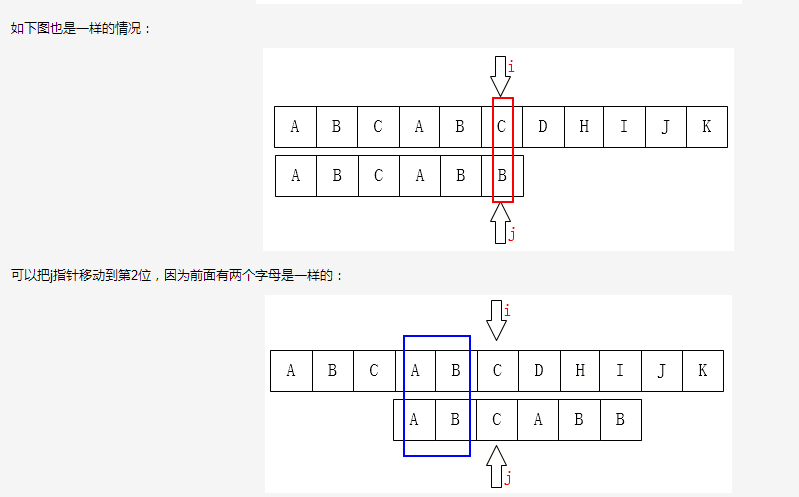
接下来,算法的关键部分就是要根据模式串的组成规则,计算出模式串每个位置 j 移动的next(k)值(即当匹配到模式串位置 j 匹配失败的时候,j 应该回溯到的位置)
public int[] getNext2(String ps) { char[] strKey = ps.toCharArray(); int[] next = new int[strKey.length]; // 初始条件 int j = 0; int k = -1; next[0] = -1; // 根据已知的前j位推测第j+1位 while (j < strKey.length - 1) { if (k == -1 || strKey[j] == strKey[k]) { next[++j] = ++k; // ----> j++ ; k++ next[j] = k; 由此也可以看出求得是第j+1位的next } else { // 例子: //index: 0 1 2 3 4 5 6 7 8 //strKey: a b a d a b a s s //next: -1 0 0 1 0 1 2 3 0 // 当strKey[3]和strKey[7]比较的时候,不相等,这时候应该比较 strKey[next[3]](next[3]=1)和strKey[7],可以看出 // 当strKey[3]、strKey[7]和 strKey[next[3]]前面那个元素都是相同的,都为a。由于strKey[1]=b!=s,所以继续是比较next[1]=0,再进一步变成-1进入判断 // 所以这一步可以理解为 X={a b a d}已经不可能成为模式串 (0~8-1)位的真子集,这时候,可以继续在X中寻找真子集,可能满足要求,若将 strKey[7]改成b,即: //index: 0 1 2 3 4 5 6 7 8 //strKey: a b a d a b a b s //next: -1 0 0 1 0 1 2 3 2 //next[8]最终的结果就为1了 k = next[k]; } } return next; }
这种求next的方法是有缺陷的,若模式从都是sssssssssssb这样的字符串,next = [-1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] ,b之前的任何一个s不匹配完全没有必要再移动模式串 j 的位置,移动后必须是不匹配的
发生问题的原因在于strKey[j] == strKey[ next[j] ]。 该串的next优化后为 [-1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, 10] (负数表现被匹配串 i 后移)

(1) strKey[j] == strKey[ next[j] ] 当 strKey[j] 不匹配时,决定不能在移动到next[j] ,在next[j] 必然失匹配 C != B
主串 A B A C B C D H
strKey A B A B
next -1 0 0 1
(2) strKey[j] != strKey[ next[j] ] 当 strKey[j] 不匹配时,移动在next[j] ,但不一定在next[j] 就会匹配 C != B
主串 A B A C B C D H
strKey A B A D
next -1 0 0 1
(3 当 strKey[j] 不匹配时,只有strKey[j] != strKey[ next[j] ] ,主串才可能匹配 B == B
主串 A B A B A C
strKey A B A C
next -1 0 0 1
所以要过滤掉 strKey[ j ] == strKey[ next[j] ] 的情况,得到以下的第二种算法
public int[] getNext3(String ps) { char[] strKey = ps.toCharArray(); int[] next = new int[strKey.length]; // 初始条件 int j = 0; int k = -1; next[0] = -1; // 根据已知的前j位推测第j+1位 while (j < strKey.length - 1) { if (k == -1 || strKey[j] == strKey[k]) { // 如果str[j + 1] == str[k + 1],回退后仍然失配,所以要继续回退 if (strKey[j + 1] == strKey[k + 1]) { next[++j] = next[++k]; } else { next[++j] = ++k; } } else { k = next[k]; } } return next; }
接下来贴上完整kmp算法
private int kmpMatch(String str , String pattern ){ int next[] = getNext3(str); int i=0,j=0; char[] strChar = str.toCharArray(); char[] patternChar = pattern.toCharArray(); while(i<str.length()&&j<pattern.length()){ if(strChar[i] == patternChar[j]){ i++; j++; }else{ if(next[j]>=0){ j = next[j]; }else{ // 当next[j]<0 即 j为-1,这时j要移动到0的位置,i要往后移动一位,这部分代码可以和上面的合并 i++; j = 0; } } } if( j ==pattern.length()){ return i-j; }else{ return -1; } }