Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in place.
Did you use extra space?
A straight forward solution using O(mn) space is probably a bad idea.
A simple improvement uses O(m + n) space, but still not the best solution.
Could you devise a constant space solution?
【题目分析】
给定一个矩阵,如果矩阵中的某个值为0,那么把矩阵中这个值所在的行和列的元素都设置为0,要求使用固定的空间复杂度。
【思路】
能否不用额外空间做,用常数空间?
这个时候应该有一个意识,遇到数组、矩阵的数据,还要求常数空间的,尽量尝试在数组和矩阵中保存中间结果来实现。
本题也不例外!
怎么保存?
可以从题目要求着手分析。不管在哪个位置遇到了0, 该行该列的其他数字,最终都没有任何意义,因为最终都要被置为0。那么我们可否在该行该列找一个位置用来做个mark呢?
那么,最简单的mark位置,就是第一行第一列嘛。 用第一行来保存各个列的mark,用第一列来保存各个行的mark。最终,分别看第一行和第一列的mark把该行该列置为0不就完了么?!
想起来是很清晰简单的,但是实现了一下,试了两个用例就不行了,我们来看看下面的例子。

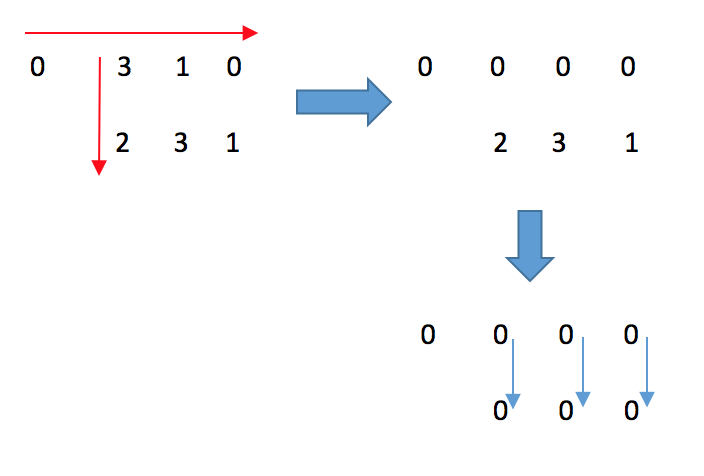
按照上面算法, 在执行完行列mark后,矩阵变为:

那么,按照上面的第一行第一列置位的算法,第一行全部置为0(上方红色箭头), 第一列全部置为0(左边红色箭头),矩阵变为下面:

这显然是错误的,因为第一行除了第一个位置外,其他位置不应该置为0.
问题出在哪里?
应该能看到,问题出在了第一行第一列。因为我们用第一行存储各列的置位情况,用第一列存储各行的置位情况。那么第一行第一列岂不身兼两职?
所以,我考虑引入一个int extra位,单独用来做第一行的置位,而让第一行第一列位置只作第一列的置位情况,这样就把职责区分开了,看下图
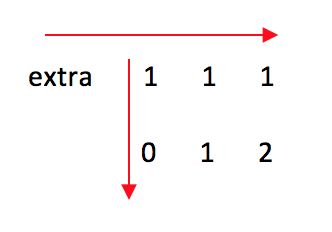
当第一行中有零的时候,extra置为0,作为第一行的mark, 而[0][0]位置作为第一列的mark。那么在mark循环执行完后,矩阵变为上面的样子。
到了这里接下来怎么做就一目了然了, 各行各列还是按照mark位是否为0来给各行各列置位。
我们来看下面例子:
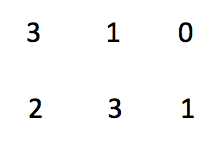
显然, 最终变化应该是第一行和最后一列变为0,其他都保持不变, 我们按照上面的改进算法来走走看:
当走完所有mark流程后,矩阵变为:
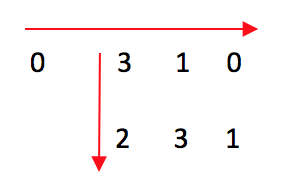
这一步没问题, 接下来,我们对各行各列置位, 首先因为extra负责的是第一行的置位mark, 此时extra==0, 所以第一行全部置位0:
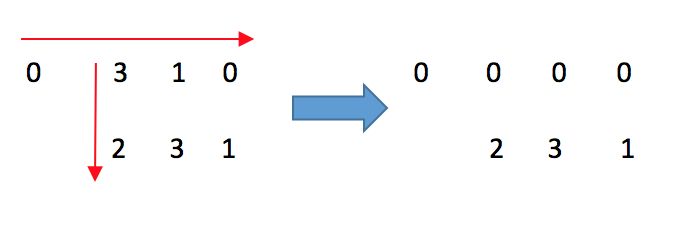
接下来,第二行置位,第二行第一列不是0, 所以本行无需置位。
然后,根据第一行各列对矩阵各个列进行置位,问题来了,根据上面的结果, 这个时候,置位将变为:
这什么情况?!?
显然,原因出在,第一行根据extra置位的时候,我们错误地把[0][0]位也置为0了, 因为[0][0]位其实指示的是第一列的mark,所以[0][0]位不能动!
OK,按行置位改进一下:对第一行第一列不动。其他行算法不变。
这个时候,再根据第一行各个列的情况,对各列置位。
【java代码】
1 public class Solution { 2 public void setZeroes(int[][] matrix) { 3 4 if(matrix == null) return; 5 int row = matrix.length; 6 int col = matrix[0].length; 7 int zerocol = 1;//标记第一列是否需要被设置为0 8 //遍历矩阵,在第一行和第一列中标记哪一行要被设置为0 9 for(int i = 0; i < row; i++){ 10 for(int j = 0; j < col; j++){ 11 if(matrix[i][j] == 0){ 12 if(j == 0){ 13 zerocol = 0; 14 } 15 else{ 16 matrix[i][0] = 0; 17 matrix[0][j] = 0; 18 } 19 } 20 } 21 } 22 //遍历每一列,把需要设置为的0的列设为0 23 for(int j = 1; j < col; j++){ 24 if(matrix[0][j] == 0){ 25 for(int i = 1; i < row; i++) 26 matrix[i][j] = 0; 27 } 28 } 29 //遍历每一行,把需要设置为的0的行设为0 30 for(int i = 0; i < row; i++){ 31 if(matrix[i][0] == 0){ 32 for(int j = 1; j < col; j++) 33 matrix[i][j] = 0; 34 } 35 } 36 //判断第一列是否需要被设为0 37 if(zerocol == 0){ 38 for(int i = 0; i < row; i++) matrix[i][0] = 0; 39 } 40 } 41 }