动态规划入门step-by-step

问题陈述

下面是一道简单的动态规划题目，主要是通过这道题介绍动态规划的一般思考流程。大神请无视。

有连续的n个房子，每个房子有一定的金币。当小偷偷取两个连续的房子时会引发报警，请问这个小偷最多能偷多少金币？

假设有A[1...n]一共n个房子，房子i有A[i]个金币

方法1

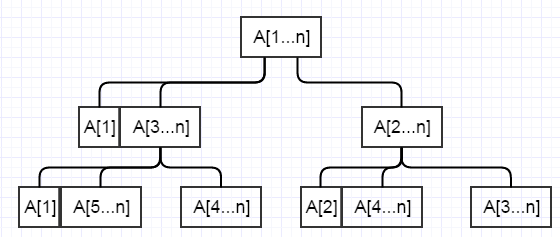
如上图所示。我们首先考虑第一个房子A[1]，如果我们的最优解包含第一个房子A[1]则不包含A[2]，那么最优解就为A[1]+A[3...n];如果不包含A[1]则最优解就在A[2...n]区间内。
即：
最优解：

[S(1,n) = max(A[1] + S(3,n), S(2,n)) ]

根据这个公式写成代码有

def Steal(input, start, end):
    if start == end:
        return input[start]
    elif end - start == 1:
        return max(input[start],input[end])
    else:        
        return max(input[start]+Steal(input,start+2, end), Steal(input, start+1,end))

gold = []
for i in xrange(30):
    gold.append(random.randint(0,10))

start = time.clock()
print Steal(gold, 0, 29)
print 'duration= ',time.clock() - start

可以看到结果为：

方法2

可以看到方法1在递归调用过程中有相同的节点，因此可以采用打表的方法对沿途的节点值进行计算以避免二次计算。

def Steal_mark_table(input, start, end, table):
    if start == end:
        return input[start]
    elif end - start == 1:
        return max(input[start],input[end])
    else:
        temp1 = 0
        temp2 = 0
        if table[start+2]!=0:
            temp1 = table[start+2]
        else:
            temp1 = Steal_mark_table(input,start+2, end, table)
            table[start+2] = temp1
        if table[start+1]!=0:
            temp2 = table[start+1]
        else:
            temp2 = Steal_mark_table(input, start+1,end, table)
            table[start+1] = temp2
        return max(input[start]+temp1, temp2)

gold = []
for i in xrange(30):
    gold.append(random.randint(0,10))

start = time.clock()
mark_table = [0]*30
print Steal_mark_table(gold, 0, 29, mark_table)
print 'duration= ',time.clock() - start
print mark_table

结果为：

可以看到速度得到了极大的提升。

方法3

一般能够使用自顶向下递归表示的动态规划解法都会有自低向上的非递归表示方法。
我们从前向后看

[egin{align} S(1)& = A[1]\ S(1,2)& = max(A[1],A[2])\ S(1,3)& = max(A[1]+A[3], A[2])\ S(1,n)& = max(A[n]+S(1,n-2), S(1,n-1))\ end{align} ]

对应的代码为

def Steal_non_recur(input, start, end):
    table = [0]*len(input)
    table[0] = input[0]
    table[1] = max(input[0], input[1])
    for i in xrange(start+2, end+1):
        table[i] = max(input[i] + table[i-2], table[i-1])
    return table[end]

start = time.clock()
print Steal_non_recur(gold,0,29)
print 'duration= ',time.clock() - start

运行的结果为：

可以看到速度又有了不小的提升。

拓展

如果房子是环形排列的呢？即A[n]之后就是A[1]。
这样我们要分三种情况考虑：

• 既不包含A[n]，也不包含A[1]，即S(2,n-1)

• 包含A[1]但不包含A[n]，即A[1]+S(3,n-1)

• 不包含A[1]但包含A[n],即A[n]+S(2,n-2)

最终结果取这三者最大值即可。