[leetcode]295. Find Median from Data Stream数据流的中位数

Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.

For example,

[2,3,4], the median is 3

[2,3], the median is (2 + 3) / 2 = 2.5

Design a data structure that supports the following two operations:

• void addNum(int num) - Add a integer number from the data stream to the data structure.
• double findMedian() - Return the median of all elements so far.

Example:

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3) 
findMedian() -> 2

题意：

给定一堆数据，求其中位数(将数据升序排列。若数据个数为奇，则正中为中位数；若数据个数为偶，则正中两数平均值为中位数)

---

思路：

显然若数据大，排序再找中位数是不现实的。

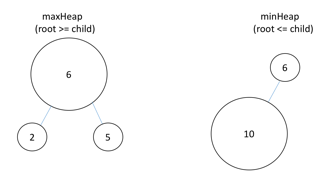
用PriorityQueue分别建maxHeap, minHeap, 并保证maxHeap.size() - minHeap.size() <=1 

如此，当最终maxHeap.size() = minHeap.size()  说明数据个数为偶，取两个Heap的peek值的平均值

         当最终maxHeap.size() > minHeap.size()  说明数据个数为奇，取maxHeap.peek

扫数据中的每个元素

[6,　　10,　　2,　　6,　　5,　　0,　　6,　　3]

  ^  若maxHeap.isEmpty() || 当前元素 < maxHeap.peek() ， 扔到maxHeap里去

[6,　　10,　　2,　　6,　　5,　　0,　　6,　　3]

          ^ 若当前元素 >= maxHeap.peek() ， 扔到minHeap里去

[6,　　10,　　2,　　6,　　5,　　0,　　6,　　3]

                   ^   当前元素 < maxHeap.peek() ， 扔到maxHeap里去

[6,　　10,　　2,　　6,　　5,　　0,　　6,　　3]

                            ^   若当前元素 >= maxHeap.peek() ， 扔到minHeap里去，minHeap会自动将内部最小值sort到peek位置

[6,　　10,　　2,　　6,　　5,　　0,　　6,　　3]

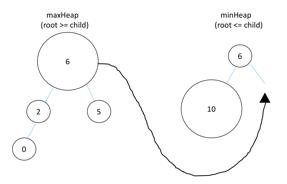
                                     ^   当前元素 < maxHeap.peek() ， 扔到maxHeap里去

此时maxHeap.size() - minHeap.size()  = 2 需要维护平衡

......

如此以往，直至扫完整个数据。

---

 代码：

class MedianFinder {

    /** initialize your data structure here. */
    private PriorityQueue<Integer> _maxHeap; 
    private PriorityQueue<Integer>  _minHeap;

    public MedianFinder() {
        _maxHeap = new  PriorityQueue<> ((o1,o2) -> o2-o1); 
        _minHeap = new  PriorityQueue<> ((o1,o2) -> o1-o2); 
    }
    
    public void addNum(int num) {
        // put each integer into either maxHeap or minHeap
        if(_maxHeap.isEmpty() || num < _maxHeap.peek()){
            _maxHeap.add(num);
        } else{
            _minHeap.add(num);
        }
        // keep balance 
        if(_maxHeap.size() ==_minHeap.size()+2){
            _minHeap.add(_maxHeap.poll());
        }
        
          if(_minHeap.size() ==_maxHeap.size()+1){
            _maxHeap.add(_minHeap.poll());
        }
        
    }
    // the number of data is even or odd 
    public double findMedian() {
        if (_maxHeap.size() == _minHeap.size()) {
            return (_maxHeap.peek() + _minHeap.peek()) /  2.0;
        }else {
            return _maxHeap.peek();
        }
    }       
}

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder obj = new MedianFinder();
 * obj.addNum(num);
 * double param_2 = obj.findMedian();
 */