[leetcode]150. Evaluate Reverse Polish Notation逆波兰表示法

Evaluate the value of an arithmetic expression in Reverse Polish Notation.

Valid operators are +, -, *, /. Each operand may be an integer or another expression.

Note:

• Division between two integers should truncate toward zero.
• The given RPN expression is always valid. That means the expression would always evaluate to a result and there won't be any divide by zero operation.

Example 1:

Input: ["2", "1", "+", "3", "*"]
Output: 9
Explanation: ((2 + 1) * 3) = 9

思路

• 平常我们使用的算式是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
• 逆波兰使用的是运算符写在后面的表达方式，如 1 2 + 3 4 + *  
• 这样写的好处是，在没有括号的情况下不产生歧义

I would use stack to help solving this problem

Traverse the whole given string array 

1. if operand is integer,  push into stack

  

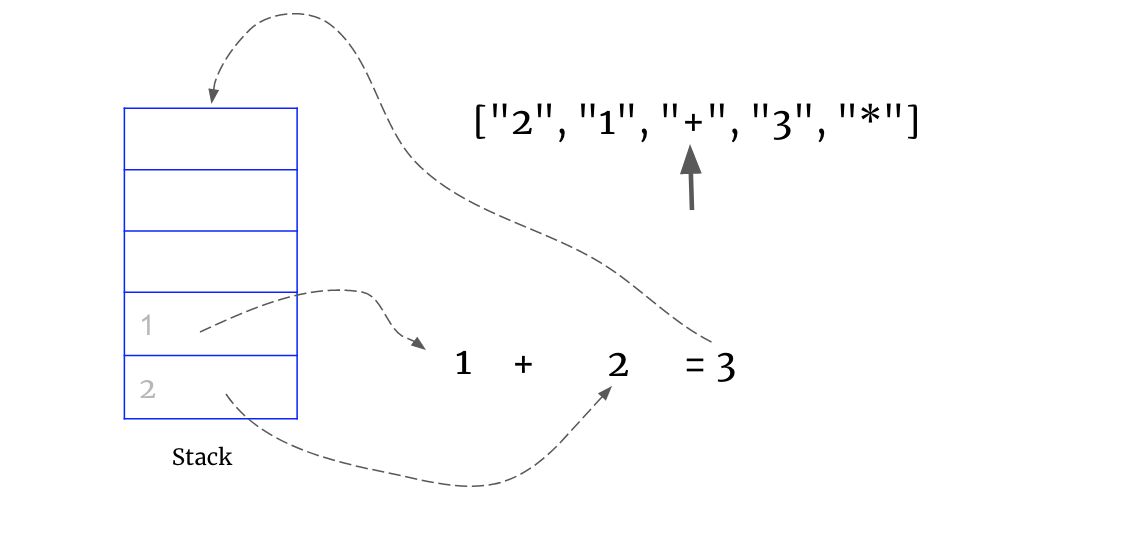
2. if operand is operation, pop two items from stack, do caculation and push result back to stack

code

class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        for (String s : tokens) {
            if(s.equals("+")) {
                stack.push(stack.pop()+stack.pop());
            }else if(s.equals("/")) {
                int latter = stack.pop();
                int former = stack.pop();
                stack.push( former / latter);
            }else if(s.equals("*")) {
                stack.push(stack.pop() * stack.pop());
            }else if(s.equals("-")) {
                int latter = stack.pop();
                int former = stack.pop();
                stack.push(former - latter);
            }else {
                stack.push(Integer.parseInt(s));
            }
        }    
        return stack.pop(); 
    }
}