1.MLE、MAP、Bayesian
首先要明确这三个概念。
MLE是极大似然估计Maximum Likelihood Estimation。其目标为求解:
MAP是最大后验概率Maximum A Posteriori Estimation。其目标是求解:
这两者的区别就是在于求解最优参数时,有没有加入先验知识 (P( heta))。也就是MAP融入了要估计量(θ)的先验分布在其中,因此MAP可以看做规则化的MLE。这也就解释了,为什么MLE比MAP更容易过拟合。因为MLE在求解最优(θ)时,没有对(θ)有先验的指导,因此D中包括了一些outlier的数据样本时,就会很轻易让MLE去拟合outlier样本。而MAP加入了对θ的先验指导,例如L2正则化,那么就不易过拟合了。
举个例子,同样的逻辑回归。
未正则化的逻辑回归就是MLE。
正则化的逻辑回归就是MAP。
那么,与上述两个概念都不同的是贝叶斯模型(Bayesion Model),也被称为概率图模型。这里不是指朴素贝叶斯。而是说下面的这种学习思路。
MLE和MAP求解的都是一个最优的θ值,在预测时只有最优的θ参与预测过程。贝叶斯模型求解的是(θ)的后验分布(P(θ|D)),而不是最大化的后验分布。因此贝叶斯模型在某种程度上可以看作是一个集成模型,在预测时,让所有(θ)都参与预测,并将预测结果以后验概率(P(θ|D))作为权重进行加和作为最终预测值。
2.Why Bayesian?
上面讲述了MLE、MAP和Bayesian的区别,那么为什么要用Bayesian呢?
还举上面逻辑回归的例子,如果是逻辑回归用Bayesian方式来实现,那么训练所得的就是一个后验分布(P(θ|D)),预测时需要用所有(θ)都产生一个预测值,然后用后验分布加权求和。如果(θ)是无穷多的,一般就采样足够的次数,再加权求和。
优势呢?
(1)小数据集时有优势。因为Bayesian的学习方式是一个集成学习的方式,而集成学习在小样本上效果是很好的。不易过拟合。
(2)一种很好地融合参数(θ)先验的方式。例如LDA模型在生成文档时,就对参数做了很多先验假设。
(3)更好地处理不确定性。无论MLE和MAP学习到的参数(θ)都是只有一个,因此预测结果是确定性的。这在很多情况下是不合理的。例如,一个分类模型,永远都会输出分类概率值最大的那一类的标签,但是却不能给出它对这种分类结果有多大的确信度。而Bayesian在给出结果的同时,能够给出对这种结果的模型确信度。如果确信度比较低,那么就可以引入人工干预,这也就是自动驾驶等场景所需要的AI Safety。
3.机器学习中的两种不确定性
(1)偶然不确定性
偶然不确定性是由数据集引入的,而不是模型本身带有的。即数据中的噪音使得数据有了一定bias,进而影响模型预测。
(2)认知不确定性
认知不确定性是由模型引入的,也就是模型遇到完全没有遇到的数据的分布时,就会产生较大的认知不确定性。
而机器学习的预测不确定性是由(1)和(2)共同构成。
举个例子。

M1和M2是没有认知不确定性的。因为对于x属于某个分类的认识,M1和M2模型都给出了确定的判断结果,没有不稳定性。也就是M1和M2是认识x的,就算M2无法分辨x的类属,但是M2是认识x的,只是不知道它的类属而已。M3对x的认识是不稳定的,即有时给出类属1的结果,有时给出类属2的结果,可认为M3模型不认识x。如果是MLE或MAP的模型,那么一定给出的是确定的分类结果,所以体现不出对x的认知不确定性。所以,我们需要用Bayesian模型来表达认知的不确定性。
而预测的不确定性是由认知不确定性和偶然不确定性构成,因此M2和M3都是预测不确定的。因此,Bayesian模型就是希望能够在输出预测值时,将对这个预测值的不确定程度也表达出来。
4.后验分布计算方法
Bayesian的核心就是求解后验分布(P(θ|D)),但是很难求。原因如下:
(P( heta|D)=frac{P(D| heta)P( heta)}{P(D)}) 的分母(P(D))是很难求的。假设(θ)具有 ( heta_1,..., heta_n)共(n)个参数,那么(P(D))的计算如下:
在深度网络中,参数规模上万,那么要积分万次,因此(P(D))难以求解。
而MAP中,求解的是(argmaxP(θ|D))。对于所有的(θ)而言,分母(P(D))是相同的,所以只需要求分子的值就能找出最大的(P(θ|D))。
然而,Bayesian模型要的是后验分布,而不是max,并且直接计算是不可行的,所以就必须采用近似的方法解决后验分布的计算问题。
有两种近似计算方法:
(1)马尔可夫链蒙特卡洛采样
这种方法的本质是对(θ)进行采样。Monte Carlo Sampling 是指对(θ)的多次采样,相互之间是独立的。但是这种采样会效率较低。因为(θ)的采样结果是有启发性的,例如某个(θ)的值对预测结果很好,那么该(θ)值附近的其他(θ)值的质量应该也不错。因此马尔可夫链被引入,即本次采样只受上一次采样结果的影响。例如采样多次,每次采样依赖于前一次采样(θ->θ'->......->θ'''''')。
MCMC的算法有很多。这些采样的方法都是无偏的。最为经典的就是Gibbs Sampling,其实就是coordinate descent思想的应用,即采样一个参数(θ_i)时,固定其他所有参数(θ)。然后再固定(θ_i)和除了(θ_j)的参数,去采样(θ_j)。不断循环,直到收敛。因为Markov Chain是收敛的,所以最后会收敛,证明过程略。只是这个收敛速度不会很快。还有很多其他更快的采样方法,例如对Gibbs Sampling改进的Collapse Gibbs Sampling。
这些算法的具体内容本文不进行介绍。这里只是对MCMC的基本原理介绍一下。
在用Bayesian进行预测时,假设对(θ)采样了(T)次,即( heta_1,..., heta_n)。每个( heta^t)都有(n)维。即模型中的参数共有(n)个。
预测结果本来应该是(int_{ heta}P(y|x)P( heta|D)d heta),即以后验概率(P( heta|D)) 为权重,对各个( heta^{t})预测结果的加和。当(θ)为一个分布时,应该是积分形式。但是问题出在后验概率(P( heta^t|D)) 无法求解,因为每个( heta^t)都有(n)维,无法利用公式
进行求解。
因此,MCMC按照后验概率采样出了一些( heta^1... heta^T)后,预测结果就可以写为如下近似形式:(frac{1}{T}sum_{t=1}^{T}P(y|x; heta^t)),而( heta^t)是服从后验概率(P( heta^t|D))采样得到的。
最后,前面解释了就算用最原始的坐标下降法,也是能够在很多轮的采样后,让预测结果收敛。那么之前未收敛阶段的采样结果就要被丢弃,这个过程称为采样过程中的Burn-in period。即经过了Burn-in period之后的采样值)( heta^t)才会被用于输出预测结果。
(2)变分推断variational inference
与采样方法不同,变分推断属于有偏估计。因为MCMC在采样的数量不断增大的过程中,预测的结果是逐渐与真实情况贴近的。而变分推断是用一个简单的分布去模拟难以求解的后验分布,所以这种简化一定会造成偏差,是有偏估计。
其基本思想就是用简单的分布函数(q(θ))去近似后验概率(P(θ|D))。很多时候用的是meanfield VI,即假设多个(q(θ))是相互独立的。例如:
对于后验分布(P(θ|D)),我们用了三个简单(q)分布去近似,且假设了这些分布是相互独立的。第一和第三个分布是高斯分布,中间的是伯努利分布。
那么现在的问题就是一个寻找(mu_1, sigma_1, mu_2, sigma_2)以及(gamma)的优化问题。即一个分布在已知其形式是高斯还是伯努利的情况下,再知道分布参数,以(mu_1, sigma_1, mu_2, sigma_2)及(gamma)等,那么这个分布就是唯一确定的了。我们的目的就是找到这些能够近似后验分布的简单分布,那就需要确定这些简单分布的形式,并求出分布参数。而简单分布的形式相当于就是我们引入的先验,这就会对估计造成有偏影响。在变分法中,我们只能在预先定义了简单分布的类型后,去求解最优化的分布参数。
那么具体的优化目标如何定义呢?因为衡量两个分布是否近似的最常见的方法就是用KL散度,因此可以从KL散度推导出优化目标函数。
最后一项不含(θ),即对于所有的θ而言,都是相同的,因此在求解最优参数,(mu_1, sigma_1, mu_2, sigma_2)以及(γ)时,可以省略。
于是我们只要最大化括号内的部分(E_q[logP( heta,D)]+E_q[logq( heta)]),就可以让KL散度最小化,即让两个分布最接近。这部分也被称为ELBO。因此,变分推断就变成了对ELBO部分的最大化求解问题了。最终的求解过程,就是一个不断化简的过程,将θ原有参数用新参数,(mu_1, sigma_1, mu_2, sigma_2)以及γ不断替换的过程。此时,再求解最优的(mu_1, sigma_1, mu_2, sigma_2),以及(γ),就可以用坐标下降法来求解了。即固定其他参数,对某个参数求导,令导数为0等,不断循环更新,直到收敛。
5贝叶斯神经网络VS普通神经网络
一图就可以概括了。
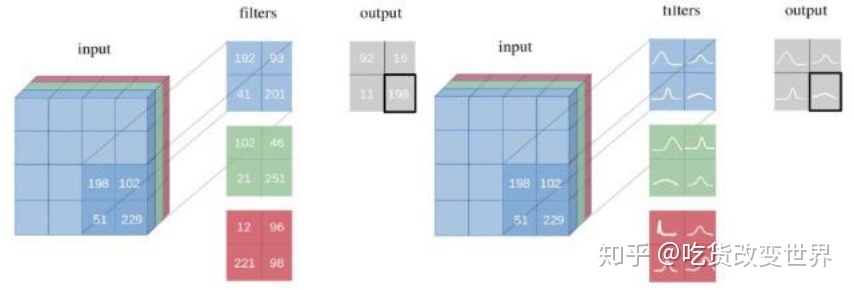
普通神经网络的所有参数都是一个值,网络的预测输出也是一个值。
贝叶斯神经网络的所有参数都是一个分布,网络的预测输出也是一个分布。
从MLE、MAP、Bayesian的角度再来理解一下这个事情。一个普通的神经网络,它做的事情就是最大化地拟合数据样本,也就是所谓的MLE最大似然。如果给这个神经网络中的参数添加一些先验的约束,例如,将先验概率设为权重w符合均值为0,方差为(frac{1}{lambda}I^2) 的高斯分布,则就相当于添加了 (lambda W^TW) 的L2正则化项。也就是对参数正则化后的神经网络可看作是MAP。而不论是MLE还是MAP都是上图的左侧部分。
相比于前两者,贝叶斯方法求解的不是一个极值点,而是要每个参数的整个分布,见上图右侧,所以计算代价是很大的。这也是贝叶斯神经网络应用的一个障碍。
6贝叶斯深度学习的实现方式
前面已经介绍了了贝叶斯神经网络所求解的是每个参数的分布,因此计算量很大,要想构建层数很多的网络是不现实的。
如果层数不多,则可以用Pyro等概率编程工具。基本方法就是给出网络本身的先验定义,然后给出变分推断中的q函数的定义,那么Pyro会自动用变分法求解出近似值的。通常假设的是网络参数都服从高斯分布,然后在输入数据后要学习到一个后验分布。我们需要对这个后验分布进行变分推断的近似。通常也会假设网络参数符合高斯分布(简单分布),然后用这个高斯分布区近似后验分布,优化的loss就是ELBO。最后,就能够得到每个参数所符合的一个合理高斯分布,而这些参数的高斯分布式能够近似出后验分布的。
另一种,贝叶斯深度学习的近似是论文Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning提出的。也就是将采用MC Dropout视为对贝叶斯模型的近似。
其本质是在训练和测试阶段都打开dropout。而MC Dropout相当于下面式子的效果,即让每个参数(W_i)以一定概率有非0值或0值,并让这种选择符合伯努利分布。
上式(M_i)为参数的真实值,而diag对角阵中的对角元素(Z_{ij})服从伯努利分布。
在这种情况下,深度网络开启MC Dropout后,就相当于是在用伯努利分布(简单分布)去近似每个参数的后验分布,这就是变分推断。因此,有MC Dropout的深度网络相当于近似了一个贝叶斯模型的变分推断。与上面提到的用Pyro实现的贝叶斯神经网络的区别仅在于,Dropout是用伯努利分布作为简单分布区近似后验分布,而不是高斯分布而已。
因此,带MC Dropout的网络学到了每个参数的伯努利分布参数p,但是网络的输出还是一个值。为了得到一个分布,就必须在测试的预测阶段(前向传播)中,也要开启Dropout,并运行多次,例如100次,然后对100个结果求均值和方差,形成一个分布。
实验效果如下图:
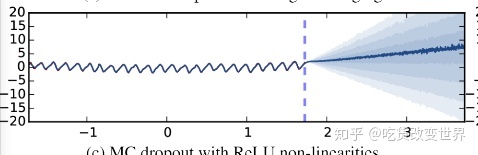
在数据样本集中的区域,预测结果的不确定性是较低的,而在样本稀疏区域,不确定性呈扇形扩大了。这也非常符合现实生活。例如天气预报,总是预测明天的,比预测后天的要有把握。
最后,在样本集较小或imbalance的样本集上,用贝叶斯神经网络的效果要更好,这也变相解释了为什么Dropout对小样本和imbalance样本集有效果的原因。