数据结构-二叉树

一、树的简单介绍

树具有两种数据结构的优点，一种是有序数组，另一种是链表。在树中查找就和在有序数组中查找一样，在树中插入数据和删除数据项的速度也和链表的操作一样。题外话，有序数组的查找一般使用二分法比较快。
有序数组的缺点是，插入数据项比较慢，删除数据项的时间复杂度也是O(n)，查询的时间复杂度为O(log(N))。链表的缺点是：数据的查询太慢，时间复杂度为O(N)，插入和删除数据的复杂度均为O(1)。
树是由边连接的节点组成，也就是说树由边和节点组成，节点又分为叶子节点和非叶子节点。树只有而且仅有一个根节点。

二、树中的常用名字定义
路径：顺着连接节点的边从一个节点走到另外一个节点，所经过多节点顺序排列就被称为“路径”。
根：树顶端的节点被称为“根”。一个树只有一个根。如果要把一个节点和边的集合定义为树，那么从根高其他任何节点都必须有且仅有一条路径。
父节点：每个节点（根节点除外）都恰好有一条边向上连接到另外一个节点，上面这个节点就被称为该节点的父节点。
子节点：每个节点都有可能有一条或者多条向下连接其他节点，而下面这个节点就是叶子节点。
子树：每个节点都可以作为“子树”的根，它以及它所有的子节点，子节点的子节点等都包含在子树中。
访问：当程序控制流程到达某个节点时，就称为“访问”该节点，通常是为了操作该节点，比如查看数据字段或显示节点，如果仅仅是经过，那么不算是访问。
遍历：遍历树意味着要遵循某种特殊访问树中的所有的节点。比较常用的三种遍历方式是：先序遍历，中序遍历，后序遍历。
层：一个节点的层次是指从根开始到这个节点有多少“代”，假设根节点是第0层，那么根节点的直接子节点就是第1层，孙节点就是第2层，一次类推。
关键字：对象中通过会有一个数据域被指定为关键字值。通常用户查询或者其他操作。
二叉树：如果树中每个节点最多只能有两个子节点，那么这中树就被称为“二叉树”。二叉树中，每个节点的两个子节点分别被称为“左子节点”和“右子节点”，当然也可以只有单独的“左子节点”或者“右子节点”，也可以没有子节点。二叉树的结构如图：

二叉搜索树：在一个二叉树中，任意节点A的左子树中的所有节点的关键字的值要小于节点A的关键字的值，右子树的所有节点的关键字的值要大于或者等于节点A的关键字的值。
非平衡树：树的大部分节点在树的一边，一般来形容二叉树。同时也可能存在非平衡子树。二叉搜索树的结构如图：

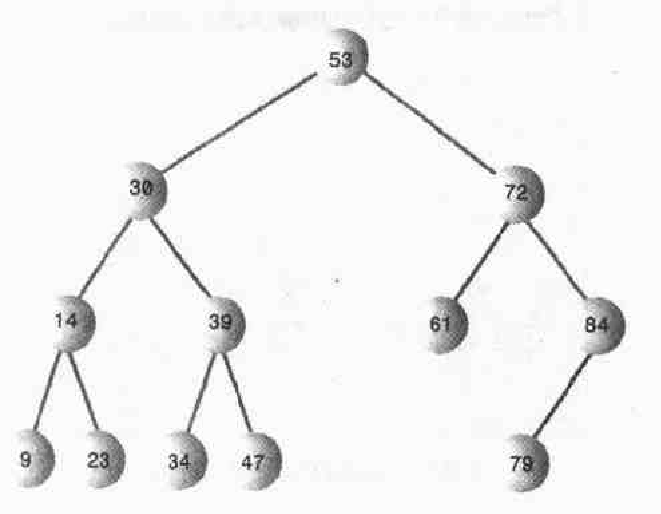
在二叉树中，如果插入的数据是有序的，那么可能会导致二叉树的生产是一个非平衡点二叉树。

三、二叉树的代码实现(JAVA)

首先需要一个节点类Node，这个节点类必须包含数据对象(一个或多个)以及指向子节点的链接。下面就是这个类的描述语句：

public class Node<T> implements java.io.Serializable {

    private static final long serialVersionUID = -1180807550428965783L;
    /**
     * 节点数据对象
     */
    public final T data;
    /**
     * 指向左子树，如果为null，表示没有左子树
     */
    public Node<T> leftNode;
    /**
     * 指向右子树，如果为null，表示没有右子树
     */
    public Node<T> rightNode;

    public Node() {
        this(null);
    }

    public Node(T data) {
        this(data, null, null);
    }

    public Node(T data, Node<T> leftNode, Node<T> rightNode) {
        super();
        this.data = data;
        this.leftNode = leftNode;
        this.rightNode = rightNode;
    }

    @Override
    public String toString() {
        return "[data=" + data + ", leftNode=" + leftNode + ", rightNode=" + rightNode + "]";
    }
}

 除了这种表示方式外，还可以在Node节点中加入指向父节点的链接，这样可以简化一部分操作，但是可能会使删除等其他操作比较复杂。这个的T是一种泛型的表示方式，一般我会将它指向一个自定义的类对象，比如User、Person等。

除了Node节点外，还需要一个表示树本身的类，即Tree。这个类的实例包含所有的节点信息，一般只有一个节点：根的Node对象，其他节点由根目录遍历访问。Tree类主要包括查询、插入、删除节点，进行各种不同的遍历，显示树等操作。Tree类的大体结构如下所示：

public class SBinaryTree<T extends Comparable<T>> {
    private Node<T> root; // 根节点
    public void insert(T data) {
        // TODO: insert the data to tree
    }

    public Node<T> find(T data){
        // TODO: find the data node
        return null;
    }
    public boolean delete(T data) {
        // TODO: delete the data, if the tree has more than one macthed node, delete the first node.
        return false;
    }
    public void display() {
        // TODO: show the tree
    }
    public String preorder() {
        // TODO: 
        return null;
    }

    public String inorder() {
        // TODO:
        return null;
    }
    public String postorder() {
        // TODO:
        return null;
    }
}

 查找节点

查找节点一般是根据二叉搜索树中节点对应信息的对象的比较方法来进行判断的，所以一般Node节点的data数据是一种支持判断的节点类型，这里我们将其看成是Comparable的实现。当然了，也可以指定其他对应的比较方法，这个在这里不做考虑。二叉搜索树的查询时间复杂度为O(log₂N)。

二叉搜索树具有左子树的值小于根节点的值，根节点的值小于或者等于右子树的值，即左子树<根<=右子树。代码实现如下：

/**
 * 在二叉搜索树中查询节点数据为data的节点，如果没有匹配的，那么返回null。
 * 
 * @param data
 * @return
 */
public Node<T> find(T data) {
    Node<T> current = this.root;
    if (data == null) {
        while (current != null && current.data != null) {
            current = current.leftNode;
        }
    } else {
        while (current != null) {
            if (current.data == null) {
                current = current.rightNode;
            } else {
                int t = data.compareTo(current.data);
                if (t == 0) {
                    break;
                } else if (t < 0) {
                    // data < current.data
                    current = current.leftNode;
                } else {
                    current = current.rightNode;
                }
            }
        }
    }
    return current;
}

在整个过程中，将current设置为正在查看的节点，从根节点root开始，如果current节点的data值小于要查询的data值，那么将current指向左子节点，如果大于，那么指向右子节点，如果等于，那么直接返回current，此时的current就是要查找的节点。如果current为null，表示没有找到对应的Node节点。定义：null值是一个最小的值，即比任何其他值都要小。

 插入节点

在二叉搜索树中，插入一个节点的第一步就是要找到一个插入的地方。从根节点开始找到一个相对应的节点，这个就是新节点的父节点，新的节点就可以连接到它的左子节点或者是右子节点上了，这个取决于新节点的值是比父节点的值大还是小。Java实现代码如下：

/**
 * 插入一个节点到树中
 * 
 * @param data
 */
public void insertData(T data) {
    if (root == null) {
        root = new Node<T>(data);
    } else {
        Node<T> parent = null;
        Node<T> current = this.root;

        if (data == null) {
            while (current != null && current.data != null) {
                parent = current;
                current = current.leftNode;
            }
        } else {
            while (current != null) {
                if (current.data == null) {
                    parent = current;
                    current = current.rightNode;
                } else {

                    int t = data.compareTo(current.data);
                    if (t == 0) {
                        break;
                    } else if (t < 0) {
                        // data < current.data
                        parent = current;
                        current = current.leftNode;
                    } else {
                        parent = current;
                        current = current.rightNode;
                    }
                }
            }
        }

        if (current == null) {
            Node<T> newNode = new Node<T>(data);
            if (parent.data == null || (data != null && data.compareTo(parent.data) >= 0)) {
                parent.rightNode = newNode;
            } else {
                parent.leftNode = newNode;
            }
        } else {
            current.rightNode = new Node<T>(data, null, current.rightNode);
        }
    }
}

 遍历树

遍历树的意思就是根据一种特定的顺序访问树的每一个节点，这种技术在理论上是比较有意义的。有三种简单的遍历方法，分别是：前序(preorder)、中序(inorder)、后序(postorder)。遍历操作可以在任何二叉树上进行操作，不仅仅只是二叉搜索树，遍历树不考虑节点的值的大小。

 中序遍历

中序遍历会将二叉搜索树中的所有节点按照关键字的升序被访问到，如果希望创建一个有序的数据类型，那么这个是一种方法。中序遍历的规则是：

1. 初始化当前节点为根节点。
2. 调用方法自身来访问当前节点的左子树
3. 访问这个节点(这个过程可能是，输出到某个文件，打印节点.......)
4. 调用方法自身来访问当前节点的右子树

中序遍历的Java实现的代码如下所示：

/**
 * 中序遍历
 * @return
 */
public String inorder() {
    return this.inorder(this.root);
}

private String inorder(Node<T> node) {
    StringBuffer sb = new StringBuffer();
    if (node != null) {
        sb.append(this.preorder(node.leftNode));
        sb.append(node.data).append(orderSplit);
        sb.append(this.preorder(node.rightNode));
    }
    return sb.toString();
}

使用中序遍历一个三颗节点的树，那么操作的结果如图：

 前序遍历和后序遍历

前序遍历和后序遍历不像中序遍历那样，可以用户排序等地方。但是这两种排序方式我们经常用作表达式的表示方式上。我们在非叶子节点上保持运算符号，在叶子节点上保持数据，比如A,B,C等。

中缀：A*(B+C)

前缀：*A+BC  

后缀：ABC+*  

前序遍历和后序遍历的实现代码是：

/**
 * 前序遍历
 * 
 * @return
 */
public String preorder() {
    return this.preorder(this.root);
}

private String preorder(Node<T> node) {
    StringBuffer sb = new StringBuffer();
    if (node != null) {
        sb.append(node.data).append(orderSplit);
        sb.append(this.preorder(node.leftNode));
        sb.append(this.preorder(node.rightNode));
    }
    return sb.toString();
}

/**
 * 后序遍历
 * @return
 */
public String postorder() {
    return this.postorder(this.root);
}

private String postorder(Node<T> node) {
    StringBuffer sb = new StringBuffer();
    if (node != null) {
        sb.append(this.preorder(node.leftNode));
        sb.append(this.preorder(node.rightNode));
        sb.append(node.data).append(orderSplit);
    }
    return sb.toString();
}

前序遍历的规则是：

1. 初始化当前节点为根节点。
2. 访问这个节点(这个过程可能是，输出到某个文件，打印节点.......)
3. 调用方法自身来访问当前节点的左子树
4. 调用方法自身来访问当前节点的右子树

后序遍历的规则是：

1. 初始化当前节点为根节点。
2. 调用方法自身来访问当前节点的左子树
3. 调用方法自身来访问当前节点的右子树
4. 访问这个节点(这个过程可能是，输出到某个文件，打印节点.......)

 查找最大值和最小值

在二叉搜索树中，查找最大值和最小值是轻而易举的事情，实际上来说，二叉搜索树中，最小值是树的最左子节点的值，最大值是树的最右子节点的值。直接贴代码了，这个就不做多的描述。

/**
 * 寻找最小值节点
 * 
 * @return
 */
public Node<T> findMinDataNode() {
    Node<T> current = this.root;
    while (current != null && current.leftNode != null) {
        current = current.leftNode;
    }
    return current == null ? null : current;
}

/**
 * 寻找最大值节点
 * 
 * @return
 */
public Node<T> findMaxDataNode() {
    Node<T> current = this.root;
    while (current != null && current.rightNode != null) {
        current = current.rightNode;
    }
    return current == null ? null : current;
}

 删除节点 

删除节点是二叉搜索树常用的一般操作中最复杂的，但是，删除节点也是非常重要的一种操作方法。删除节点第一步也是要找到要删除的节点，第二不才是删除操作。一般情况下，删除节点有三种情况需要考虑：

1. 该节点是叶子节点(没有子节点)
2. 该节点有一个子节点
3. 该节点有两个子节点

 情况1：删除一个没有子节点的节点

这种情况下，只需要改变该节点的父节点指向对应的引用指向null即可，要删除的节点还是存在，但已经不是树的一部分了，此时Java语言的垃圾自动收集机制会自动的删除该节点的内存空间，如果是C或者是C++，那么需要手动调用free()或者delete()方法销毁该节点的内存)。Java实现代码如下所示：

/**
 * 删除data，如果有多个数据，值删除第一个
 * 
 * @param data
 * @return
 */
public boolean delete(T data) {
    Node<T> parent = null;
    Node<T> current = this.root;
................
               // 当前节点不是根节点, parent不为null
        if (current.leftNode == null && current.rightNode == null) {
            // 当前节点没有子节点
            if (this.root == current) {
                this.root = null;
            } else {
                if (parent.leftNode == current) {
                    parent.leftNode = null;
                } else {
                    parent.rightNode = null;
                }
            }
        } 
.................

 情况2：删除一个有一个子节点的节点

在这种情况下，只需要将要删除节点的子节点连接到父节点上就可以了，如图：

Java的实现代码是：

// 当前节点有一个子节点
if (this.root == current) {
    this.root = current.leftNode == null ? current.rightNode : current.leftNode;
} else {
    if (parent.leftNode == current) {
        // 要删除的节点是父节点的左子树
        parent.leftNode = current.leftNode == null ? current.rightNode : current.leftNode;
    } else {
        // 要删除的节点是父节点的右子树
        parent.rightNode = current.leftNode == null ? current.rightNode : current.leftNode;
    }
}

 情况3：删除有两个子节点的节点

因为要删除的节点有两个子节点，所以不能够简单用它的子节点代替要删除的节点，但是考虑中序遍历，我们会发现要删除节点的后继节点就是可以替代的子节点，如图：

那么问题就缩减为查询要删除节点的后继节点。那么可以从要删除的节点开始，第一步查找它的右子节点，并设为当前节点。然后继续迭代查找当前节点的左子节点，并令为当前节点，如果左子节点存在的情况下。直到当前节点没有左子节点的时候，结束循环，此时当前节点就是删除节点的后继节点。删除代码如下：

// 当前节点有两个子节点
Node<T> tparent = current;
Node<T> tcurrent = current.rightNode;
while (tcurrent.leftNode != null) {
    tparent = tcurrent;
    tcurrent = tcurrent.leftNode;
}

tcurrent.leftNode = current.leftNode;

if (tparent.leftNode == tcurrent) {
    tparent.leftNode = null;
} else {
    tparent.rightNode = null;
}
if (this.root == current) {
    this.root = tcurrent;
} else {
    if (parent.leftNode == current) {
        parent.leftNode = tcurrent;
    } else {
        parent.rightNode = tcurrent;
    }
}
current.leftNode = current.rightNode = null;

删除节点的全部代码如下所示：

/**
 * 删除data，如果有多个数据，值删除第一个
 * 
 * @param data
 * @return
 */
public boolean delete(T data) {
    Node<T> parent = null;
    Node<T> current = this.root;

    if (data == null) {
        while (current != null && current.data != null) {
            parent = current;
            current = current.leftNode;
        }
    } else {
        while (current != null) {
            if (current.data == null) {
                parent = current;
                current = current.rightNode;
            } else {
                int t = data.compareTo(current.data);
                if (t == 0) {
                    break;
                } else if (t < 0) {
                    // data < current.data
                    parent = current;
                    current = current.leftNode;
                } else {
                    parent = current;
                    current = current.rightNode;
                }
            }
        }
    }

    if (current == null) {
        return false;
    } else {
        // 当前节点不是根节点, parent不为null
        if (current.leftNode == null && current.rightNode == null) {
            // 当前节点没有子节点
            if (this.root == current) {
                this.root = null;
            } else {
                if (parent.leftNode == current) {
                    parent.leftNode = null;
                } else {
                    parent.rightNode = null;
                }
            }
        } else if (current.leftNode != null && current.rightNode != null) {
            // 当前节点有两个子节点
            Node<T> tparent = current;
            Node<T> tcurrent = current.rightNode;
            while (tcurrent.leftNode != null) {
                tparent = tcurrent;
                tcurrent = tcurrent.leftNode;
            }

            tcurrent.leftNode = current.leftNode;

            if (tparent.leftNode == tcurrent) {
                tparent.leftNode = null;
            } else {
                tparent.rightNode = null;
            }
            if (this.root == current) {
                this.root = tcurrent;
            } else {
                if (parent.leftNode == current) {
                    parent.leftNode = tcurrent;
                } else {
                    parent.rightNode = tcurrent;
                }
            }
            current.leftNode = current.rightNode = null;
        } else {
            // 当前节点有一个子节点
            if (this.root == current) {
                this.root = current.leftNode == null ? current.rightNode : current.leftNode;
            } else {
                if (parent.leftNode == current) {
                    // 要删除的节点是父节点的左子树
                    parent.leftNode = current.leftNode == null ? current.rightNode : current.leftNode;
                } else {
                    // 要删除的节点是父节点的右子树
                    parent.rightNode = current.leftNode == null ? current.rightNode : current.leftNode;
                }
            }
        }
        return true;
    }
}

四、用数组表示二叉树

用数组表示二叉树是将数据保存到数组中，用数组的下标来代替二叉树中的引用。规则是：如果某个节点索引是index，那么它的左子树节点下标是：2*index+1，右子树节点是2*index+2，父节点是(index-1)/2。其中根节点的节点索引是0。这种数组结构对空间的利用率比较低，一般不常用。结构如图所示：

 五、完整的Java代码

这里的代码允许重复关键字的插入，但是删除或者是查询都只是对第一个匹配的Node节点进行操作。包括三部分代码，分别是Node.java，BinaryTree.java和Main.java。

public class Node<T> implements java.io.Serializable {

    private static final long serialVersionUID = -1180807550428965783L;
    /**
     * 节点数据对象
     */
    public final T data;
    /**
     * 指向左子树，如果为null，表示没有左子树
     */
    public Node<T> leftNode;
    /**
     * 指向右子树，如果为null，表示没有右子树
     */
    public Node<T> rightNode;

    public Node() {
        this(null);
    }

    public Node(T data) {
        this(data, null, null);
    }

    public Node(T data, Node<T> leftNode, Node<T> rightNode) {
        super();
        this.data = data;
        this.leftNode = leftNode;
        this.rightNode = rightNode;
    }

    @Override
    public String toString() {
        return "[data=" + data + ", leftNode=" + leftNode + ", rightNode=" + rightNode + "]";
    }
}

public class BinaryTree<T extends Comparable<T>> {
    private String orderSplit = " ";
    private Node<T> root;

    public BinaryTree() {
        super();
    }

    /**
     * 插入一个节点到树中
     * 
     * @param data
     */
    public void insertData(T data) {
        if (root == null) {
            root = new Node<T>(data);
        } else {
            Node<T> parent = null;
            Node<T> current = this.root;

            if (data == null) {
                while (current != null && current.data != null) {
                    parent = current;
                    current = current.leftNode;
                }
            } else {
                while (current != null) {
                    if (current.data == null) {
                        parent = current;
                        current = current.rightNode;
                    } else {

                        int t = data.compareTo(current.data);
                        if (t == 0) {
                            break;
                        } else if (t < 0) {
                            // data < current.data
                            parent = current;
                            current = current.leftNode;
                        } else {
                            parent = current;
                            current = current.rightNode;
                        }
                    }
                }
            }

            if (current == null) {
                Node<T> newNode = new Node<T>(data);
                if (parent.data == null || (data != null && data.compareTo(parent.data) >= 0)) {
                    parent.rightNode = newNode;
                } else {
                    parent.leftNode = newNode;
                }
            } else {
                current.rightNode = new Node<T>(data, null, current.rightNode);
            }
        }
    }

    /**
     * 在二叉搜索树中查询节点数据为data的节点，如果没有匹配的，那么返回null。
     * 
     * @param data
     * @return
     */
    public Node<T> find(T data) {
        Node<T> current = this.root;
        if (data == null) {
            while (current != null && current.data != null) {
                current = current.leftNode;
            }
        } else {
            while (current != null) {
                if (current.data == null) {
                    current = current.rightNode;
                } else {
                    int t = data.compareTo(current.data);
                    if (t == 0) {
                        break;
                    } else if (t < 0) {
                        // data < current.data
                        current = current.leftNode;
                    } else {
                        current = current.rightNode;
                    }
                }
            }
        }
        return current;
    }

    /**
     * 寻找最小值节点
     * 
     * @return
     */
    public Node<T> findMinDataNode() {
        Node<T> current = this.root;
        while (current != null && current.leftNode != null) {
            current = current.leftNode;
        }
        return current == null ? null : current;
    }

    /**
     * 寻找最大值节点
     * 
     * @return
     */
    public Node<T> findMaxDataNode() {
        Node<T> current = this.root;
        while (current != null && current.rightNode != null) {
            current = current.rightNode;
        }
        return current == null ? null : current;
    }

    /**
     * 删除data，如果有多个数据，值删除第一个
     * 
     * @param data
     * @return
     */
    public boolean delete(T data) {
        Node<T> parent = null;
        Node<T> current = this.root;

        if (data == null) {
            while (current != null && current.data != null) {
                parent = current;
                current = current.leftNode;
            }
        } else {
            while (current != null) {
                if (current.data == null) {
                    parent = current;
                    current = current.rightNode;
                } else {
                    int t = data.compareTo(current.data);
                    if (t == 0) {
                        break;
                    } else if (t < 0) {
                        // data < current.data
                        parent = current;
                        current = current.leftNode;
                    } else {
                        parent = current;
                        current = current.rightNode;
                    }
                }
            }
        }

        if (current == null) {
            return false;
        } else {
            // 当前节点不是根节点, parent不为null
            if (current.leftNode == null && current.rightNode == null) {
                // 当前节点没有子节点
                if (this.root == current) {
                    this.root = null;
                } else {
                    if (parent.leftNode == current) {
                        parent.leftNode = null;
                    } else {
                        parent.rightNode = null;
                    }
                }
            } else if (current.leftNode != null && current.rightNode != null) {
                // 当前节点有两个子节点
                Node<T> tparent = current;
                Node<T> tcurrent = current.rightNode;
                while (tcurrent.leftNode != null) {
                    tparent = tcurrent;
                    tcurrent = tcurrent.leftNode;
                }

                tcurrent.leftNode = current.leftNode;

                if (tparent.leftNode == tcurrent) {
                    tparent.leftNode = null;
                } else {
                    tparent.rightNode = null;
                }
                if (this.root == current) {
                    this.root = tcurrent;
                } else {
                    if (parent.leftNode == current) {
                        parent.leftNode = tcurrent;
                    } else {
                        parent.rightNode = tcurrent;
                    }
                }
                current.leftNode = current.rightNode = null;
            } else {
                // 当前节点有一个子节点
                if (this.root == current) {
                    this.root = current.leftNode == null ? current.rightNode : current.leftNode;
                } else {
                    if (parent.leftNode == current) {
                        // 要删除的节点是父节点的左子树
                        parent.leftNode = current.leftNode == null ? current.rightNode : current.leftNode;
                    } else {
                        // 要删除的节点是父节点的右子树
                        parent.rightNode = current.leftNode == null ? current.rightNode : current.leftNode;
                    }
                }
            }
            return true;
        }
    }

    /**
     * 前序遍历
     * 
     * @return
     */
    public String preorder() {
        return this.preorder(this.root);
    }

    private String preorder(Node<T> node) {
        StringBuffer sb = new StringBuffer();
        if (node != null) {
            sb.append(node.data).append(orderSplit);
            sb.append(this.preorder(node.leftNode));
            sb.append(this.preorder(node.rightNode));
        }
        return sb.toString();
    }

    /**
     * 中序遍历
     * 
     * @return
     */
    public String inorder() {
        return this.inorder(this.root);
    }

    private String inorder(Node<T> node) {
        StringBuffer sb = new StringBuffer();
        if (node != null) {
            sb.append(this.preorder(node.leftNode));
            sb.append(node.data).append(orderSplit);
            sb.append(this.preorder(node.rightNode));
        }
        return sb.toString();
    }

    /**
     * 后序遍历
     * 
     * @return
     */
    public String postorder() {
        return this.postorder(this.root);
    }

    private String postorder(Node<T> node) {
        StringBuffer sb = new StringBuffer();
        if (node != null) {
            sb.append(this.preorder(node.leftNode));
            sb.append(this.preorder(node.rightNode));
            sb.append(node.data).append(orderSplit);
        }
        return sb.toString();
    }

    @Override
    public String toString() {
        return "BinaryTree [root=" + root + "]";
    }
}

public class Main {
    public static void main(String[] args) {
        testBinaryTree2();
    }

    static void testBinaryTree2() {
        BinaryTree<String> tree = new BinaryTree<>();
        tree.insertData("D");
        tree.insertData("B");
        tree.insertData("F");
        tree.insertData("C");
//        tree.insertData("G");
//        tree.insertData("E");
        System.out.println(tree);
        System.out.println(tree.delete("D"));
        System.out.println(tree);
    }

    static void testBinaryTree1() {
        BinaryTree<String> tree = new BinaryTree<>();
        tree.insertData("D");
        tree.insertData("B");
        tree.insertData("F");
        tree.insertData("A");
        tree.insertData("G");
        tree.insertData("E");
        tree.insertData(null);
        tree.insertData(null);
        tree.insertData("C");
        tree.insertData("W");
        tree.insertData("O");
        tree.insertData("C");

        System.out.println(tree);

        System.out.println("**********************");
        System.out.println(tree.preorder());
        System.out.println(tree.inorder());
        System.out.println(tree.postorder());
        System.out.println(tree.findMaxDataNode());
        System.out.println(tree.findMinDataNode());
    }

}