大数据的矩阵计算基础（一）

矩阵

矩阵的概念：由m*n个a_ij（i=1,2,3,4...;j=1,2,3,4...)排成的有序列表。

可写成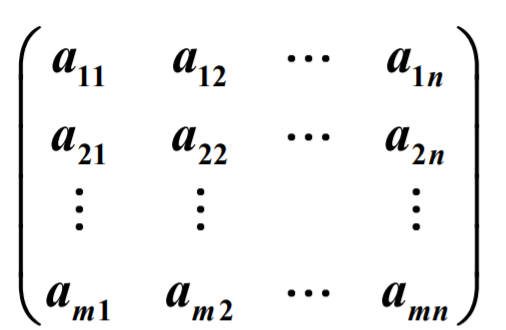：或。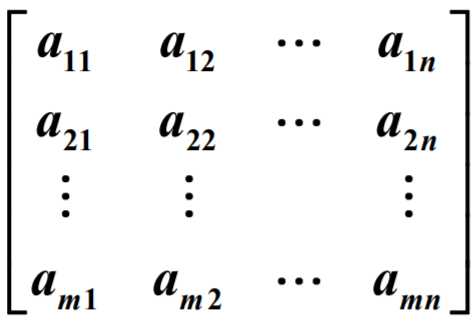

当m=n时，称矩阵A为n阶方阵。其中，从左上到右下的对角线称为主对角线，从右上到左下的对角线我们称为次对角线。

矩阵的类型介绍：

单位矩阵：主对角线上全为1，其他位置全是0的方阵称为单位矩阵，记为I或E。

负矩阵：对于矩阵A_mxn=(a_ij)_mxn，将矩阵A的各个元素都取相反数得到的矩阵称为矩阵A的负矩阵。

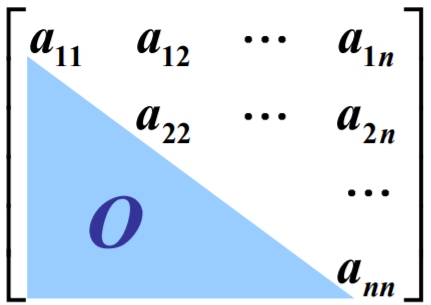上三角阵：         下三角阵：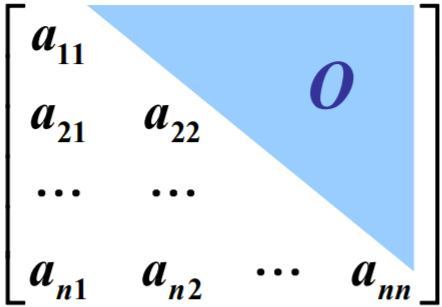

对角方阵：既是上三角阵，又是下三角阵（即只有对角线不为0，其余部分均为0的矩阵）称为对角方阵或对角矩阵。

数量矩阵：所有对角元a_ii均相等的矩阵称为数量矩阵。对角元的和∑a_ii称为方阵A的迹，记为trA。

零矩阵：所有元素全为0的矩阵称为零矩阵。不同阶数的零矩阵并不相等。

矩阵的运算：

加法：A_mxn+B_mxn=（a_ij+b_ij）

减法：A_mxn-B_mxn=（a_ij-b_ij）

数乘：k*A=（ka_ij）

交换律：A+B=B+A

结合律：（A+B）+C=A+（B+C）

零矩阵相关：A+0=A；A-A=0

1*A=A；0*A=0

结合率：（KI）A=K（IA）

分配率：（K+I）A=KA+IA；K（A+B）=KA+KB

乘法：若C_mxp=A_mxnxB_nxp，则有C_ij=a_i1b_1j+a_i2b_2j+a_i3b_3j+...+a_isb_sj。

如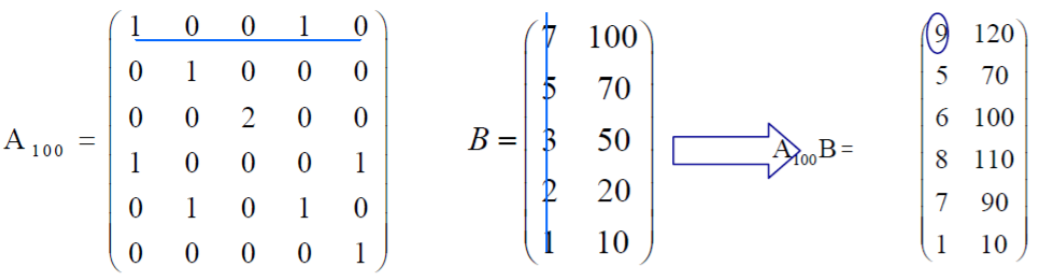：。1x7+0x5+0x3+1x2+0x1=9.

*两个矩阵相乘中：A的列数一定要与B的行数相等

由AB=0并不能推断出其中一个矩阵为零矩阵；由AB=AC也不能推断出B=C。

矩阵乘法运算律：

（AB）C=A（BC）

A（B+C）=AB+AC

（A+B）C=AC+AB

k（AB）=kAB=A（kB）

AI=IA=A

A0=0

若A是n阶方阵，则有：A^pA^q=A^pq；(A^p)^q=A^qp

当AB=BA时，有：(AB)^k=A^kB^k

矩阵的转置：A_mxn=（a_ij）_mxn，则A_mxn^T=B_mxn（a_ji）_mxn

转置的运算：（A^T）^T=A

（A+B）^T=A^T+B^T

（λA）^T=λA^T

（AB）^T=B^TA^T；（ABC）^T=C^TB^TA^T

对称矩阵：若A=A^T，则称A为对称矩阵

斜对称矩阵：若A=-A^T，则称A为斜对称矩阵

可逆矩阵：若对于方阵A，有方阵B使得AB=BA=I，则称A为可逆矩阵，矩阵B称为矩阵A的逆，记为B=A^-1

若A是可逆矩阵，则A的逆是唯一的。

若A、B可逆，则A^-1，AB，A^T，kA也是可逆的。

若A为可逆矩阵，等价于下面任一条件：

1、存在矩阵B使得AB=I

2、A的行向量组线性无关

3、存在矩阵B使得BA=I

4、A的列向量组线性无关

分块矩阵一般将矩阵分为四块，分块矩阵的乘法与矩阵的乘法运算相同。

分块矩阵的转置：若A=，则A^T=

二阶行列式：

二元一次方程组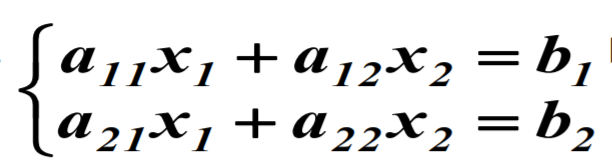的解为。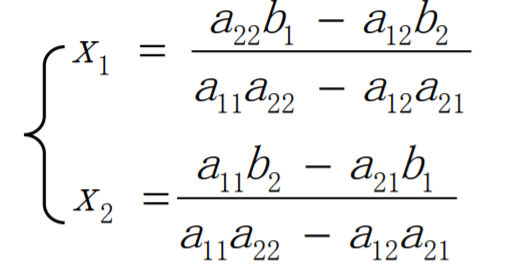

可将其简化记忆为：

其中：，，。

则有x₁=D₁/D，x₂=D₂/D

二阶行列式记为。其结果为主对角线减去次对角线的值。

三阶行列式也遵循对角线原则，如图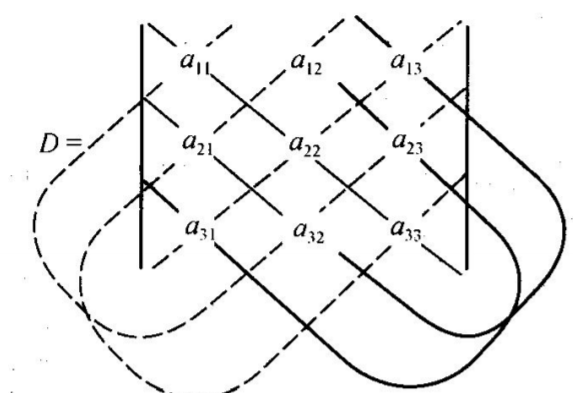：。即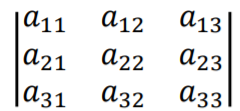=a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₁₃a₂₁a₃₂-a₃₁a₂₂a₁₃-a₂₁a₁₂a₃₃-a₂₃a₃₂a₁₁

对角矩阵的行列式等于对角线的乘积。

上三角矩阵行列式=下三角矩阵行列式=对角线乘积

行列式的性质：

1、单位矩阵的行列式等于1 ；

2、如果将行列式两行（或列）互换，则行列式的值改变符号；

3、行列式一行（或一列）的公因子可以提到行列式的外面；

4、若某行为0，或者两行相同或成比列，则行列式的值为0；

5、若行列式的某一行（或列）的元素都是两个数之和，则这个行列式是对应两个行列式的和；

6、detA=detA^T,detA表示A的行列式。

7、det（AB）=detAdetB

8、det（A^-1）=a/detA