算法

题目分析

给定n个整数组成的序列，要求将序列分割为m段，每段子序列中的数在原序列中连续排列，求使得子段和的最大值达到最小的分割方法

解题方法

状态转移方程

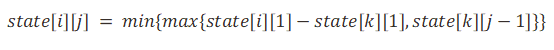
State[i][j]表示前i个数据分成j段得到的最大最小值，比较前k个数据的j-1分段的值与k到i的值的最大值，其中k到i的最大值为state[i][1]-state[k][1]

运行结果

 

代码

#include <iostream>
#include <algorithm>
using namespace std;
const int MAX_C = 100;
int state[MAX_C][MAX_C];
int a[MAX_C];
int Min(int n, int m) {
    int i, j, k, temp, Min;
    state[0][1] = 0;
    for (i = 1; i <= n; i++) {
        state[i][1] = state[i - 1][1] + a[i];
    }
    for (i= 2; i <= n; i++) {
        for (j =2; j <= m; j++) {
            temp = 1000000;
            for (k = 1; k < i; k++) {
                Min = state[i][1] - state[k][1] > state[k][j - 1] ? (state[i][1] - state[k][1]) : state[k][j - 1];
                if (temp > Min) temp = Min;
            }
            state[i][j] = temp;
        }
    }
    return state[n][m];
}
int main() {
    int n = 0, m = 0;
    int temp = 0;
    int Max = 0;
    while (cin >> n&&n) {
        cin >> m;
        memset(a, 0, sizeof(a));=
        for (int i = 1; i <= n; i++) {
            cin >> a[i];
        }
        memset(state, 0, sizeof(state));
        cout << Min(n, m) << endl;
    }
    return 0;
}