hdu 2196 Computer 树形dp

http://acm.hdu.edu.cn/showproblem.php?pid=2196

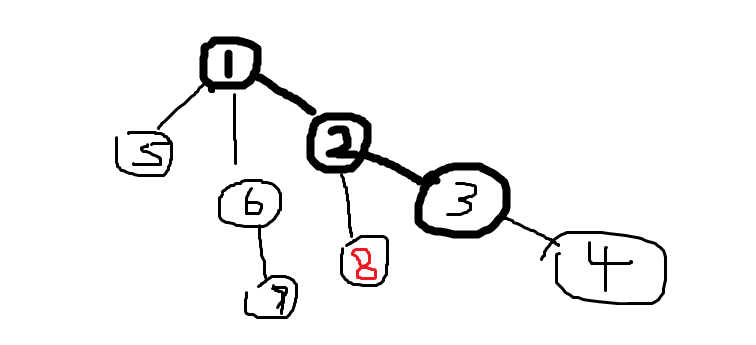
要统计第8号顶点的答案，那么可以来源于2部分。

1、8直接走下面的子树，这样就可能是最长距离。

2、8借助它的爸爸2，走了2能走的最长距离（这个不能经过8本身） +  e[2][8]

然后递归处理，2也是这样处理。2可以直接走它的子树，或者借助它的爸爸1来弄。

设dp[cur][0]表示第cur个节点，走它的子树，能走的最长的距离，dp[cur][1]表示第二长的距离，同样也是需要走cur的子树。

id[cur]表示第cur个节点中，走了最长的距离是经过哪一颗子树。这个用来后面的第二大距离判断 + 是否重复判断。

这样就可以算出ans[]了，

首先ans[1] = 0，为了不重复走路，

对于1的所有儿子v1....vk

ans[vk] = max(ans[1], dp[1][0 / 1]) + e[i].w，就是先求出借助爸爸能走的最长距离，然后再和自己的dp[cur][0]比较

因为我存的是有向图，只能靠爸爸来更新儿子，然后爸爸再更新真实值。

感觉这题挺难的`~~~刚入门树形dp。。就这样的题。。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <assert.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;


#include <iostream>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <bitset>
const int maxn = 10000 + 20;
struct node {
    int u, v, w, tonext;
}e[maxn * 2];
int first[maxn];
int num;
int n;
int dp[maxn][2], vis[maxn], id[maxn], DFN;
void add(int u, int v, int w) {
    ++num;
    e[num].u = u;
    e[num].v = v;
    e[num].w = w;
    e[num].tonext = first[u];
    first[u] = num;
}
int dfsone(int cur) {
    if (vis[cur] == DFN) return dp[cur][0];
    vis[cur] = DFN;
    int mx = 0, mxid = -inf;
    for (int i = first[cur]; i; i = e[i].tonext) {
        int v = e[i].v;
        int t = dfsone(v) + e[i].w;
        if (t > mx) {
            mx = t;
            mxid = i;
        }
    }
    dp[cur][0] = mx; //子树的是0
    id[cur] = mxid;
    //求second大
    int sec = 0;
    for (int i = first[cur]; i; i = e[i].tonext) {
        int v = e[i].v;
        if (i == id[cur]) continue;
        int t = dfsone(v) + e[i].w;
        if (t > sec) sec = t;
    }
    dp[cur][1] = sec;
    return dp[cur][0];
}
int ans[maxn]; //依靠爸爸能得到的最大值，然后最后dfstwo完后更新自己
int dfstwo(int cur) {
    for (int i = first[cur]; i; i = e[i].tonext) {
        int v = e[i].v;
        if (id[cur] == i) {
            ans[v] = max(ans[cur], dp[cur][1]) + e[i].w;
        } else {
            ans[v] = max(ans[cur], dp[cur][0]) + e[i].w;
        }
        dfstwo(v);
        ans[v] = max(ans[v], dp[v][0]); //更新真实值
    }
}
void work() {
    memset(first, 0, sizeof first);
    memset(ans, 0, sizeof ans);
    num = 0;
    ++DFN;
    for (int i = 2; i <= n; ++i) {
        int u, w;
        scanf("%d%d", &u, &w);
        add(u, i, w);
    }
    dfsone(1);
    ans[1] = 0;
    dfstwo(1);
    ans[1] = dp[1][0];
    for (int i = 1; i <= n; ++i) {
        printf("%d
", ans[i]);
    }
//    printf("
");
}
int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    while (scanf("%d", &n) != EOF) work();
    return 0;
}