Matrix Power Series POJ

矩阵幂次之和。

自己想着想着就想到了一个解法，但是还没提交，因为POJ崩了，做了一个FIB的前n项和，也是用了这个方法，AC了，相信是可以得。

提交了，是AC的

http://poj.org/problem?id=3233

我的思路是：

首先原矩阵保留着，然后需要扩大一倍

需要求1--->1的路径数 <= k的，ans = （路径数 = k的） ＋（路径数 < k）的

等于k的很容易求，就是e^k然后e[1][1]就是答案，那么小于k的，我们需要虚拟一个节点保留着

可以先看看这个http://www.cnblogs.com/liuweimingcprogram/p/6490034.html

然后新增一个节点3，e[1][3] = 1,  e[3][3] = 1是用来求 < k的数目的。

怎么求，比如

这样求到的e[1][1] = 1表明长度是2的有一种情况，但是长度是1的遗漏了，就是1--1本来那条，通过新增一条虚拟边e[1][3]

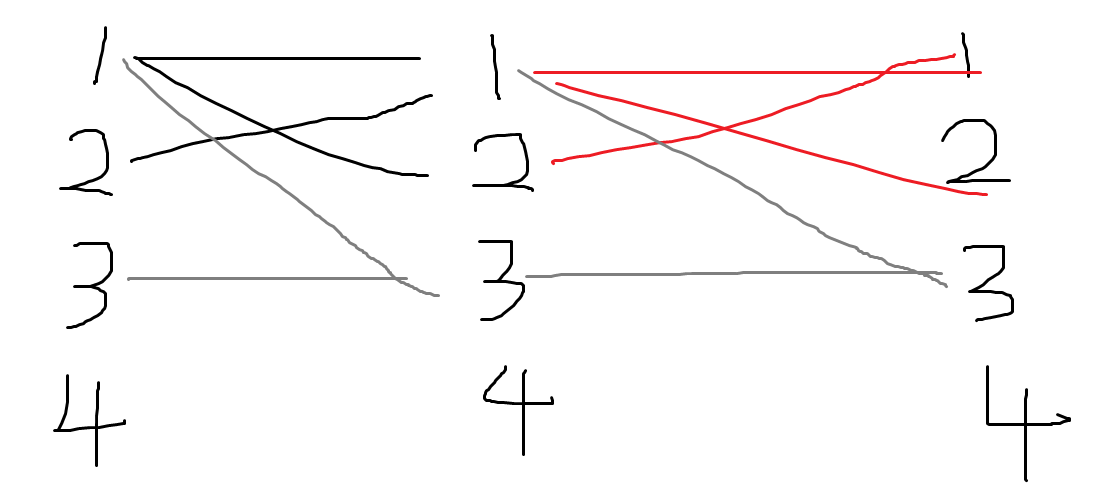
这样就把1--1原来的那条边保留了下来，

1-->3这条边是专为1服务的，是e[1][1]，也就是结尾点是1的情况的总数。所以会有一条e[3][3]的多余边，需要减去1。

而求1-->2的总数的时候，是e[1][2]（长度是k的总数） + e[1][4]（长度 < k的总数）这里就不会多出一条边了，因为本来的e[1][4] = 0的

这个是真真正正的保留了1--2这条边了。

具体自己画画吧，感觉描述不清楚了。

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 60 + 3;
struct Matrix {
    LL a[maxn][maxn];
    int row;
    int col;
}base;
//应对稀疏矩阵，更快。
struct Matrix matrix_mul(struct Matrix a, struct Matrix b, int MOD) { //求解矩阵a*b%MOD
    struct Matrix c = {0};  //这个要多次用到，栈分配问题，maxn不能开太大，
    //LL的时候更加是，空间是maxn*maxn的，这样时间用得很多，4和5相差300ms
    c.row = a.row; //行等于第一个矩阵的行
    c.col = b.col; //列等于第二个矩阵的列
    for (int i = 1; i <= a.row; ++i) {
        for (int k = 1; k <= a.col; ++k) {
            if (a.a[i][k]) { //应付稀疏矩阵，0就不用枚举下面了
                for (int j = 1; j <= b.col; ++j) {
                    c.a[i][j] += a.a[i][k] * b.a[k][j];
                    c.a[i][j] = (c.a[i][j] + MOD) % MOD; //负数取模
                }
            }
        }
    }
    return c;
}
struct Matrix quick_matrix_pow(struct Matrix ans, struct Matrix base, int n, int MOD) {
//求解a*b^n%MOD
    while (n) {
        if (n & 1) {
            ans = matrix_mul(ans, base, MOD);//传数组不能乱传,不满足交换律
        }
        n >>= 1;
        base = matrix_mul(base, base, MOD);
    }
    return ans;
}
int n, k, MOD;
void work() {
    base.row = base.col = 2 * n;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            cin >> base.a[i][j];
            base.a[i][j] %= MOD;
        }
    }
    for (int i = 1; i <= n; ++i) {
        base.a[i][n + i] = 1;
    }
    for (int i = n + 1; i <= 2 * n; ++i) {
        base.a[i][i] = 1;
    }
//    for (int i = 1; i <= 2 * n; ++i) {
//        for (int j = 1; j <= 2 * n; ++j) {
//            printf("%d ", base.a[i][j]);
//        }
//        printf("
");
//    }
    Matrix I = {0};
    I.row = I.col = 2 * n;
    for (int i = 1; i <= 2 * n; ++i) {
        I.a[i][i] = 1;
    }
//    printf("
");
    I = quick_matrix_pow(I, base, k, MOD);
//    for (int i = 1; i <= 2 * n; ++i) {
//        for (int j = 1; j <= 2 * n; ++j) {
//            printf("%d ", I.a[i][j]);
//        }
//        printf("
");
//    }
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= n; ++j) {
            int ans = 0;
            ans += I.a[i][j];
            ans += I.a[i][n + j];
            ans %= MOD;
            if (i == j) ans = (ans - 1 + MOD) % MOD;
            printf("%d ", ans);
        }
        printf("
");
    }
}

int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    while (cin >> n >> k >> MOD) work();
    return 0;
}

做了这个题

http://acm.hdu.edu.cn/showproblem.php?pid=5171

#include <bits/stdc++.h>
#define IOS ios::sync_with_stdio(false)
using namespace std;
#define inf (0x3f3f3f3f)
typedef long long int LL;
const int maxn = 6;
struct Matrix {
    LL a[maxn][maxn];
    int row;
    int col;
}base;
//应对稀疏矩阵，更快。
struct Matrix matrix_mul(struct Matrix a, struct Matrix b, int MOD) { //求解矩阵a*b%MOD
    struct Matrix c = {0};  //这个要多次用到，栈分配问题，maxn不能开太大，
    //LL的时候更加是，空间是maxn*maxn的，这样时间用得很多，4和5相差300ms
    c.row = a.row; //行等于第一个矩阵的行
    c.col = b.col; //列等于第二个矩阵的列
    for (int i = 1; i <= a.row; ++i) {
        for (int k = 1; k <= a.col; ++k) {
            if (a.a[i][k]) { //应付稀疏矩阵，0就不用枚举下面了
                for (int j = 1; j <= b.col; ++j) {
                    c.a[i][j] += a.a[i][k] * b.a[k][j];
                    c.a[i][j] = (c.a[i][j] + MOD) % MOD; //负数取模
                }
            }
        }
    }
    return c;
}
struct Matrix quick_matrix_pow(struct Matrix ans, struct Matrix base, int n, int MOD) {
//求解a*b^n%MOD
    while (n) {
        if (n & 1) {
            ans = matrix_mul(ans, base, MOD);//传数组不能乱传,不满足交换律
        }
        n >>= 1;
        base = matrix_mul(base, base, MOD);
    }
    return ans;
}
const int MOD = 10000007;
int n, k;
int a[100000 + 20];
void work() {
    for (int i = 1; i <= n; ++i) cin >> a[i];
    sort(a + 1, a + 1 + n);
    Matrix I = {0};
    I.row = I.col = 4;
    for (int i = 1; i <= 4; ++i) I.a[i][i] = 1;
    I = quick_matrix_pow(I, base, k, MOD);
    Matrix F = {0};
    F.row = 1, F.col = 2;
    F.a[1][1] = a[n], F.a[1][2] = a[n - 1];
    Matrix b = {0};
    b.row = b.col = 2;
    for (int i = 1; i <= 2; ++i) {
        for (int j = 1; j <= 2; ++j) {
            int ans = I.a[i][j];
            ans += I.a[i][2 + j];
            ans %= MOD;
            if (i == j) ans = (ans - 1 + MOD) % MOD;
            b.a[i][j] = ans;
        }
    }
//    for (int i = 1; i <= 2; ++i) {
//        for (int j = 1; j <= 2; ++j) {
//            printf("%d ", b.a[i][j]);
//        }
//        printf("
");
//    }
    F = matrix_mul(F, b, MOD);
    int ans = F.a[1][1];
    for (int i = 1; i <= n; ++i) {
        ans = (ans + a[i]) % MOD;
    }
    cout << ans << endl;
}

int main() {
#ifdef local
    freopen("data.txt", "r", stdin);
//    freopen("data.txt", "w", stdout);
#endif
    base.col = base.row = 4;
    base.a[1][1] = 1, base.a[1][2] = 1;
    base.a[2][1] = 1, base.a[2][2] = 0;
    for (int i = 1; i <= 2; ++i) {
        base.a[i][2 + i] = 1;
    }
    for (int i = 3; i <= 4; ++i) base.a[i][i] = 1;
    while (cin >> n >> k) work();
    return 0;
}