图论是NOIP必考的知识点。
松弛操作
如图: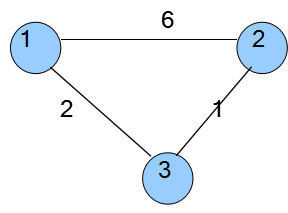
比如说从1到2可以有2种解法,一种是直接走,另一种就是用一个点来中转;
从这两条路上选最短的走法的操作就叫松弛。
根据这个操作啊就可以做出像暴力一样的最短路算法————Floyd算法.
我们可以先初始化把不相连的边都设为无穷大,再不断进行松弛操作不断更新最短路。
这样就可以得出所有的两点之间的最短路,还能处理负边权。
不过就是有点慢时间复杂度是O(n3)
for(k=1;k<=n;k++) //中转点
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(dis[i][j]>dis[i][k]+dis[k][j]) //松弛操作
dis[i][j]=dis[i][k]+dis[k][j];
但是该算法适用于求解多源最短路径,所以时间复杂度大也是正常的。
而单源最短路径主要有两种
Dijkstra算法O(n2)加堆优化O(nlogn)
用来计算从一个点到其他所有点的最短路径的算法。
Dijkstra它不能处理存在负边权的情况。
算法描述:
设起点为s,dis[v]表示从s到v的最短路径,。
a)初始化:dis[v]=∞(v≠s); dis[s]=0;;
b)For (i = 1; i <= n ; i++)
1.在没有被访问过的点中找一个顶点u使得dis[u]是最小的。(可以认为是贪心操作)
2.u标记为已确定最短路径的点
3.与u相连的每个没有被确定最短路径的顶点进行松弛操作。
算法思想:我们把点分为两类,一类是已确定最短路径的点,称为“白点”,另一类是未确定最短路径的点,称为“蓝点”。如果我们要求出一个点的最短路径,就是把这个点由蓝点变为白点。从起点到蓝点的最短路径上的中转点在这个时刻只能是白点。
Dijkstra的算法思想,就是一开始将起点到起点的距离标记为0,而后进行n次循环,每次找出一个到起点距离dis[u]最短的点u,将它从蓝点变为白点。随后枚举所有的蓝点vi,如果以此白点为中转到达蓝点vi的路径dis[u]+w[u][vi]更短的话,这将它作为vi的“更短路径”dis[vi](此时还不确定是不是vi的最短路径)。
就这样,我们每找到一个白点,就尝试着用它修改其他所有的蓝点。中转点先于终点变成白点,故每一个终点一定能够被它的最后一个中转点所修改,而求得最短路径。
例题:
luogu p[3371]
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; bool b[500010]; long long dis[500010],lin[500010],tot,n,m,s; struct cym{ int from,to,len,next; }e[2000010]; int main() { scanf("%d%d%d",&n,&m,&s); for(int i=1;i<=n;i++) dis[i]=2147483647; for(int i=1;i<=m;i++) { int a,b,c; scanf("%d%d%d",&a,&b,&c); e[++tot].from=a; e[tot].to=b; e[tot].len=c; e[tot].next=lin[a]; lin[a]=tot; } dis[s]=0; for(int i=1;i<=n;i++) { int minn=2147483647; int k=0; for(int j=1;j<=n;j++) if(minn>dis[j]&&!b[j]) { minn=dis[j]; k=j; } b[k]=1; for(int j=lin[k];j;j=e[j].next) if(dis[e[j].to]>dis[k]+e[j].len) dis[e[j].to]=dis[k]+e[j].len; } for(int i=1;i<=n;i++) { printf("%lld ",dis[i]); } }
除了这种算法,还有两个思想相同但速度不一样的算法。
一个是SPFA,一个是Bellman_ford算法。
这两种算法的思想都一样,但是SPFA是有队列优化的,所以介绍SPFA算法。
也是一个单源最短路径算法,但是不同的是他的速度一般是要比dijkstra要快的,且它可以处理负边权,甚至还可以判负环,但是容易被卡,所以如果在比赛中时间真的充足的话,还是建议写堆优化dijkstra。
算法描述:
设起点为s,dis[v]表示从s到v的最短路径,vis[i]数组表示i是否在队中。
a)初始化:dis[v]=∞(v≠s); dis[s]=0;
将s入队,vis[i]=1.
b)while(!q.empty())
1.取出队首u,并将vis数组设为零。
2.与u相连的每个没有被确定最短路径的顶点进行松弛操作。
3.如果被确定最短路径的顶点没有在队中,入队。
算法思想:动态逼近法
设立一个先进先出的队列用来保存待优化的结点,优化时每次取出队首结点u,并且用u点当前的最短路径估计值对离开u点所指向的结点v进行松弛操作,
如果v点的最短路径估计值有所调整,且v点不在当前的队列中,就将v点放入队尾。这样不断从队列中取出结点来进行松弛操作,直至队列空为止。
代码(题目同上):
#include<iostream> #include<cstdlib> #include<cstdio> #include<algorithm> #include<queue> #include<cstring> using namespace std; queue<long long>q; long long v[1000010],minn[1000100]; long long n,m,s,lin[1000010],tot=0; struct min_road{ long long from,to,next,len; }e[1000010]; void add(long long f,long long t,long long l) { e[++tot].from=f; e[tot].to=t; e[tot].len=l; e[tot].next=lin[f]; lin[f]=tot; } int main() { scanf("%lld%lld%lld",&n,&m,&s); for(int i=1;i<=n;i++)minn[i]=2147483647; for(int i=1;i<=m;i++) { long long f,t,l; scanf("%lld%lld%lld",&f,&t,&l); add(f,t,l); } q.push(s); v[s]=1; minn[s]=0; while(!q.empty()) { long long cur=q.front(); q.pop(); v[cur]=0; for(long long i=lin[cur];i;i=e[i].next) { if(minn[e[i].to]>minn[cur]+e[i].len) { minn[e[i].to]=minn[cur]+e[i].len; if(!v[e[i].to]) { q.push(e[i].to); v[e[i].to]=1; } } } } for(int i=1;i<=n;i++) printf("%lld ",minn[i]); }
讲完了图论的最短路算法,还有最小生成树算法。
如果一个图有n个点,那么如果有n-1条边。那么他一定是一棵树。
反之也成立。
克鲁斯卡尔算法即是一种解决最小生成树的算法。
算法思想:
我们用一种并查集的数据结构,用来判断该边是否在生成树中。
如果要想生成树最小,即可以贪心将每一条边的权值都排一下序。
然后逐个判断是否在树中,如果没有就加上,且合并,用并查集维护连通性。
反之就继续,直到全都判断完毕或已经出现一棵树。
代码(洛谷p3366)
#include<bits/stdc++.h> using namespace std; int fa[200001]; struct edge{ int u; int v; int w; }e[200001]; int cmp(edge a,edge b) { return a.w<b.w; } int find(int x) { return fa[x]==x?x:fa[x]=find(fa[x]); } long long cnt=0; long long ans=0; long long n,m; int main() { cin>>n>>m; for(int i=1;i<=n;i++) fa[i]=i; for(int i=1;i<=m;i++) cin>>e[i].u>>e[i].v>>e[i].w; sort(e+1,e+1+m,cmp); for(int i=1;i<=m;i++) { if(cnt==n-1) break; int x=find(e[i].u); int y=find(e[i].v); if(x!=y) { ans+=e[i].w; fa[y]=x; cnt++; } } if(cnt!=n-1) { cout<<"orz"; return 0; } cout<<ans; return 0; }