参考:https://www.cnblogs.com/fengfenggirl/p/lsh.html
https://blog.csdn.net/qq_29883591/article/details/63252946
一、引入
LSH就是对高维空间的数据进行近邻搜索的一种算法。它的原则是:原来在高维空间中就很接近的点,如果能够设计一种hash函数,使得它们的哈希值很大概率是一样的,那么再给一个新的高维空间上的点,再用这个hash函数得到一个哈希值,则哈希值相同的点是有很大概率在原来的高维空间上是近似的。总之,LSH就是降维+查找匹配的算法。
二、Jaccard相似度
Jaccard相似度就是交集除以并集。用于比较有限样本集之间的相似性与差异性。Jaccard系数值越大,样本相似度越高。

比如说我们要比较人们的购物袋中,啤酒和奶粉的相似度,也就是说我们想要找到有多少人的购物袋里会同时出现啤酒和奶粉。那我们就去数一下同时存在啤酒奶粉的购物袋有几个,再数一下所有的购物袋,二者相除即可得到结果。、
Jaccard重点关注的是交集部分。
三、shingling
一篇文档可以看成是一个字符串,文档的k-shingle为在该文档中长度为k的所有子串。任意一篇文档都可以表示为k-shingles的集合,比如“A document is a string of characters”这句话的所有3-shingles为{ ”A d”, ”do”, ”doc”, ”ocu”, ”cum”, ”ume”, ”men”, ”ent”, . . . , ”ers” }。
如果k非常小,那么k个字符的序列会出现在大多数的文档中,如k=1,许多文档都有相同的字符,几乎所有的文档都有很高的相似性。如果k应该足够大,那么对于给定的shingle出现在不同的文档中的概率是非常低的。比如这两个单词“ document”和“monument”:
SIM( { d, o, c, u, m, e, n, t } , { m, o,n, u, m, e, n, t } ) = 6/8
SIM( { doc, ocu, cum, ume, men, ent } ,{mon, onu, num, ume, men, ent } ) = 3/9
可以看见,k为3时比k为1时的Jaccard相似度要低很多。
四、矩阵表示
我们用列来表示文档集合,行来表示shingle,也就是上面提到的字符子串:
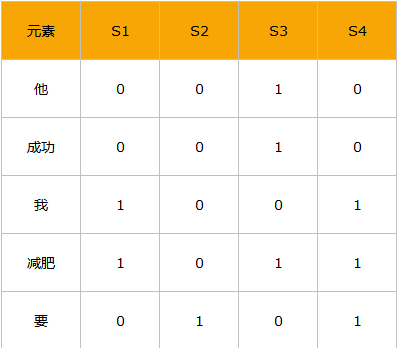
注意这里的行列都不是按顺序的,是经过打乱的。如果r行是c列的集合元素,就将矩阵的r行c列设置为1,否则为0。
最小哈希值:h(S1)=3,h(S2)=5,h(S3)=1,h(S4)=3.最小哈希值就是该列首次出现1的行数
为什么定义最小hash?事实上,两个集合经过随机排列转换之后得到的两个最小哈希值相等的概率等于这两个集合的Jaccard相似度,换句话说,两列最小hash值同等的概率与其相似度相等,即P(h(Si)=h(Sj)) = sim(Si,Sj)。为什么会相等?我们考虑Si和Sj这两列,它们所在的行的所有可能结果可以分成如下三类:
(1)A类:两列的值都为1;
(2)B类:其中一列的值为0,另一列的值为1;
(3)C类:两列的值都为0.
特征矩阵相当稀疏,导致大部分的行都属于C类,但只有A、B类行的决定sim(Si,Sj),假定A类行有a个,B类行有b个,那么sim(si,sj)=a/(a+b)。现在我们只需要证明对矩阵行进行随机排列,两个的最小hash值相等的概率P(h(Si)=h(Sj))=a/(a+b),如果我们把C类行都删掉,那么第一行不是A类行就是B类行,如果第一行是A类行那么h(Si)=h(Sj),因此P(h(Si)=h(Sj))=P(删掉C类行后,第一行为A类)=A类行的数目/所有行的数目=a/(a+b),这就是最小hash的神奇之处。
but这只是一次随机事件而已,我们可以看到S1文档和S4文档的哈希值相同,但是如果我们把上述表格中的行顺序【他,成功,我,减肥,要】换成【要,他,成功,我,减肥】,也就是把最后一行放在第一行而已,这时候再看S1和S4的最小哈希值h(S1)=4,h(S4)=1,哈希值就不一样了。那只是换了一个行的排列位置就会改变两个集合的Jaccard相似度?再看一遍上面标红的话:两个集合经过随机排列转换之后得到的两个最小哈希值相等的概率等于这两个集合的Jaccard相似度。注意,这里只是两个最小哈希值的概率!!!说明仅仅通过恰好一次的最小哈希值相同不能得出两个集合相似的结论!!!大数定理告诉我们,要重复多次,我们要把行进行多次排列组合!计算每次的哈希值,才能估计两个集合之间的相似度!这里有5个元素,那么我们的行排列组合就要有5*4*3*2*1种可能,然后每种可能下的四个文档的哈希值是不同的,也就是说不同可能下的哈希函数结果是不一样的,那么这里经过排列组合一共会得出5*4*3*2*1*4种哈希结果,接下来就要考虑怎么利用这些值进行相似度估计了。
五、最小哈希签名
我们假设shingles有n个排列组合的可能,每个可能下的哈希函数用hi来表示,就有n个哈希函数,也就是说有n组文档的哈希值,每个文档在n种shingles排列组合下有n个哈希值,那我们就可以针对每个文档Si,构建最小哈希签名向量了[h1(Si),h2(Si),.......,hn(Si)],按道理来说,像上面的例子只有4个文档,只要把4个文档的最小哈希签名向量合并起来就可以了,但是,这个n可能是很大的,虽然我们不必要取遍历排列组合的所有可能,但是对于大规模的矩阵进行显示排列转换是不可行的,非常消耗时间。
我们可以引入一个随机哈希函数来模拟随机排列转换的效果
例如:在此考虑图1对应的特征矩阵,我们在后面加上一些数据形成图3。另外将每一行替换成其对应的行号0,1,.....,4。选择的两个哈希函数分别为h1(x)=x+1 mod 5及h2(x)=3x+1 mod 5.两个哈希函数产生的结果显示在图3-4中的最后两列。注意到这里的两个简单哈希函数对应真正的行排列转换,当然这里这有当行数目为质数(这里为5, 这是为了避免不同的数之间具有相同的约数而导致余数会相等进而会被分配到一个桶号中,这就会产生冲突了)时才会有真正的排列转换。通常来说,哈希结果都会存在冲突,即至少有两行得到的哈希值相等。
接下来 模拟计算签名矩阵的算法。一开始,签名矩阵全部都由∞构成:
首先 ,考虑图3中的第0行。此时,不论是h1(0)还是h2(0)的结果都是1。而只有集合S1和S4在第0行为1,因此签名矩阵中只有这两列的值需要修改。因为1<∞,因此实际上是对S1和S4的对应值进行修改,所以当前签名矩阵的估计结果为: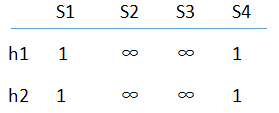
接下来,我们下移到图3中的第一行。对于该行,只有S3的值为1,此时其哈希值为h1(1)=2,h2(1)=4。因此,SIG(1,3)置为2,SIG(2,3)置为4。因为第一行中其它列的值均为0,所以签名矩阵的相应列的元素保持不变。于是,新的签名矩阵为:
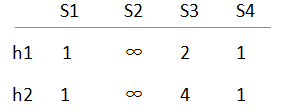
图3第2行中只有S2和S4对应的列的值为1,且其哈希值h1(2)=3,h2(2)=2,。S4对应的标签名本应修改,但是签名矩阵中对应列值为[1,1],因此其签名最后不会修改。而S2对应的列中仍然是初始值∞,我们将其修改为[3,2],得到如下图:
再接下来处理图3中的第3行。此时只有S2对应的列的值不为1。而哈希值h1(3)=4,h2(3)=0。h1的结果已经超过了矩阵中所有列上的已有值,因此不需要修改签名矩阵的第一列的任一值。然而,h2的值为0小于矩阵元素,因此将SIG(2,1)、SIG(2,3)及SIG(2,4)减小为0。需要注意的是,由于图3中S2列在当前行的取值已经为0,因此SIG(2,2)不可能再减小。于是,此时得到的签名矩阵为:
最后考虑图3中的第4行,此时h1(4)=0,h2(4)=3。由于第4行只在S3列取值为1,我们仅仅比较S3的当前值[2,0]与哈希值[0,3]即可。由于0<2,因此将SIG(1,3)改为0,而同时由于 3>0,因此SIG(2,3)保持不变。最终得到的签名矩阵为:
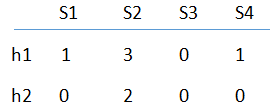
基于上述签名矩阵,可以估计原始集合之间的Jaccard相似度。注意到在签名矩阵中S1和S4对应的列向量完全相同,因此我们可以猜测SIM(S1,S4)=1.0。如果回到图3,会发现S1和S4的真是Jaccard相似度为2/3.需要记住的是,签名矩阵中行之间的一致程度只是真实Jaccard相似度的一个估计值,因为本例规模太小,所以并不足以说明在大规模数据情况下估计值和真实值相近的规律。另外,在本例中,S1和S3在签名矩阵中有一半元素一致(真实相似度为1/4),而S1和S2在签名矩阵中没有相同元素,所以相似度估计值为0(真实相似度也为0)。
六、基于最小哈希签名的局部敏感哈希
针对上面得到的签名矩阵,对行进行分组,分组之后,我们对最小签名向量的每一组进行hash,各个组设置不同的桶空间。只要两列有一组的最小签名部分相同,那么这两列就会hash到同一个桶而成为候选相似项。签名的分析我们知道,对于某个具体的行,两个签名相同的概率p =两列的相似度= sim(S1,S2)。
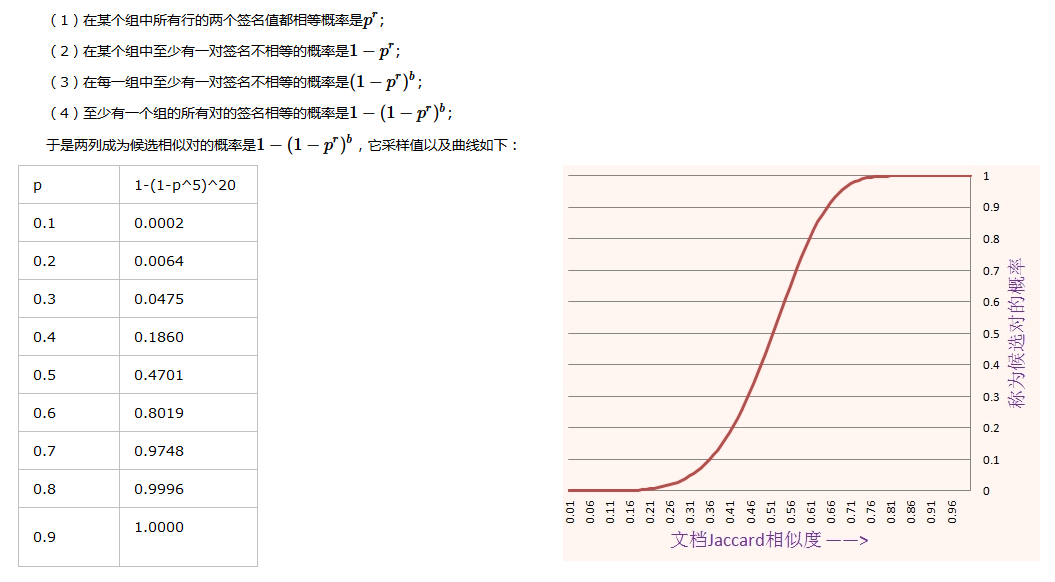
当两篇文档的相似度为0.8时,它们hash到同一个桶而成为候选对的概率是0.9996,而当它们的相似度只有0.3时,它们成为候选对的概率只有0.0475,因此局部敏感hash解决了让相似的对以较高的概率hash到同一个桶,而不相似的项hash到不同的桶的问题。