剑指offer：二分查找找到旋转数组中的最小值

一、旋转数组

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转，例如[45123]就是[12345]的一个旋转。

二、题目分析

输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。

先考虑递增数组的旋转，如[12345]的一个旋转[45123]，可以知道旋转过后可以分成两组数字，两组数字分别递增，且最小值位于两组数字的中间，二分查找算法不限于运用在有序数组上。如果能够明确二分之后，答案存在于二分的某一侧，就可以使用二分：

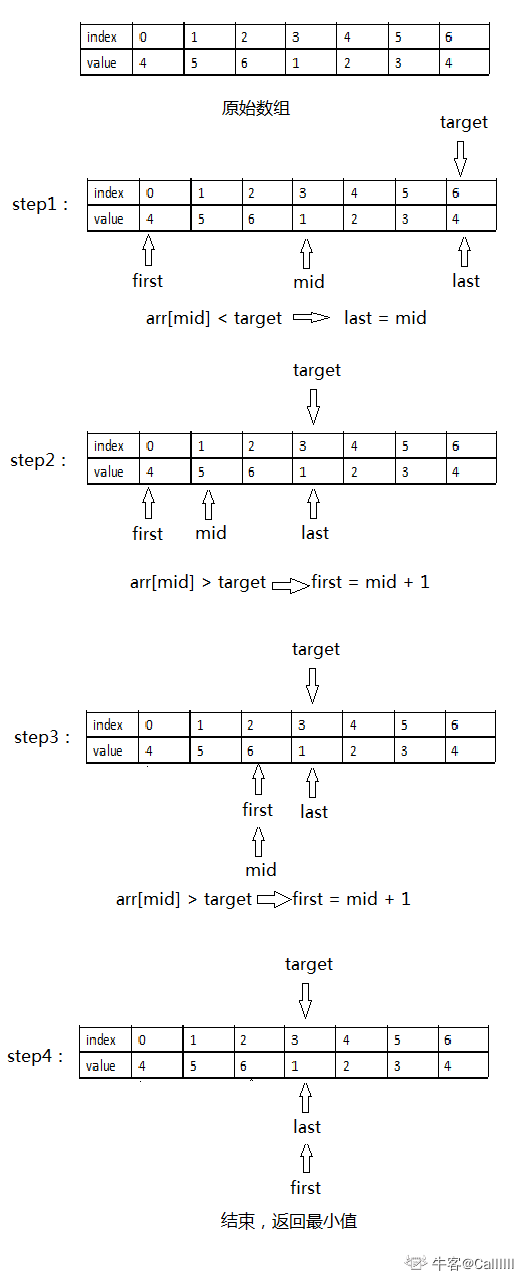
这里我们把target 看作是右端点，来进行分析，那就要分析以下三种情况，看是否可以达到上述的目标。

1. 情况1，arr[mid] > target：4 5 6 1 2 3
   • arr[mid] 为 6， target为右端点 3， arr[mid] > target, 说明[first ... mid] 都是 >= target 的，因为原始数组是非递减，所以可以确定答案为 [mid+1...last]区间,所以 first = mid + 1
2. 情况2，arr[mid] < target:5 6 1 2 3 4
   • arr[mid] 为 1， target为右端点 4， arr[mid] < target, 说明答案肯定不在[mid+1...last]，但是arr[mid] 有可能是答案,所以答案在[first, mid]区间，所以last = mid;
3. 情况3，arr[mid] == target:
   • 如果是 1 0 1 1 1， arr[mid] = target = 1, 显然答案在左边
   • 如果是 1 1 1 0 1, arr[mid] = target = 1, 显然答案在右边
     所以这种情况，不能确定答案在左边还是右边，那么就让last = last - 1;慢慢缩少区间，同时也不会错过答案。

总之，对于情况1的大于情况来说，需要将数组左端切除，即调整first=mid+1；对于情况2的小于情况来说，需要切除数组右端，且mid有可能是答案，所以调整last=mid

 三、python代码实现

class Solution:
    def minNumberInRotateArray(self, rotateArray):
        # write code here
        if rotateArray==[]:
            return 0
        elif len(rotateArray)==1:
            return rotateArray[0]
        elif len(rotateArray)==2:
            if rotateArray[0]<=rotateArray[1]:
                return rotateArray[0]
            else:
                return rotateArray[1]
        else:
            start=0
            end=len(rotateArray)-1
            mid=0
            while end>start:
                mid=(start+end)//2
                if rotateArray[start]<rotateArray[end]:
                    return rotateArray[start]
                elif rotateArray[mid]>rotateArray[start]:
                    start=mid+1
                elif rotateArray[mid]<rotateArray[end]:
                    end=mid
                else:
                    start+=1
            return rotateArray[end]