主题模型在机器学习和自然语言处理等领域是用来在一系列文档中发现抽象主题的一种统计模型。直观来讲,如果一篇文章有一个中心思想,那么一些特定词语会更频繁的出现。比方说,如果一篇文章是在讲狗的,那「狗」和「骨头」等词出现的频率会高些。如果一篇文章是在讲猫的,那「猫」和「鱼」等词出现的频率会高些。而有些词例如「这个」、「和」大概在两篇文章中出现的频率会大致相等。但真实的情况是,一篇文章通常包含多种主题,而且每个主题所占比例各不相同。因此,如果一篇文章 10% 和猫有关,90% 和狗有关,那么和狗相关的关键字出现的次数大概会是和猫相关的关键字出现次数的 9 倍。一个主题模型试图用数学框架来体现文档的这种特点。主题模型自动分析每个文档,统计文档内的词语,根据统计的信息来断定当前文档含有哪些主题,以及每个主题所占的比例各为多少。主题模型最初是运用于自然语言处理相关方向,但目前已经延伸至生物信息学等其它领域。
一、主题模型历史

二、直观理解主题模型
听名字应该就知道他讲的是什么?假如有一篇文章text,通过里面的词,来确定他是什么类型的文章,如果文章中出现很多体育类的词,比如,篮球,足球之类的,那么主题模型就会把它划分为体育类的文章。
因为主题模型涉及比较多的数学推导,所以我们先用一个小栗子,理解它要做的事。假设有这么一个场景:
- 一个资深HR收到一份应聘算法工程师的简历,他想仅仅通过简历来看一下这个人是大牛,还是彩笔,他是怎么判断呢?
他的一般做法就是拿到这份简历,看这个人的简历上写的内容包括了什么?
在此之前呢,他也一定是接触了很多算法工程师的面试,他根据这些招进来的人判断,一个大牛,有可能是:
- 穿条纹衬衫
- 曾在BAT就职
- 做过大型项目
这个HR就会看这个面试者是不是穿条纹衬衫,有没有在BAT就职过,做过什么牛逼的项目,如果都满足条件,那这个HR就会判断这个人应该是大牛,如果他只是穿条纹衬衫,没做过什么拿得出手的项目,那就要犹豫一下了,因为他是彩笔的可能性比较大。
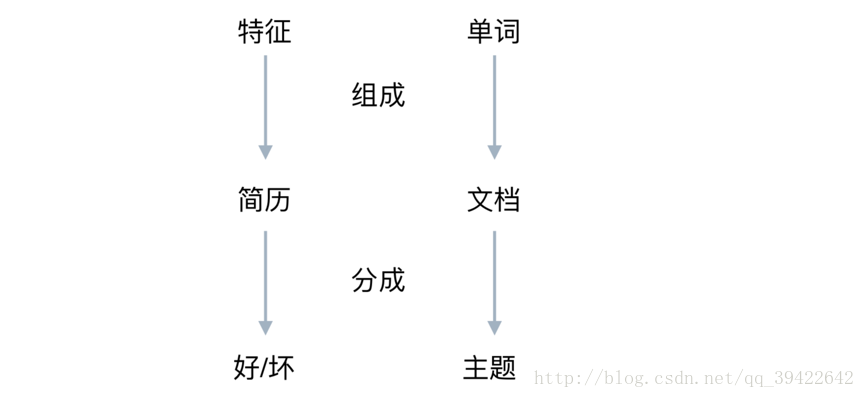
这个例子和主题模型的关系可以用这个图表示:
三、几种主题模型简介
3.1 TF-IDF
早在上世纪 80 年代,研究者们常常使用 TF-IDF 法来进行文档的检索和信息的提取。
在 TF-IDF 方法中,先选择一个基于词或者词组的基本词汇,然后对于语料库中的每个文档,分别统计其中每个单词的出现次数。经过合适的正则化后,再将词的频率计数和反向文档频率计数相比较,得到一个词数乘以文档数的向量 X。向量的每个行中都包含着语料库中每个文档的 TF-IDF 值。
IF 和 IDF 的概念见下:
$$tf_{i,j}=frac {n_{i,j}}{sum_k n_{k,j}}$$
其中$tf_{i,j}$是该词在文件$d_j$中出现的次数,分母表示文件$d_j$中所有字词的出现次数之和。
$$idf_i =log frac {|D|}{|{j:t_i in d_j}|}$$
|D|是语料库中的文件总数,$|{j:t_i in d_j}|$ 表示包含词语 $t_i$ 的文件数目。如果词语不在语料库中,为了避免分母为零的情况,一般会加上1.
$$tfidf_{i,j} = tf_{i,j} imes idf_{i,j}$$
对于某一特定文件中的高频词语,如果含有该词语的文档在整个文件集中是低频的,则我们可以得到一个较大的TF-IDF的值。因此,TF-IDF倾向于过滤去常见的词语,保留重要的词语。
但是整个TF-IDF算法是建立在一个假设之上的:一个单词出现的文本频数越小,它区别不同类别文本的能力就越大。这个假设很多时候是不正确的,尤其是在引入IDF的过程中,单纯地认为文本频率小的单词就越重要,文本频率大的单词就越无用,显然这并不是完全正确的。其也不能有效地反映单词的重要程度和特征词的分布情况,因此精度有限。
3.2 LSA 隐形语言分析
如果说TF-IDF算法体现的是文档中词出现的频率的情况,那么LSA则更进了一步,其目的是为了从文本中发现隐含的topic。
在文档的空间向量模型中,文档被表示成由特征词出现概率组成的多维向量,这种方法可以通过对不同词赋予不同的权重,应用于文本检索、分类以及聚类等问题中。然而这种空间向量模型没有能力处理一词多义以及一义多词这类问题。同义词也分别被表示成独立的一维,计算向量的余弦相似度时会低估用户期望的相似度,而某个词项有多个词义时,始终对应同一维度,因此计算的结果会高估用户期望的相似度。
而LSA的方法就减轻了类似的问题。LSA使用矩阵的奇异值分解来确定一个在 TF-IDF 特征空间中的线性子空间,实现大幅压缩以及对同义和一词多义等基本语言概念的捕捉。
通过SVD分解,我们可以构造一个原始向量矩阵的一个低秩逼近矩阵,具体的做法是将词项文档矩阵做SVD分解:
$$C = USigma V^T$$
其中C是以词为行,文档为列的矩阵,设一共有t行d列, 矩阵的元素为词项的TF-IDF值。然后把 $Sigma$ 的r个对角元素的前k个保留(最大的k个保留), 后面最小的r-k个奇异值置0, 得到 $Sigma_k$ ;最后计算一个近似的分解矩阵
$$C_k = USigma_kV^T$$
$C_k$ 在最小二乘意义下是C的最佳逼近。由于 $Sigma_k$ 最多包含k个非零元素,所以 $C_k$ 的秩不超过k。通过在SVD分解近似,我们将原始的向量转化成一个低维隐含语义空间,起到了特征降维的作用。每个奇异值对应的是每个“语义”维度的权重,将不太重要的权重置为0,只保留最重要的维度信息,去掉一些信息 “nosie”,因而可以得到文档的一种更优表示形式。
LSA的优缺点
- 优点
1)低维空间表示可以刻画同义词,同义词会对应着相同或相似的主题。
2)降维可去除部分噪声,是特征更鲁棒。
3)充分利用冗余数据。
4)无监督/完全自动化。
5)与语言无关。
- 缺点
1)LSA可以处理向量空间模型无法解决的一义多词(synonymy)问题,但不能解决一词多义(polysemy)问题。因为LSA将每一个词映射为潜在语义空间中的一个点,也就是说一个词的多个意思在空间中对于的是同一个点,并没有被区分。
2)SVD的优化目标基于L-2 norm 或者 Frobenius Norm 的,这相当于隐含了对数据的高斯分布假设。而 term 出现的次数是非负的,这明显不符合 Gaussian 假设,而更接近 Multi-nomial分布。(需要进一步研究为什么)
3)特征向量的方向没有对应的物理解释。
4)SVD的计算复杂度很高,而且当有新的文档来到时,若要更新模型需重新训练。
5)没有刻画term出现次数的概率模型。
6)对于count vectors 而言,欧式距离表达是不合适的(重建时会产生负数)。
7)维数的选择是ad-hoc的。
8)LSA具有词袋模型的缺点,即在一篇文章,或者一个句子中忽略词语的先后顺序。
9)LSA的概率模型假设文档和词的分布是服从联合正态分布的,但从观测数据来看是服从泊松分布的。因此LSA算法的一个改进PLSA使用了多项分布,其效果要好于LSA。
3.3 pLSA 潜在语义索引概率模型
尽管基于SVD的LSA取得了一定的成功,但是其缺乏严谨的数理统计基础,而且SVD分解非常耗时。Hofmann在SIGIR’99上提出了基于概率统计的PLSA模型,并且用EM算法学习模型参数。PLSA的概率图模型如下:
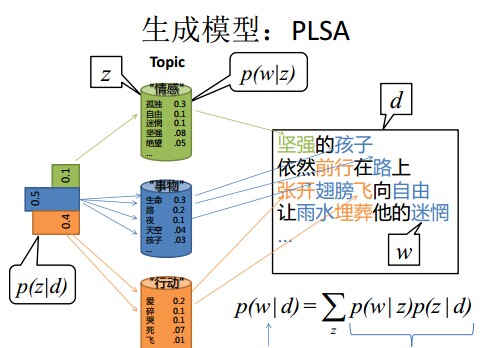

其中D代表文档,Z代表隐含类别或者主题,W为观察到的单词,$P(d_i)$表示单词出现在文档的概率,$P(z_k|d_i) $表示文档$d_i$中出现主题$z_k$下的单词的概率,$P(w_j|z_k)$给定主题$z_k$出现单词$w_j$的概率。并且每个主题在所有词项上服从Multinomial分布,每个文档在所有主题上服从Multinomial 分布。整个文档的生成过程是这样的:
(1) 以$P(d_i)$的概率选中文档$d_i$;
(2) 以$P(z_k|d_i)$的概率选中主题$z_k$;
(3) 以$P(w_j|z_k)$的概率产生一个单词$w_j$。
我们可以观察到的数据就是$(d_i, w_j)$对,而$z_k$是隐含变量。$(d_i, w_j)$的联合分布为:
$$P(d_i,w_j) = P(d_i)P(w_j|d_i), P(w_j|d_i) = sum_{k = 1}^{K}P(w_j|z_k)P(z_k|d_i)$$
而$P(z_k|d_i)$和 $P(w_j|z_k)$分别对应了两组Multinomial分布,我们需要估计这两组分布的参数,一般是用EM算法来估算出pLSA的参数。关于EM算法可以详见从EM算法到GMM模型一文。在此不做推导证明,只列出最终答案:
$$P(w_j|z_k) = frac{sum_{i = 1}^{N}n(d_i,w_j)P(z_k|d_i,wj)}{sum_{m = 1}^{M}{sum_{i = 1}^{N}n(d_i,w_j)P(z_k|d_i,w_m)}}$$
$$P(z_k|d_i) = frac{sum_{j = 1}^{M}n(d_i,w_j)P(z_k|d_i,wj)}{n(d_i)}$$
如此不断在E-step和M-step中迭代,直到满足终止条件。(具体的参考过程可以详见这篇博文)
pLSA将文档中的每个词建模为一个来自混合模型的样本。这个混合模型中的成分是可以被看作“主题”的多项式随机变量。因此每个词都是由单一一个主题产生的,文档中不同的词语可以由不同的主题产生的。每篇文档可以表示为各种主题按照一定比例的混合,成为主题集下的分布。尽管 Hofmann 的成果对于主题概率模型是具有启发性的,但是在 pLSA 模型中,Hofman 仅仅将文档——主题、主题——词的分布视为参数而非随机变量。这使得模型中的参数数目和语料库呈线性关系,最终会导致由于语料库的增大导致过拟合,此外其也缺乏对训练集以外的文档的理论支持。
3.4 LDA (Latent Dirichlet Allocation)
David Blei在2003年提出了LDA(Latent Dirichlet Allocation)的概念,对pLSA模型进行了贝叶斯拓展,利用一种层级贝叶斯模型构建了LDA模型,通过把模型的参数看作随机变量,引入控制参数的参数,实现模型概率化,避免同pLSA那样随着语料库的增大而出现过拟合现象。
自从LDA的概念提出以来,主题模型已经在诸多文本挖掘的领域取得了令人瞩目的成果。主题概率模型不同于以往的空间向量模型(以TF-IDF为例)和语言模型(n-gram 等),它通过主题在词上的概率分布将主题引入文档中,再将文档视为主题的概率分布,从而分析出文档内潜在的主题。主题概率模型的优越性不仅仅体现在其能够分析出文档中的潜在主题,更在于通过主题概率模型,我们能够显著地降低文档特征的维度。相比较于TFIDF中词→文档,主题概率模型通过词→主题→文档将词与文档隔离开,由于主题个数远远小于词数,实现降维的过程。这种显著的降维可以使得针对大数据的分析操作有了实践基础,拥有了更低的训练模型成本。同时更低的维度也将数据自身的噪声影响降得更低,使得训练的结果更加优秀。
参考
https://www.jiqizhixin.com/graph/technologies/e49b21d8-935a-4da6-910d-504c79b9785f
https://www.dazhuanlan.com/2019/10/27/5db4ef2bd0fee/