人工智能必备数学知识学习笔记5：向量的高级话题

• 规范化和单位向量

 

 

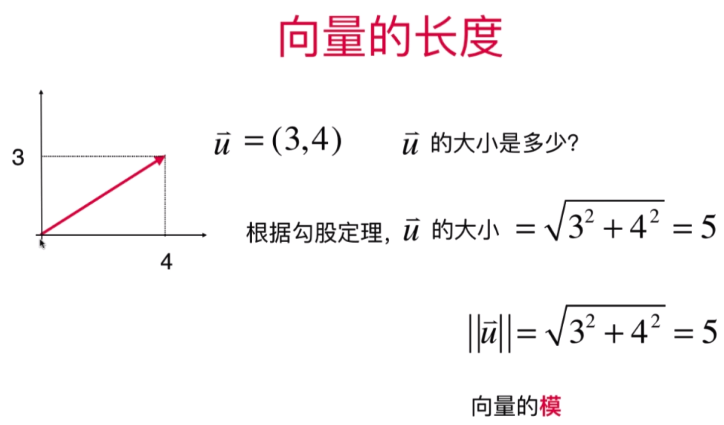
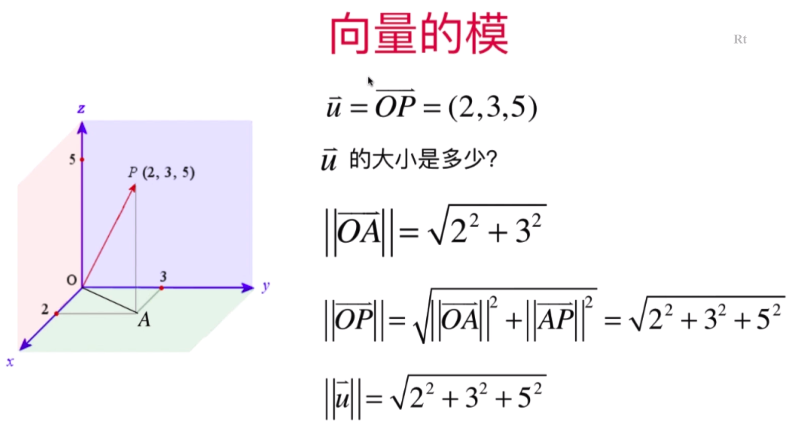
 单位向量：表示向量长度（向量模的最小组成单元）的单位

 

 

 

 代码实现：

　　　　

 1.在 _global.py中编写代码：

 

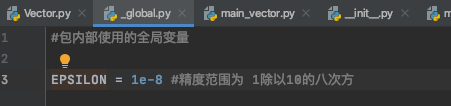
 2.在Vector.py编写代码

#向量类
#__values() 与 _values()区别更多体现在继承上，如果是在类的内部使用时官方建议使用_values()发方法
from ._global import EPSILON
import math


class Vector:

    def __init__(self,lst):
        self._values = list(lst)#将数组赋值给向量类中(注：使用list方法将列表lst复制一份保证他的不被外界调用时修改)

    #零向量类方法：参数1：为当前的类(cls) 参数2：维度(dim)  返回dim维的零向量
    @classmethod
    def zero(cls,dim):
        return cls([0] * dim)

    #返回向量的模(向量长度):
    def norm(self):
        return math.sqrt(sum(e**2 for e in self))#sqrt()方法为开平方根，sum()求和方法，e**2 e的平方

    #返回向量的单位向量
    def normalize(self):
        if self.norm() < EPSILON:  #此处判断一个精度范围(该精度范围调用内部自定义全局变量文件 _global.py)（由于浮点数计算机含有误差所以无法使用 == 0 的操作）
            raise ZeroDivisionError("Normalize error! norm is zero.") #考虑零向量时报此处异常即可
        #方案一：return Vector(1/self.norm() * [e for e in self])#循环遍历向量中的每个元素分别除以该向量的模即为单位向量
        #方案二：return 1/self.norm() * Vector(self._values)#当前向量除以模即为单位向量
        return Vector(self._values) / self.norm()

    #向量加法，返回结果向量
    def __add__(self, another):
        # assert判断传入的向量维度是否相等
        assert len(self) == len(another),
              "Error in adding. Length of vectors must be same."
        return Vector([a+b for a,b in zip(self,another)])#使用zip()方法将两个向量取出来

    # 向量减法
    def __sub__(self, another):
        assert len(self) == len(another), 
            "Error in adding. Length of vectors must be same."
        return Vector([a - b for a, b in zip(self, another)])

    # 向量乘法(数乘数组)，返回数量乘法的结果向量：self * k
    def __mul__(self, k):
        return Vector([k * e for e in self])

    # 向量乘法(数组乘数)，返回数量乘法的结果向量：k * self
    def __rmul__(k, self):
        return k * self #此处直接调用的是上方的乘法函数

    # 向量除法:返回数量除法的结果向量 self / k
    def __truediv__(self, k):
        return (1 / k) * self

    #返回向量取正的结果向量
    def __pos__(self):
        return 1 * self

    # 返回向量取负的结果向量
    def __neg__(self):
        return -1 * self

    #返回向量迭代器（当有迭代器时，zip()方法中就不用再次传入两个向量数组，直接传入向量对象即可<zip(self._values,another._values)>）
    def __iter__(self):
        return self._values.__iter__()

    #取向量的index个元素
    def __getitem__(self, index):
        return self._values[index]

    #返回向量的长度（有多少个元素）
    def __len__(self):
        return len(self._values)

    # 向量展示（系统调用）
    def __repr__(self):
        return "Vector({})".format(self._values)

    # 向量展示（用户调用）
    def __str__(self):
        return "({})".format(", ".join(str(e) for e in self._values))#通过遍历 self.__values 将e转成字符串通过逗号加空格来链接放入大括号中

# u = Vector([5,2])
# print(u)

3.在main_vector.py展示中编写：

from playLA.Vector import Vector

if __name__ == "__main__":

    vec = Vector([5,2])
    print(vec)
    print(len(vec))#打印向量的维度
    print("vec[0] = {}, vec[1] = {}".format(vec[0],vec[1]))

    #向量加法
    vec2 = Vector([3,1])
    print("{} + {} = {}".format(vec,vec2,vec+vec2))
    #向量减法
    print("{} - {} = {}".format(vec, vec2, vec - vec2))
    #向量乘法(向量乘以数)
    print("{} * {} = {}".format(vec,3,vec * 3))
    # 向量乘法(数乘以向量)
    print("{} * {} = {}".format(3, vec, 3 * vec))
    # 向量取正
    print("+{} = {}".format(vec, +vec))
    # 向量取负
    print("-{} = {}".format(vec, -vec))

    #零向量
    zero2 = Vector.zero(2)
    print(zero2)
    #向量加上零向量
    print("{} + {} = {}".format(vec, zero2, vec + zero2))

    #向量的模
    print("norm({}) = {}".format(vec,vec.norm()))
    print("norm({}) = {}".format(vec2,vec2.norm()))
    print("norm({}) = {}".format(zero2, zero2.norm()))

    #单位向量
    print("normalize({}) is {}".format(vec,vec.normalize()))
    print(vec.normalize().norm())#单位向量的模(长度)基本为数字1
    print("normalize({}) is {}".format(vec2, vec2.normalize()))
    print(vec2.normalize().norm())  # 单位向量的模(长度)基本为数字1（计算机中会有误差0.9999...）
    #print(zero2.normalize())
    #捕捉异常 ZeroDivisionError
    try:
        zero2.normalize()
    except ZeroDivisionError:
        print("Cannot normalize zero vector {}".format(zero2))

4.运行main_vector.py结果为：

/Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=57619
import sys; print('Python %s on %s' % (sys.version, sys.platform))
sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra'])
PyDev console: starting.
Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 
[Clang 6.0 (clang-600.0.57)] on darwin
runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_vector.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra')
(5, 2)
2
vec[0] = 5, vec[1] = 2
(5, 2) + (3, 1) = (8, 3)
(5, 2) - (3, 1) = (2, 1)
(5, 2) * 3 = (15, 6)
3 * (5, 2) = (15, 6)
+(5, 2) = (5, 2)
-(5, 2) = (-5, -2)
(0, 0)
(5, 2) + (0, 0) = (5, 2)
norm((5, 2)) = 5.385164807134504
norm((3, 1)) = 3.1622776601683795
norm((0, 0)) = 0.0
normalize((5, 2)) is (0.9284766908852593, 0.3713906763541037)
1.0
normalize((3, 1)) is (0.9486832980505138, 0.31622776601683794)
0.9999999999999999
Cannot normalize zero vector (0, 0)

---

---

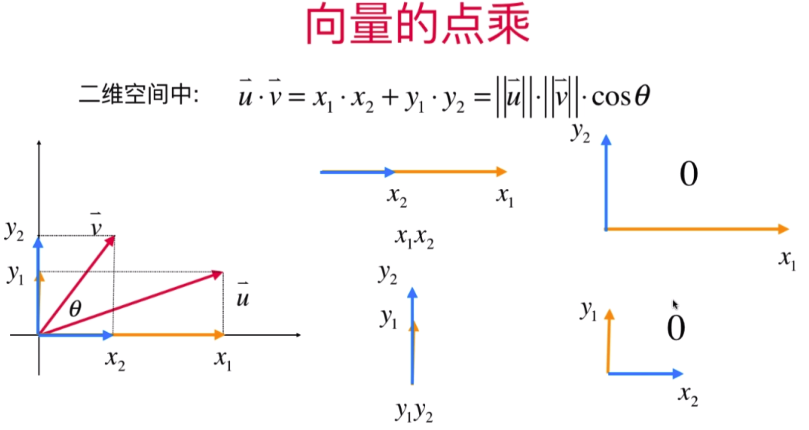
• 向量的点乘

 

 

 

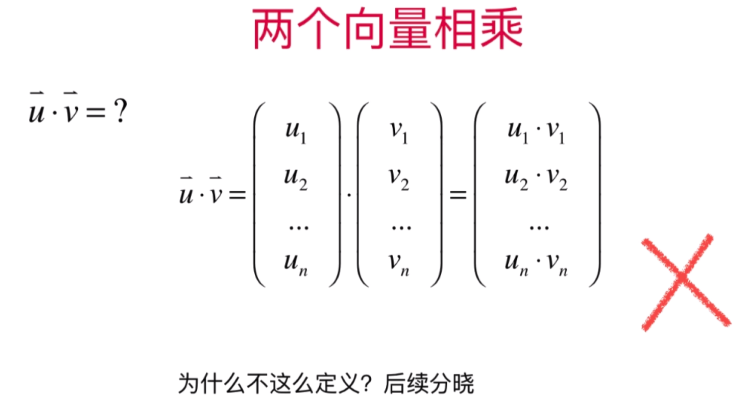
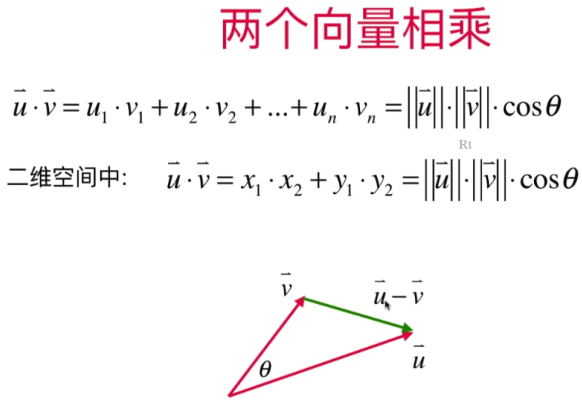
 余弦定理：

 多维两个向量点乘：

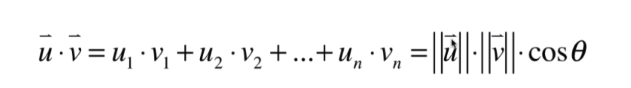
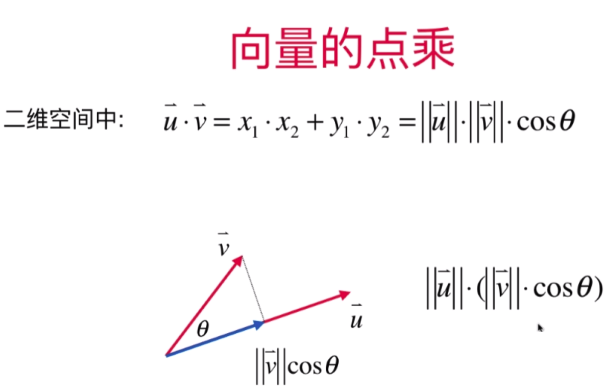
 向量点乘的直观理解：将向量V投影到u向量上长度：将两个向量的指向相同后再相乘

 

 

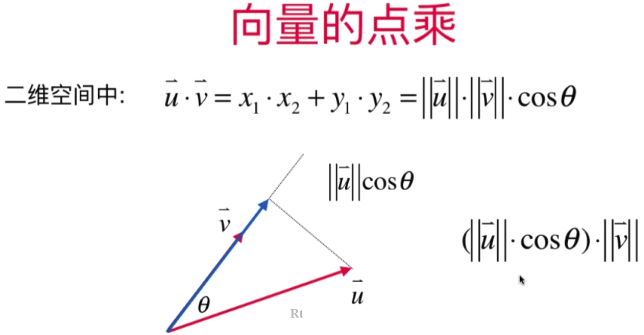
 代码实现：

1.在Vector.py编写代码

#向量类
#__values() 与 _values()区别更多体现在继承上，如果是在类的内部使用时官方建议使用_values()发方法
from ._global import EPSILON
import math


class Vector:

    def __init__(self,lst):
        self._values = list(lst)#将数组赋值给向量类中(注：使用list方法将列表lst复制一份保证他的不被外界调用时修改)

    #零向量类方法：参数1：为当前的类(cls) 参数2：维度(dim)  返回dim维的零向量
    @classmethod
    def zero(cls,dim):
        return cls([0] * dim)

    #返回向量的模(向量长度):
    def norm(self):
        return math.sqrt(sum(e**2 for e in self))#sqrt()方法为开平方根，sum()求和方法，e**2 e的平方

    #返回向量的单位向量
    def normalize(self):
        if self.norm() < EPSILON:  #此处判断一个精度范围(该精度范围调用内部自定义全局变量文件 _global.py)（由于浮点数计算机含有误差所以无法使用 == 0 的操作）
            raise ZeroDivisionError("Normalize error! norm is zero.") #考虑零向量时报此处异常即可
        #方案一：return Vector(1/self.norm() * [e for e in self])#循环遍历向量中的每个元素分别除以该向量的模即为单位向量
        #方案二：return 1/self.norm() * Vector(self._values)#当前向量除以模即为单位向量
        return Vector(self._values) / self.norm()

    #向量加法，返回结果向量
    def __add__(self, another):
        # assert判断传入的向量维度是否相等
        assert len(self) == len(another),
              "Error in adding. Length of vectors must be same."
        return Vector([a+b for a,b in zip(self,another)])#使用zip()方法将两个向量取出来

    # 向量减法
    def __sub__(self, another):
        #判断维度相等
        assert len(self) == len(another), 
            "Error in adding. Length of vectors must be same."
        return Vector([a - b for a, b in zip(self, another)])

    #向量点乘(向量之间相乘)：返回结果标量
    def dot(self,another):
        #判断维度相等
        assert len(self) == len(another), 
            "Error in dot product. Length of vectors must be same."
        return sum(a * b for a,b in zip(self,another))# 方法zip()将两组向量配成对应位置的数据对

    # 向量数量乘法(数乘数组)，返回数量乘法的结果向量：self * k
    def __mul__(self, k):
        return Vector([k * e for e in self])

    # 向量数量乘法(数组乘数)，返回数量乘法的结果向量：k * self
    def __rmul__(k, self):
        return k * self #此处直接调用的是上方的乘法函数

    # 向量除法:返回数量除法的结果向量 self / k
    def __truediv__(self, k):
        return (1 / k) * self

    #返回向量取正的结果向量
    def __pos__(self):
        return 1 * self

    # 返回向量取负的结果向量
    def __neg__(self):
        return -1 * self

    #返回向量迭代器（当有迭代器时，zip()方法中就不用再次传入两个向量数组，直接传入向量对象即可<zip(self._values,another._values)>）
    def __iter__(self):
        return self._values.__iter__()

    #取向量的index个元素
    def __getitem__(self, index):
        return self._values[index]

    #返回向量的长度（有多少个元素）
    def __len__(self):
        return len(self._values)

    # 向量展示（系统调用）
    def __repr__(self):
        return "Vector({})".format(self._values)

    # 向量展示（用户调用）
    def __str__(self):
        return "({})".format(", ".join(str(e) for e in self._values))#通过遍历 self.__values 将e转成字符串通过逗号加空格来链接放入大括号中

# u = Vector([5,2])
# print(u)

2.在main_vector.py展示中编写：

from playLA.Vector import Vector

if __name__ == "__main__":

    vec = Vector([5,2])
    print(vec)
    print(len(vec))#打印向量的维度
    print("vec[0] = {}, vec[1] = {}".format(vec[0],vec[1]))

    #向量加法
    vec2 = Vector([3,1])
    print("{} + {} = {}".format(vec,vec2,vec+vec2))
    #向量减法
    print("{} - {} = {}".format(vec, vec2, vec - vec2))
    #向量乘法(向量乘以数)
    print("{} * {} = {}".format(vec,3,vec * 3))
    # 向量乘法(数乘以向量)
    print("{} * {} = {}".format(3, vec, 3 * vec))
    # 向量取正
    print("+{} = {}".format(vec, +vec))
    # 向量取负
    print("-{} = {}".format(vec, -vec))

    #零向量
    zero2 = Vector.zero(2)
    print(zero2)
    #向量加上零向量
    print("{} + {} = {}".format(vec, zero2, vec + zero2))

    #向量的模
    print("norm({}) = {}".format(vec,vec.norm()))
    print("norm({}) = {}".format(vec2,vec2.norm()))
    print("norm({}) = {}".format(zero2, zero2.norm()))

    #单位向量
    print("normalize({}) is {}".format(vec,vec.normalize()))
    print(vec.normalize().norm())#单位向量的模(长度)基本为数字1
    print("normalize({}) is {}".format(vec2, vec2.normalize()))
    print(vec2.normalize().norm())  # 单位向量的模(长度)基本为数字1（计算机中会有误差0.9999...）
    #print(zero2.normalize())
    #捕捉异常 ZeroDivisionError
    try:
        zero2.normalize()
    except ZeroDivisionError:
        print("Cannot normalize zero vector {}".format(zero2))

    #向量点乘(向量乘以向量)
    print(vec.dot(vec2))

3.运行main_vector.py结果为：

/Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=58247
import sys; print('Python %s on %s' % (sys.version, sys.platform))
sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra'])
PyDev console: starting.
Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 
[Clang 6.0 (clang-600.0.57)] on darwin
>>> runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/main_vector.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra')
(5, 2)
2
vec[0] = 5, vec[1] = 2
(5, 2) + (3, 1) = (8, 3)
(5, 2) - (3, 1) = (2, 1)
(5, 2) * 3 = (15, 6)
3 * (5, 2) = (15, 6)
+(5, 2) = (5, 2)
-(5, 2) = (-5, -2)
(0, 0)
(5, 2) + (0, 0) = (5, 2)
norm((5, 2)) = 5.385164807134504
norm((3, 1)) = 3.1622776601683795
norm((0, 0)) = 0.0
normalize((5, 2)) is (0.9284766908852593, 0.3713906763541037)
1.0
normalize((3, 1)) is (0.9486832980505138, 0.31622776601683794)
0.9999999999999999
Cannot normalize zero vector (0, 0)
17

---

---

•  向量点乘的意义 

 

 

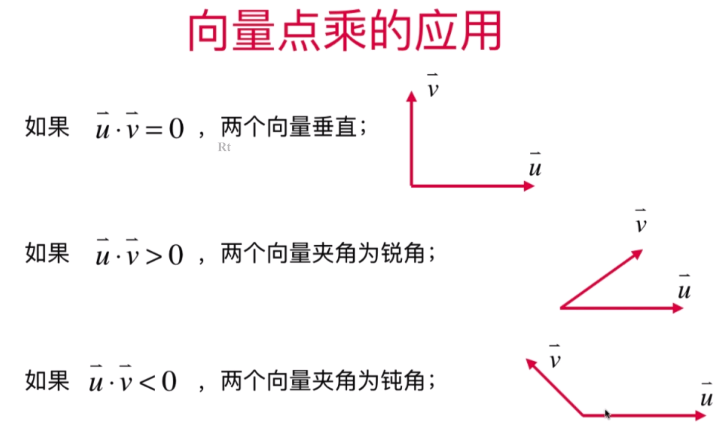
引申：推荐系统算法基础

 

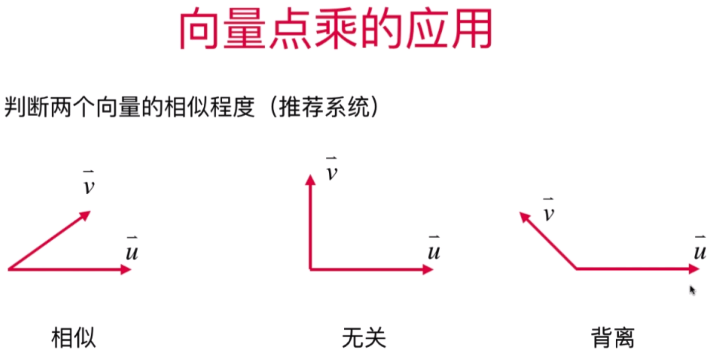
 几何应用：投影点的方向可以表示为单位向量，所以投影点坐标为单位向量乘以一个投影点的距离

---

---

• numpy的使用（numpy是线性代数库）

1.创建main_numpy_vector.py文件

 2. 文件 main_numpy_vector.py 编写代码

import numpy as np
if __name__ == "__main__":
    #查看 数学库 numpy 的版本号
    print(np.__version__)

    lst = [1,2,3]
    lst[0] = "Linear Algebra"#线性代数的英文
    print(lst)

    #使用numpy中的向量
    vec = np.array([1,2,3])
    print(vec)
    # vec[0] = 666
    # print(vec)

    #np.array的创建 (参数1：维度数 参数2：每个维度的元素值)
    print(np.zeros(5))
    print(np.ones(5))
    print(np.full(5,666))

    #np.array的基本属性
    print(vec)
    print("size=",vec.size)#向量有多少元素（维度数）
    print("size=",len(vec))
    print(vec[0])#第一个元素值
    print(vec[-1])#最后一个元素值
    print(vec[0:2])#切片语法，参数1：从哪开始，参数2：步长
    print(type(vec[0:2]))#该切片的向量的类

    #np.array的基本运算
    vec2 = np.array([4,5,6])
    print("{} + {} = {}".format(vec,vec2,vec + vec2))#向量加法
    print("{} - {} = {}".format(vec, vec2, vec - vec2))  # 向量减法
    print("{} * {} = {}".format(2, vec, 2 * vec))  # 向量乘法(数乘以向量)
    print("{} * {} = {}".format(vec, 2, vec * 2))  # 向量乘法(向量乘以数)
    print("{} * {} = {}".format(vec, vec2, vec * vec2))  # 向量乘法(向量与向量对应元素相乘-但无数学意义)
    print("{}.dot({}) = {}".format(vec, vec2, vec.dot(vec2)))  # 向量点乘(向量与向量点乘)

    #np.linalg 为numpy中线性代数模块（"Linear Algebra"的缩写）
    print(np.linalg.norm(vec))# 向量的模（向量的长度）
    print(vec / np.linalg.norm(vec))# 单位向量
    print(np.linalg.norm(vec / np.linalg.norm(vec)))# 单位向量的模

    #numpy涉及零向量的单位向量时会报错，需要自行处理
    # zero3 = np.zeros(3)
    # zero3 / np.linalg.norm(zero3)

 3. 运行文件 main_numpy_vector.py 结果为：

/Users/liuxiaoming/PycharmProjects/LinearAlgebra/venv/bin/python /Applications/PyCharm.app/Contents/plugins/python/helpers/pydev/pydevconsole.py --mode=client --port=58662
import sys; print('Python %s on %s' % (sys.version, sys.platform))
sys.path.extend(['/Users/liuxiaoming/PycharmProjects/LinearAlgebra'])
PyDev console: starting.
Python 3.8.2 (v3.8.2:7b3ab5921f, Feb 24 2020, 17:52:18) 
[Clang 6.0 (clang-600.0.57)] on darwin
runfile('/Users/liuxiaoming/PycharmProjects/LinearAlgebra/playLA/main_numpy_vector.py', wdir='/Users/liuxiaoming/PycharmProjects/LinearAlgebra/playLA')
1.19.1
['Linear Algebra', 2, 3]
[1 2 3]
[0. 0. 0. 0. 0.]
[1. 1. 1. 1. 1.]
[666 666 666 666 666]
[1 2 3]
size= 3
size= 3
1
3
[1 2]
<class 'numpy.ndarray'>
[1 2 3] + [4 5 6] = [5 7 9]
[1 2 3] - [4 5 6] = [-3 -3 -3]
2 * [1 2 3] = [2 4 6]
[1 2 3] * 2 = [2 4 6]
[1 2 3] * [4 5 6] = [ 4 10 18]
[1 2 3].dot([4 5 6]) = 32
3.7416573867739413
[0.26726124 0.53452248 0.80178373]
1.0