在数值线性代数中,QR因子分解的思想比其他所有算法的思想更为重要[1]。
--Lloyd N. Trefethen & David Bau, lll
在给出QR因子分解定理之前,先回顾两个知识点,一是正交矩阵(它的重要性在数值线性代数中似乎怎么强调都不过分),二是线性代数中的 Gram-Schmidt 正交化算法,这个算法是把一组线性无关的向量组alpha_1, ... ,alpha_n 转化为相互正交的向量组 q_1, ... ,q_n的方法,且有下列表达形式
q_k = a1*alpha_1+...+ak*alpha_k, k=1,...n
令A=[alpha_1, ... ,alpha_n], Q=[q_1, ... ,q_n], 则上式可以写成 Q = A*T, 其中T是一个上三角形矩阵。假设 A 是满秩的,则 T 具有逆矩阵,不妨记成R,在等式两边分别右乘矩阵R, 则可以得到A=QR。
针对一般矩阵,则有下列的 QR 因子分解定理:对于任意m*n维的实矩阵 A(不妨假设m>=n),有相应的QR因子分解,即A=QR, 其中 Q 是具有正交列的m*m矩阵,R 是m*n的上三角矩阵,如图1.(a) 所示[1]。

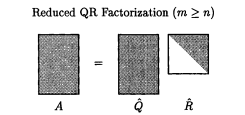
图1.(a) 完全 QR 因子分解 图1.(b) 约化 QR 因子分解
如果将矩阵R的零行以及矩阵Q中不起作用的列去掉的话,则A=Q1R1,这里 Q1 具有列正交的m*n维矩阵,R1 是n*n的上三角矩阵,这种形式称为约化QR因子分解,如图1.(b) 所示,相应地,图1.(a)的分解形式称为完全QR因子分解。
既然矩阵有QR分解,那么一个自然的问题是给定一个具体的矩阵,如何求它的QR因子分解呢?实际上,从理论的角度来看,Gram-Schmidt正交化给出了一种数值实现的方法。不过,由于舍入误差的影响,该方法会在计算过程中损失正交性,即理论上求得的向量之间是相互正交的,但是数值求得的向量的正交性很差。因此,在求解QR因子分解中,传统的Gram-Schmidt正交化方法基本不用,而改用修正的Gram-Schmidt正交化方法。后者和前者相比,得到的向量的正交性更好,后者可以看成是一系列正交投影算子的作用,所谓 P 是一个正交投影算子,即它满足P*P=P(投影算子)以及P'=P。做个不恰当的类比,把向量之间的正交性看成是总体误差的话,前者只在最后一步进行了误差校正,而后者在每一步都进行误差校正,自然地,经过这样的处理,后者的误差显然比前者小。
观察 QR 因子分解,不管是传统还是修正的Gram-Schmidt正交化过程,它们通过对矩阵施行三角化(右乘上三角阵),来依次求出 Q 的每一列,在[2]中称作三角形对角化。另一种实现的方式是,通过构造一系列的正交矩阵(正交矩阵的乘积依旧是正交矩阵),来依次求出 R 的每一列(由于正交矩阵的转置即为它的逆,所以相应的Q也很容易求得),这种方法称为对角三角形化,如图2所示:
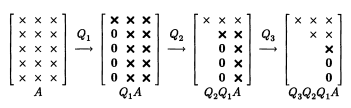
图2. 对角三角形化QR因子分解
下面的问题就是 Q 如何构造呢?点解,通过Householder变换或者Givens变换。先说Householder变换,参见图3,它将一个向量变换到只有前面数个坐标值非零,而后面的坐标值均为零的向量(参见图2,将A通过Q1变换后,A的第一列向量发生了改变)v,那么此时 Householder 变换为 Q1= I-2(vv')/(v'v),其中v=-sign(x1)||x||e1,x是A的第一列,x1是向量x的第一个元素值,e1是第一个元素为1的单位向量(注1)。由于矩阵(vv')/(v'v)的秩为1,所以该变换也被称为单位阵的秩1修正。至于 Q2 以及 Q3 的构造,以 Q2 为例,考虑下列分块矩阵Q2=diag(I1, I2-2(v1v1')/(v1'v1)),其中v1是 Q1A 的第二列向量去掉第一个元素剩下的向量经过转换得到的,容易验证 Q2Q1A 就是图2中的结果。Givens 变换是一个旋转变换,每次将矩阵中的一个元素修改为0,与 Householder 变换相对应,它是单位矩阵的秩2修正。 
图3. Householder变化示意图
总结一下,实现矩阵QR分解的方法有三角形对角化(修正的Gram-Schmidt算法,简称MGS)以及对角三角形化(Householder三角形化)。从数值结果的精度来看,尤其是正交矩阵之间的正交性来分析,后者比前者更好一些(注2),而Givens三角形化和Householder三角形化的结果相似[2]。但是,MGS可以根据需要在中间的某一步进行终止,而Householder三角形化却不具备这一特点。
拉拉杂杂说了这么多,有一个问题却没有提及,那就是 QR 方法有什么用途呢?点解。矩阵的特征值问题(除了使用QR算法外,还使用了逆迭代以及位移技术,因此QR算法被称为最复杂的算法),最小二乘法[3]以及多项式求根问题[4]中都有它的身影,而高斯消去法中涉及到的变换矩阵的某些性质在 MGS 中也出现过。
相应的Matlab命令: qr
注1. 从数学推导的角度来看,v的符号可以取为sign(x1),之所以取成负数的形式,原因是为了避免两个相近的数字相减的情形,而这种情形很容易造成数值结果精度的很大损失。
注2. 简略地说,Householder三角化得到的正交矩阵的正交性和机器精度成正比,而MGS的正交矩阵的正交性和机器精度与矩阵A的条件数的乘积成正比。
注3. 文中涉及到的图片均取自参考资料[1]。
参考文献:
[1] 数值线性代数 Chap7-11,L N. Trefethen,David Bau, lll 著,陆金甫,关治译,人民邮电出版社,2006年
[2] 应用数值线性代数,J W. Demmel 著,王国荣译,人民邮电出版社,2007年
[3] 矩阵计算(第三版),Gene H.Golub,