1319. 连通网络的操作次数
Difficulty: 中等
用以太网线缆将 n 台计算机连接成一个网络,计算机的编号从 0 到 n-1。线缆用 connections 表示,其中 connections[i] = [a, b] 连接了计算机 a 和 b。
网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。
给你这个计算机网络的初始布线 connections,你可以拔开任意两台直连计算机之间的线缆,并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能,则返回 -1 。
示例 1:
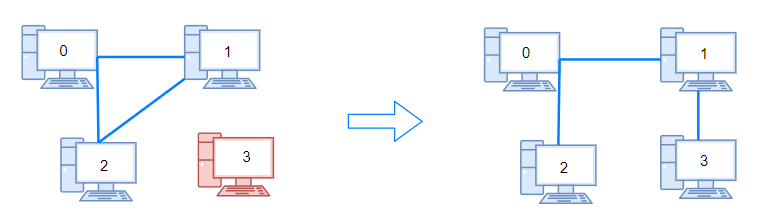
输入:n = 4, connections = [[0,1],[0,2],[1,2]]
输出:1
解释:拔下计算机 1 和 2 之间的线缆,并将它插到计算机 1 和 3 上。
示例 2:
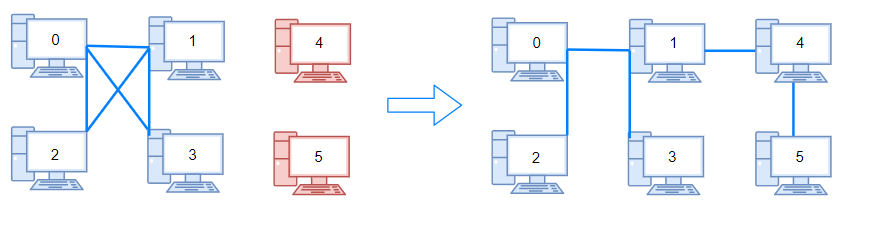
输入:n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出:2
示例 3:
输入:n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
输出:-1
解释:线缆数量不足。
示例 4:
输入:n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]
输出:0
提示:
1 <= n <= 10^51 <= connections.length <= min(n*(n-1)/2, 10^5)connections[i].length == 20 <= connections[i][0], connections[i][1] < nconnections[i][0] != connections[i][1]- 没有重复的连接。
- 两台计算机不会通过多条线缆连接。
Solution
思路:使用并查集查看有多少个电脑是独立的。题意转化为如何让图变成连通图,即没有孤立的点或子图。首先,当边的个数少于点的个数-1时,那么至少有一个点不是连通的,此时返回-1。每个不连通的点或图,只要加一个边就能连通,因此,只要知道有不连通的点或图的个数,那么需要该个数减一的边就可以将他们全部连通。
Language: java
class Solution {
public int makeConnected(int n, int[][] connections) {
if(n > connections.length + 1) return -1;
if(n == 1) return 0;
UnionFind uf = new UnionFind(n);
for(int i=0; i<connections.length; i++){
uf.merge(connections[i][0], connections[i][1]);
}
Set<Integer> set = new HashSet<>();
for(int i=0; i<n; i++){
set.add(uf.find(i));
}
return set.size()-1;
}
class UnionFind{
int[] parent;
public UnionFind(int n){
parent = new int[n];
for(int i=0; i<n; i++) parent[i] = i;
}
public int find(int i){
return i == this.parent[i] ? i : (this.parent[i] = find(this.parent[i]));
}
public void merge(int i, int j){
this.parent[find(j)] = find(i);
}
}
}