第75课 图的遍历（深度优先遍历DFS）

A开始有3条分支，首先选择B走到底ABEG，走不通的时候回退走另外一条GBCFD

（1）A开始分叉选择一条边走，走到B分叉，再选择一条边E开始走，继续到G没有边了，然后回退到E看E有没有其他边，没有再回退到B，B 有其他边，选择C

　　　　只要在当前的顶点上面，有边可以走到其他顶点，那么就深入放入走下去

原材料：栈

 （1）

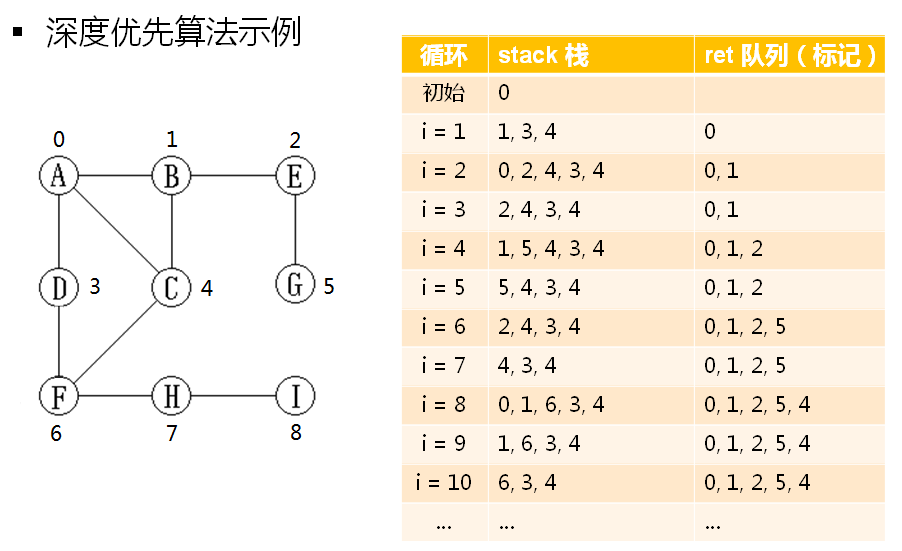
从i顶点开始对图进行深度优先遍历

（1）原材料 :栈 stack（保存顶点）   队列 return  访问标记数组 visited 

（2）初始值状态每个顶点都没有标记访问  visited = { false }

（3）初始顶点 i 压入栈顶

（4）判断栈是否为空  循环  ----------也就是栈内是否还有顶点

（5）没有------取出栈顶顶点  v=stack.top();  stack.pop();

（6）v判断取出的顶点v是否访问  visited[v]

（7）没有访问-----将顶点 v 的邻接顶点取出来，压入栈中 

（8）将v顶点取出压入 reture 队列，将v标记为以访问

（9）判断栈内是否还有元素 --------  循环找下一个栈顶

（10）判断访问状态   访问了----扔出去  没有 流程循环

　　队列 return---------保存的是深度优先访问下的顶点次序

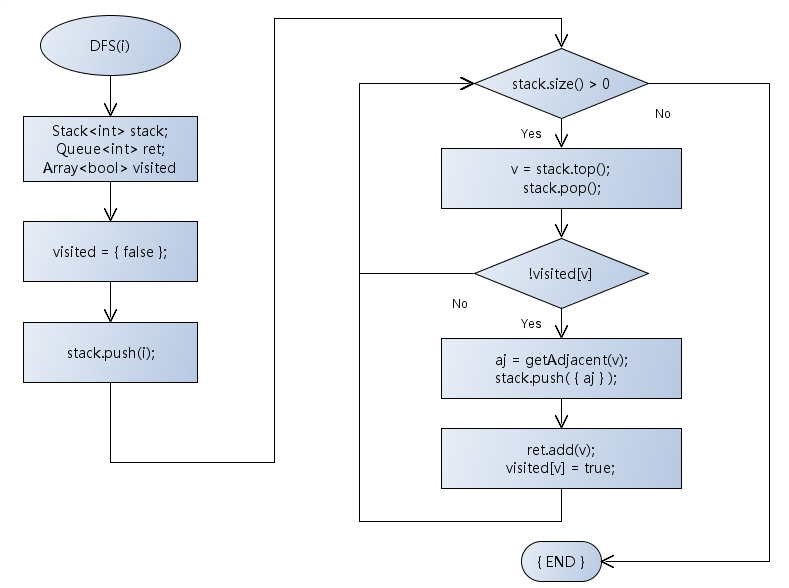
添加DFS函数：

#ifndef GRAPH_H
#define GRAPH_H

#include "Object.h"
#include "SharePointer.h"
#include "DynamicArray.h"
#include "LinkQueue.h"
#include "LinkStack.h"

using namespace std;
namespace DTLib
{

    /* 设置边的数据结构，用于邻接链表 */
    template < typename E >
    struct Edge : public Object
    {
        int b;  // 起点
        int e;  // 终点
        E data;  // 权值

        Edge(int i = -1, int j = -1)  //构造函数
        {
            b = i;
            e = j;
        }

        Edge(int i, int j, const E& value) //重载函数
        {
            b = i;
            e = j;
            data = value;
        }

        /* 相等和不等不需要对权值进行比价，只比较起始点位置，终止位置，删除顶点操作中查找操作用到,在此处定义了 */
        bool operator == (const Edge<E>& obj)
        {
            return (b == obj.b) && (e == obj.e);  //起点终点相等，边对象相等，不关注权值
        }

        bool operator != (const Edge<E>& obj) 
        {
            return !(*this == obj);
        }

        bool operator < (const Edge<E>& obj)
        {
            return (data < obj.data);  // 权值比较边的大小
        }

        bool operator > (const Edge<E>& obj)
        {
            return (data > obj.data);  // 权值比较边的大小
        }
    };

    /* 抽象类不能够用来继承，能用来定义指针-----------队列转数组 */
    template < typename V, typename E >
    class Graph : public Object
    {
    protected:

        //队列转数组
        template <typename T>
        DynamicArray<T>* toArray(LinkQueue<T>& queue)
        {
            DynamicArray<T>* ret = new DynamicArray<T>(queue.length())   //堆空间申请与队列长度一致的数组对象

            if (ret != NULL)
            {
                for (int i = 0; i < ret->length(); i++, queue.remove())  
                {
                    ret->set(i, queue.front()); //队列中每个数组放在队列中
                }
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "no enough memoty ...");
            }

            return ret;
        }

    public:
        virtual V getVertex(int i) = 0;  // V 表示与顶点相关联的数据类型
        virtual bool getVertex(int i, V& value) = 0;
        virtual bool setVertex(int i, const V& value) = 0;
        virtual SharedPointer< Array<int> > getAdgacent(int i) = 0;
        virtual bool isAdjacent(int i, int j) = 0;//i和j 是否连接，只能在继承中实现
        virtual E getEdge(int i, int j) = 0;// E表示与边相关联的数据类型,得到边上的//权值
        virtual bool getEdge(int i, int j, E& value) = 0;
        virtual bool setEdge(int i, int j, const E& value) = 0;
        virtual bool removeEdge(int i, int j) = 0;
        virtual int vCount() = 0;
        virtual int eCount() = 0;
        virtual int OD(int i) = 0;
        virtual int ID(int i) = 0;
        virtual int TD(int i)  // 顶点 i 的度，即与顶点 i 相关联的边的数目
        {
            return OD(i) + ID(i);  // 出度加上入度
        }



        /* 判断在当前图中顶点i到顶点j是否邻接*/
        virtual bool isAdjacent(int i, int j) = 0;              
        
        /* 判断当前的有向图是否可以看做无向图*/
        bool asUndirected()                                      
        {
            bool ret = true;

            for (int i = 0; i < vCount(); i++)
            {
                for (int j = 0; j < vCount(); j++)
                {
                    if (isAdjacent(i, j))        //i到j有边，j到i也有边，且i到j，j到i的权值相等
                    {
                        ret = ret && isAdjacent(j, i) && (getEdge(i, j) == getEdge(j, i));
                    }
                }
            }

            return ret;
        }

    

        /*广度优先遍历算法*/
        SharedPointer<Array<int>> BFS(int i)   
        {
            DynamicArray<int>* ret = NULL;  //返回值是数组：保存图中顶点的编号-----
                                        //使用数组原因----通过数组元素次序访问顶点访问先后次序

            if ((0 <= i) && (i < vCount()))   
            {
                LinkQueue<int> q;    //queue队列
                LinkQueue<int> r;    // rerurn 队列-----保存访问过的顶点
                DynamicArray<bool> visited(vCount());   //标记数组：标记顶点是否被访问

                /*初始值设置*/
                for (int i = 0; i < vCount(); i++)
                {
                    visited[i] = false;  //默认每个顶点都没有被访问
                }

                q.add(i);    //顶点加队列queue

                while (q.length()>0)  //循环(queue不为空)
                {
                    int v = q.front();     
                    q.remove();   //取队列头部顶点   

                    if (!visited[i])  //判断顶点是否访问
                    {
                        SharedPointer<Array<int>> aj = getAdgacent(v);    //取v的邻接顶点

                        /*邻接顶点放入Queue队列*/
                        for (int j = 0; j < aj->length(); j++)
                        {
                            q.add(*(aj)[j]);  
                        }

                        r.add(v);       //顶点v压入return队列

                        visited[v] = true;  //标记数组为true表示被访问
                    }
                }
                ret = toArray(r);  //要实现队列转数组,因为返回值是数组
            }
            else
            {
                THROW_EXCEPTION(InvalidParameterException, "index i is invalid ...");
            }

            return ret;
        }

        /*深度优先遍历算法*/---------------------------------------//深度优先算法-------------------------------------------
        SharedPointer<Array<int>> DFS(int i)
        {
            DynamicArray<int>* ret = NULL;  //返回值----数组

            if ((0 <= i) && (i < vCount()))  //顶点合法
            {
                //3个原材料
                LinkStack<int> s;  //栈---保存顶点数据元素
                LinkQueue<int> r;   //队列----保存的是深度优先访问下的顶点次序
                DynamicArray<bool> visited(vCount());   //标记数组-----标记顶点有没有被访问

                for (int j = 0; j < visited.length(); j++)   
                {
                    visited[j] = false;             //标记数组初始化为false，所以顶点都没有被访问
                }

                s.push(i);      //初始顶点i压栈  
                 
                while (s.size() > 0)     //栈内有顶点------一直循环                
                {
                    int v = s.top();   //找栈顶顶点v

                    s.pop();           //弹出栈顶顶点v

                    if (!visited[j])     //判断栈顶顶点有没有被标记
                    {
                        //未被标记访问
                        SharedPointer<Array<int>> aj =  getAdgacent(v);  //取出顶点v的邻接顶点

                        for (int j = aj->length() - 1; j >= 0; j--)
                        {
                            s.push((*aj)[i]);        //顶点v的所有邻接顶点压入栈
                        }

                        r.add(v);             //将顶点v弹出，保存在return队列

                        visited[v] = true;   //标记此时顶点为访问状态---true
                    }
                }

                ret = toArray(r);  //队列转化为数组-------因为返回值是数组
            }
            else
            {
                THROW_EXCEPTION(InvalidParameterException, "index i is invalid ...");
            }
        }
//-------------------------------------------------------------------------------------------------------------------
    
    };
}
#endif // GRAPH_H

测试程序如下：

 1 #include <iostream>
 2 #include "BTreeNode.h"
 3 #include "ListGraph.h"
 4 #include "MatrixGraph.h"
 5 
 6 using namespace std;
 7 using namespace DTLib;
 8 
 9 
10 int main()
11 {
12     MatrixGraph<9, char, int> g;
13     const char* VD = "ABEDCGFHI";
14 
15     for(int i=0; i<9; i++)
16     {
17         g.setVertex(0, VD[i]);
18     }
19 
20     g.setEdge(0, 1, 0);
21     g.setEdge(1, 0, 0);
22 
23     g.setEdge(0, 3, 0);
24     g.setEdge(3, 0, 0);
25 
26     g.setEdge(0, 4, 0);
27     g.setEdge(4, 0, 0);
28 
29     g.setEdge(1, 2, 0);
30     g.setEdge(2, 1, 0);
31 
32     g.setEdge(1, 4, 0);
33     g.setEdge(4, 1, 0);
34 
35     g.setEdge(2, 5, 0);
36     g.setEdge(5, 2, 0);
37 
38     g.setEdge(3, 6, 0);
39     g.setEdge(6, 3, 0);
40 
41     g.setEdge(4, 6, 0);
42     g.setEdge(6, 4, 0);
43 
44     g.setEdge(6, 7, 0);
45     g.setEdge(7, 6, 0);
46 
47     g.setEdge(7, 8, 0);
48     g.setEdge(8, 7, 0);
49 
50     SharedPointer< Array<int> > sa = g.DFS(0);  //深度优先遍历
51 
52     for(int i=0; i<sa->length(); i++)
53     {
54         cout << (*sa)[i] << " ";
55     }
56 
57     cout << endl;
58 
59     return 0;
60 }

结果如下：

 

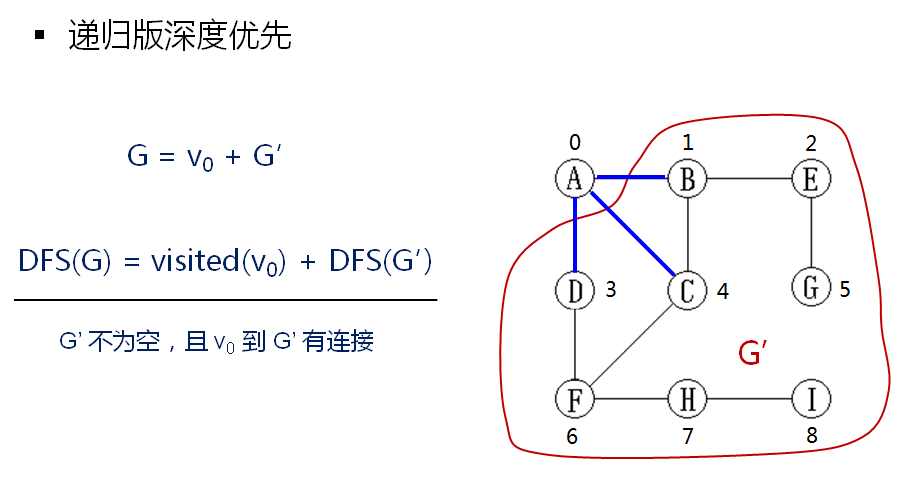
 (1)划分：起始顶点v0 + 剩余部分（原来图的子图）---------------1，先访问起始顶点   2，深度遍历剩余部分子图

深度优先的思想就是二叉树的先序遍历思想。

 （1）graph 深度遍历的图      vex是起始顶点       DFS(graph,vex);   以vex为起始顶点，深度优先遍历graph

（2）vex 没有邻接顶点，访问结束

（3）vex 有邻接顶点 ，也就是vex到子图是有连接的，开始递归

　　　　1，访问起始顶点vex

　　　　2，取邻接顶点 aj

　　　　3，以aj 为新的起始顶点，深度优先遍历图

递归版的深入优先算法如下：

#include <iostream>
#include "BTreeNode.h"
#include "ListGraph.h"
#include "MatrixGraph.h"

using namespace std;
using namespace DTLib;

//二叉树先序遍历图 ----------  递归函数
template < typename V, typename E>
void DFS(Graph<V, E>& g, int v, Array<bool>& visited) 
{
    if( (0 <= v) && (v < g.vCount()) )   //判断顶点v合法
    {
        cout << v << endl;

        visited[v] = true;   //标记当前图起始顶点v 是被访问状态

        SharedPointer< Array<int> > aj = g.getAdjacent(v);  //取当前顶点v的邻接顶点

        //判断顶点v有没有邻接顶点-----有：指向递归循环深度遍历算法
        for(int i=0; i<aj->length(); i++)  
        {
            if( !visited[(*aj)[i]] )    //当前邻接顶点没有被访问
            {
                DFS(g, (*aj)[i], visited);    //递归深度优先遍历  ---以邻接顶点为起始顶点 ，遍历图
            }
        }
    }
    else
    {
        THROW_EXCEPTION(InvalidParameterException, "Index v is invalid...");
    }
}

//二叉树先序遍历图 
template < typename V, typename E >   //g 深度遍历的图  v 图的顶点
void DFS(Graph<V, E>& g, int v)
{
    DynamicArray<bool> visited(g.vCount());   //标记数组 ---- 标记顶点是否被访问

    for(int i=0; i<visited.length(); i++)  //每个元素顶点设置为未访问状态
    {
        visited[i] = false;
    }

    DFS(g, v, visited);   //触发递归函数
}

int main()
{
    MatrixGraph<9, char, int> g;
    const char* VD = "ABEDCGFHI";

    for(int i=0; i<9; i++)
    {
        g.setVertex(0, VD[i]);
    }

    g.setEdge(0, 1, 0);
    g.setEdge(1, 0, 0);

    g.setEdge(0, 3, 0);
    g.setEdge(3, 0, 0);

    g.setEdge(0, 4, 0);
    g.setEdge(4, 0, 0);

    g.setEdge(1, 2, 0);
    g.setEdge(2, 1, 0);

    g.setEdge(1, 4, 0);
    g.setEdge(4, 1, 0);

    g.setEdge(2, 5, 0);
    g.setEdge(5, 2, 0);

    g.setEdge(3, 6, 0);
    g.setEdge(6, 3, 0);

    g.setEdge(4, 6, 0);
    g.setEdge(6, 4, 0);

    g.setEdge(6, 7, 0);
    g.setEdge(7, 6, 0);

    g.setEdge(7, 8, 0);
    g.setEdge(8, 7, 0);

    SharedPointer< Array<int> > sa = g.DFS(0); 

    for(int i=0; i<sa->length(); i++)
    {
        cout << (*sa)[i] << " ";
    }
 
    cout << endl;

    DFS(g, 0);  //递归版本

    return 0;
}

结果如下：

小结：

                     

              使用栈----------深度优先--------

               使用队列-------广度优先